
- •Вопросы экзамена по математическому анализу для студентов 1 курса экономического факультета анх
- •Вопрос 1: множества и операции над ними
- •Вопрос 2 : декартово произведение множеств, бинарные отношения
- •Вопрос 3: отображения и их свойства
- •Вопрос 4: множество действительных чисел. Аксиома отделимости
- •§1. Натуральные числа
- •§ 1΄. Аксиомы Пеано
- •§ 2. Целые числа
- •§ 3. Рациональные числа
- •§4. Действительные числа
- •Вопрос 5:верхняя и нижняя грани
- •2. Стягивающиеся отрезки
- •Вопрос 6. Предельные точки
- •Вопрос 7. Приближённые вычисления
- •Вопрос 8. Предел последовательности. Предел функции. Бесконечно малые величины .Арифметические свойства предела
- •Вопрос 9. Предельный переход в неравенствах. Вычисление
- •Вопрос 10: предел монотонной ограниченной функции
- •Вопрос 11: число e
- •Вопрос 12: критерий коши существования предела последовательности, предела функции
- •Вопрос 13: непрерывность. Точки разрыва.Свойства непрерывных функций
- •1. Непрерывна в точке ;
- •2. Существует такая , что.
- •Вопрос 14: непрерывность элементарных функций
- •Вопрос 15: символы ,. Вычисление ,,
- •Вопрос 16: промежуточные значения непрерывной на отрезке функции
- •Вопрос 17: ограниченность непрерывной на отрезке функции
- •Вопрос 18: равномерная непрерывность
- •Вопрос 19: производная, её естественнонаучный смысл и основные свойства
- •1. Дифференцируемость функции
- •2.Производная
- •3. Касательная к графику функции
- •4. Правила дифференцирования
- •4. Производная обратной функции
- •6. Производная сложной функции
- •7. Производная функции, заданной параметрически
- •Вопрос 20: дифференциал. Инвариантность формы первого дифференциала
- •1.Понятие дифференциала числовой функции
- •4.Дифференциал суммы, произведения и частного функций.
- •Вопрос 21:производные и дифференциалы высших порядков
- •1. Последовательные производные
- •2. Примеры
- •3. Линейное свойство производных высших порядков
- •Вопрос 22.
- •Вопрос 23: теоремы ферма, ролля. Необходимые условия экстремума
- •Вопрос 24:теоремы лагранжа, коши.Критерий постоянства функции
- •Вопрос 25: формула тейлора с остаточным членом в форме лагранжа
- •Вопрос 26. Формула тейлора с остаточным членом в форме пеано
- •Вопрос 28: правила лопиталя
- •1. Неопределённость типа
- •Вопрос 29: монотонность функции. Достаточные условия экстремума функции
- •Вопрос 30. Функции спроса торнквиста. Функция полезности. Выпуклость графикафункции.
- •2.Производственные функции.
- •5. Выпуклость графика функции.
- •Необязательный материал, но знание его весьма полезно
- •1.Выпуклость непрерывной функции
- •2. Выпуклость дифференцируемой функции
- •3. Выпуклость дважды дифференцируемой функции
- •4.Точки перегиба
- •31. Пространство , множества в нем.
- •Вопрос32.Функции и отображения. Предел, непрерывность.
- •Функции Кобба-Дугласа.
- •Вопрос 33. Дифференцируемость функции многих переменных. Частные производные
- •Вопрос 34.
- •Вопрос 35.
- •Производная сложной функции. Инвариантность формы первого дифференциала.
- •Вопрос 36. Касательная плоскость
- •Вопрос 37. Производная по направлению, градиент.
- •Необязательный материал, но знание его весьма полезно Матрица Якоби и ее свойства.
- •Вопрос 39. Производные высших порядков
- •Дифференциалы высших порядков
- •Второй дифференциал функции.
- •Вопрос 41. Формулы Тейлора.
- •Билет 42. Экстремумы функций нескольких переменных.
- •Достаточные условия экстремума.
- •Метод наименьших квадратов.
Метод наименьших квадратов.
В различных исследованиях приходится пользоваться формулами, составленными на основании эксперимента. Одним из лучших способов получения формул является метод наименьших квадратов.
Пусть на основании эксперимента необходимо установить функциональную зависимость между переменными величинами x и y , например, между температурой и удлинением прямолинейного металлического стержня. Производим n измерений, по результатам составляем таблицу
|
X |
x1 |
x2 |
… |
xi |
… |
xn |
|
Y |
y1 |
y2 |
… |
yi |
… |
yn |
При
этом вид функции
![]() устанавливается из теоретических
исследований, или по характеру положения
на координатной плоскости экспериментальных
точек. Пусть, например, точки, взятые из
таблицы, расположены так, как показано
на рис. 45. В данном случае естественно
предположить, что между
устанавливается из теоретических
исследований, или по характеру положения
на координатной плоскости экспериментальных
точек. Пусть, например, точки, взятые из
таблицы, расположены так, как показано
на рис. 45. В данном случае естественно
предположить, что между
![]() и
и
![]() существует линейная зависимость,
выражающаяся формулой
существует линейная зависимость,
выражающаяся формулой
![]() (1)
(1)
Мы ограничимся рассмотрением случая линейной зависимости.
Так
как точки (x1;y1),(x2;y2),…,(xn;yn)
приблизительно лежат на одной прямой,
то формула (1) является приближенной.
Поэтому, подставляя их координаты в
формулу (1) вместо
![]() и
и
![]() получим следующие равенства:
получим следующие равенства:
![]() ,
,
![]() ,
………………,
,
………………,
![]() .
.
где
![]() некоторые числа, которые назовем
погрешностями.
некоторые числа, которые назовем
погрешностями.
Возникает
задача – подобрать коэффициенты
![]() таким образом, чтобы эти погрешности
были возможно, меньше по абсолютной
величине. Методом решения этой задачи
и является метод
наименьших квадратов.
Согласно этому методу рассмотрим сумму
квадратов погрешностей:
таким образом, чтобы эти погрешности
были возможно, меньше по абсолютной
величине. Методом решения этой задачи
и является метод
наименьших квадратов.
Согласно этому методу рассмотрим сумму
квадратов погрешностей:
![]() .
.
где
![]() и
и
![]() - заданные числа, а коэффициенты
- заданные числа, а коэффициенты
![]() –
неизвестные величины, подлежащие
определению, т.е.
–
неизвестные величины, подлежащие
определению, т.е.
![]() можно рассматривать как функцию двух
переменных
можно рассматривать как функцию двух
переменных
![]() и исследовать ее на экстремум.
и исследовать ее на экстремум.
Имеем
![]() ,
,
![]() .
.
П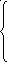 риравнивая
эти частные производные нулю, получаем
линейную систему двух уравнений с двумя
неизвестными
риравнивая
эти частные производные нулю, получаем
линейную систему двух уравнений с двумя
неизвестными
![]() :
:
![]()
![]() (2)
(2)
Система
(2) называется нормальной системой метода
наименьших квадратов. Из нее мы находим
числа
![]() ,
подставляя их в уравнение (1), получаем
форму искомой прямой.
,
подставляя их в уравнение (1), получаем
форму искомой прямой.
Во – первых, для разрешимости системы (2) потребуется условие
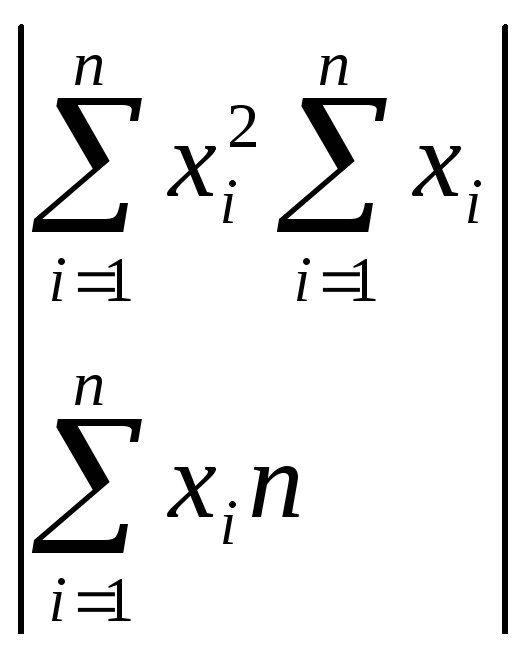 =
=![]()
![]() (3)
(3)
Лемма.
Величина
в правой части (3) равна
![]() и, следовательно, больше
0.
и, следовательно, больше
0.
Доказательство.
Правая часть этого равенства равна
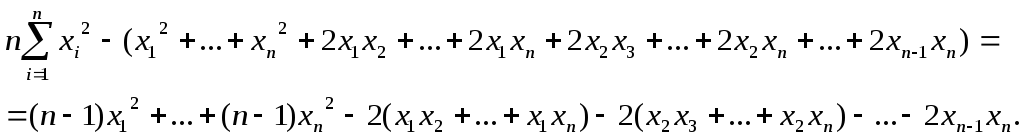
Эту
сумму легко сгруппировать и получить
![]() .
.
Итак,
такие a,
b
, чтобы выполнялась система (2), существуют.
Чтобы проверить, что в этих точках
функция S(a,b)
действительно имеет минимум, вычислим
![]()
![]() .
Следовательно, определитель
.
Следовательно, определитель
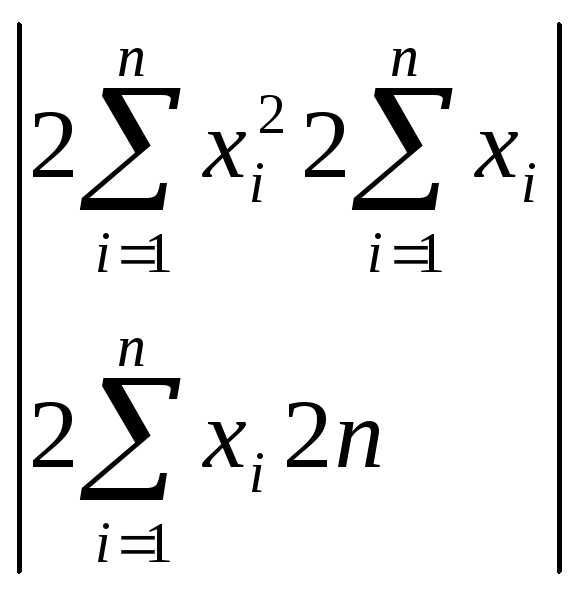 ,
по лемме
имеет
положительные главные миноры, поэтому
найденная точка – точка минимума.
,
по лемме
имеет
положительные главные миноры, поэтому
найденная точка – точка минимума.
Пример.
Пусть в результате эксперимента получены
пять значений искомой функции у при
пяти значениях аргумента х (n=5),
которые записаны в таблице: ![]()
![]()
![]()
![]()
![]()
![]() дем
искать функциональную зависимость
между x
и y
в виде линейной функции y=ax+b.
дем
искать функциональную зависимость
между x
и y
в виде линейной функции y=ax+b.
При составлении нормальной системы (2) для определения коэффициентов a и b, вычисляем
![]()
Система (2) принимает вид
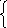 25a+5b=16,5,
25a+5b=16,5,
5a+5b=8.
Решая эту систему, находим: a=0,425,b=1,175. Отсюда формула искомой прямой есть
y=0,425x+1,175.
