5. Выпуклость графика функции.

Пусть Тогда в каждой точке её графика есть касательная, уравнение которой:

Определение. Функция называется выпуклой вниз на (a,b), если (т.е точка графикалежит над касательной к этому графику в любой точке)

Выпуклость вверх определяется условием:

Теорема1. Если производная - возрастающая на (a,b) функция, то - выпуклая вниз на (a,b)

►=, гдележит междуиx , по теореме Лагранжа, все условия которой, разумеется, выполнены.

Пусть . Тогда>0 и, поэтому-

Если же ., то<0,и снова-◄

Аналогично доказывается, что если удовлетворяет на (a,b), то график - выпуклая вверх функция.

Примером служит функция полезности, полезность продукта с ростом насыщения падает, что означает выпуклость графика этой функции вверх.

Если имеет вторую производную на (a,b), то из теоремы 1 следует:

Если >0 на (a,b), то график функции выпуклый вниз, если <0 - то вверх.

В качестве примера рассмотрите и

Точка, в которой направление выпуклости меняется на противоположное, называется точкой перегиба. Если существует то, поскольку в точке перегибапроизводная имеет экстремум, в ней вторая производная равна 0, т.е.

Например, имеет в =0 перегиб, так как слева от=0 т.е приx<0, <0, и приx>0, >0.

В самой точке =0=0

Разумеется, равенство - это необходимое условие точки перегиба. Оно не является достаточным, как показывает пример функции . Она имеет вторую производную , которая не меняет знак, но обращается в 0 в точке=0. Эта функция выпукла вниз наR.

Достаточное условие точки перегиб даёт такое утверждение:

Пусть непрерывны на (a.b) и пусть в точке выполнены условия:.

Тогда если n – нечётное число, то - точка перегиба, еслиn – чётное число, то в нет перегиба.

Для доказательства используем формулу Тейлора с остаточным членом в форме Пеано:

- , гдепри

Из условий следует, что

-

Рассуждая, как в случае вопроса о точках экстремума, получаем, что знак первой части совпадает со знаком , еслиn – чётное число, и меняется, если n – нечётное число (при x из окрестности точки ) Это доказывает утверждение.

Необязательный материал, но знание его весьма полезно

1.Выпуклость непрерывной функции

Определение 30.1. Непрерывная на интервале (a,b) функция f , называется выпуклой вниз (соответственно, выпуклой вверх), если для любых точек ,, и любого числасправедливо неравенство

(1)

(соответственно, неравенство

. (1’)

В правой части неравенства (1) стоит значение функции f в произвольной точке , расположенной на отрезке, содержащемся в интервале(a,b). Левая часть в (1) выражает собой ординату точки координатной плоскости, абсцисса которой равна ,, и которая лежит на прямолинейном отрезке (хорде), соединяющем точкииграфика функцииf.

Итак, если непрерывная функция f выпукла вниз на интервале (a,b), то для любых его точек ,, график функции f на отрезке расположен ниже хорды, стягивающей концевые точки графика на этом отрезке (см. рис.1, а)).

Рис.1

Аналогично, заключаем, что если непрерывная функция f выпукла вверх на интервале (a,b), то для любых его точек ,, график функции f на отрезке расположен выше хорды, стягивающей концевые точки графика на этом отрезке (см. рис.1,b)).

Обозначим . Тогда, откуда.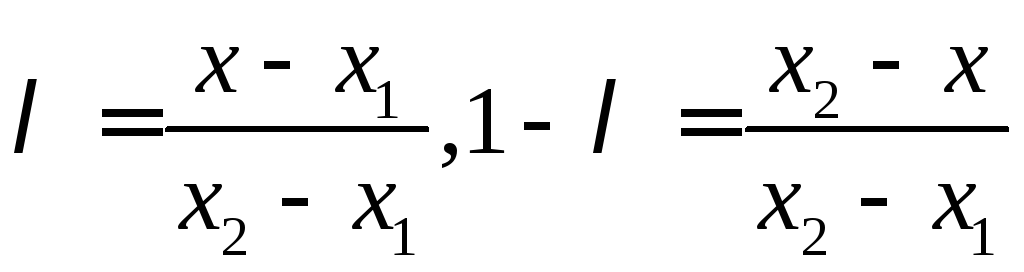

Неравенство (1) принимает вид

, (2)

или, после умножения обеих частей его на множитель ,

. (3)

Поскольку , то после элементарных преобразований неравенство (4) переходит в неравенство

, (4)

справедливое для любого .

Итак, условие (1) равносильно неравенству (4).

В случае выпуклости вверх знаки неравенств (2)-(4) следует сменить на противоположные.