Вопрос 26. Формула тейлора с остаточным членом в форме пеано

Теорема 26.1 (Формула Тейлора с остаточным членом в форме Пеано (G.Peano)). Пусть в окрестности точкисуществуют и непрерывны, …. Пустьсуществует ви непрерывна в точке

Тогда 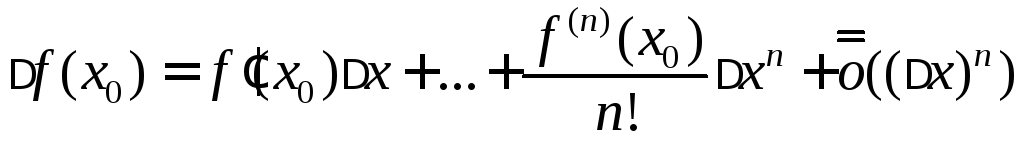при(1)

◄Используем предыдущую теорему, в которой число заменим числом. Тогда

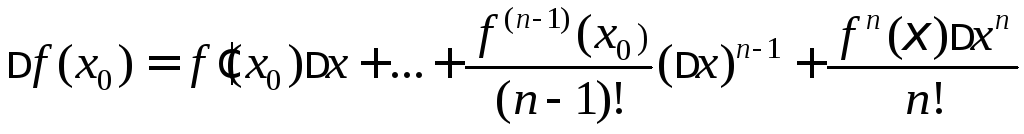, где – междуи . (2)

При как, так и заключённое междуи число стремятся к. Ввиду непрерывностив точке,, гдепри, т.е. при.

Подставляя в (2), получаем:

,

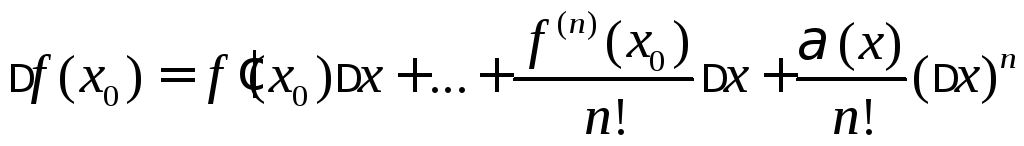где при, откуда сразу следует заключение теоремы. ►

Замечание. Вместо формул (7) и (8) предыдущего параграфа имеем, соответственно, 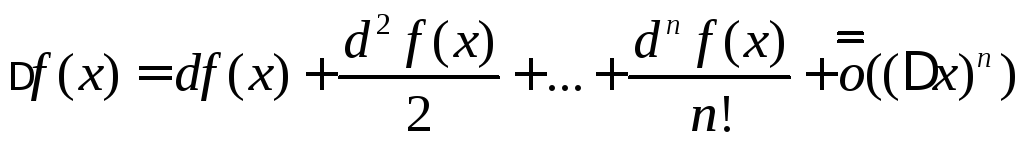при. И

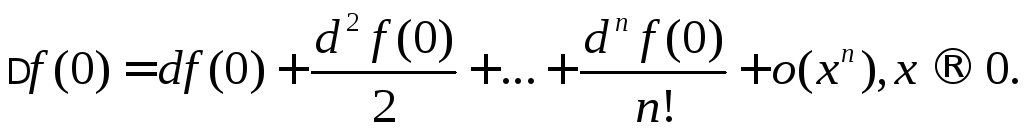
Замечание. Утверждение теоремы останется справедливым, если предположить, что в окрестности точкисуществуют и непрерывны, …и что существует.

На экзамене это доказывать не требуется, однако ниже приведено доказательство этого утверждения – для тех, кому это интересно.

Доказать его легче всего используя правило Лопиталя (вопрос28).

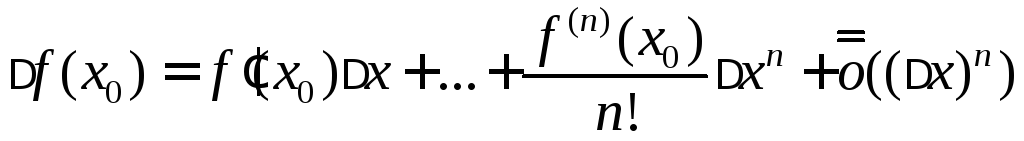Теорема 26.2. +28.5. Пусть в окрестности точкисуществуют и непрерывны, …и пусть существует. Тогдапри.

◄ Обозначим 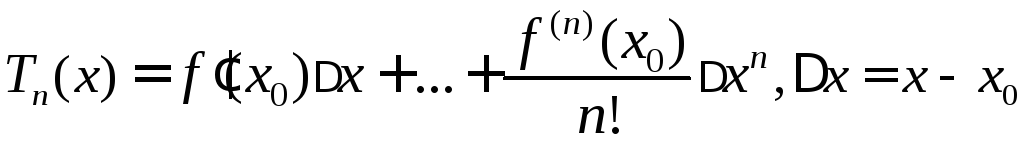,и рассмотрим отношение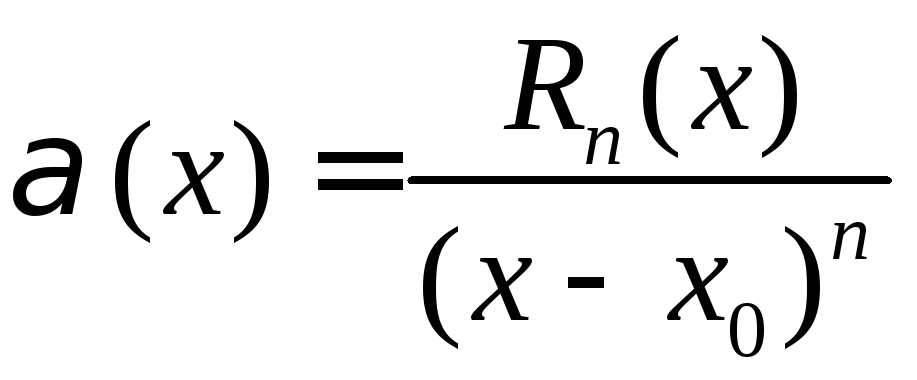. По правилу Лопиталя( теореме 28.1), применённомураз, имеем

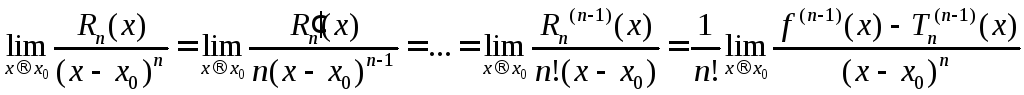.Из определения следует, что .Поэтому

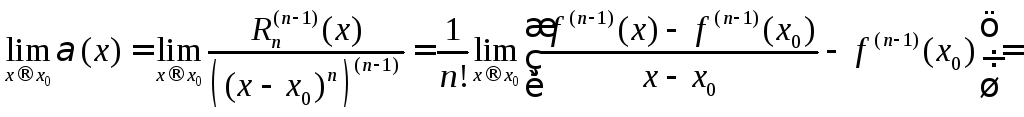
.Это означает, что =, что и требовалось доказать.►

Вопрос 27. РАЗЛОЖЕНИЯ ФУНКЦИЙ e^x, sinx, cosx, lnx, (1+x)^µ

Применим доказанные формулы Тейлора к функциям, перечисленным выше.

1) Так как , для всехвыполняется равенство

.Следовательно, все эти производные равны 1 при x=0.

Поэтому , где ξ – некоторая точка между 0 иx. Другая запись для точки ξ : ξ = θ x, 0 <  <1. Это – разложение e^x с остаточным членом в форме Лагранжа.

Формула Тейлора с остаточным членом в форме Пеано для e^x принимает вид ,.

2)Перейдём к функциям sinx, cosx:

, , , и т.д.

Эти равенства означают, что для любого . Поэтому имеет место формула , которую легко проверить для n=0,1,2,3, а для остальных n она верна ввиду установленного равенства .

Поэтому при x=0 имеем: производная порядка 4k равна ; производная порядка 4k+1 равна ; производная порядка 4k+2 равна ; производная порядка 4k+2 равна .

Следовательно, 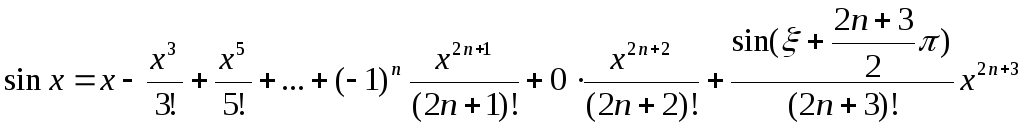, где ξ лежит между 0 иx. Здесь – небольшая хитрость. Мы разложили функцию до членов степени 2n+2 , что позволило сделать погрешность меньшей. Конечно, член выписывать не надо, он равен 0, а здесь он был помещён только для разъяснения вышеупомянутой «хитрости». Итак.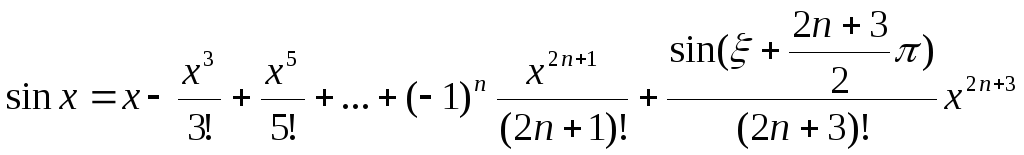

Аналогично, и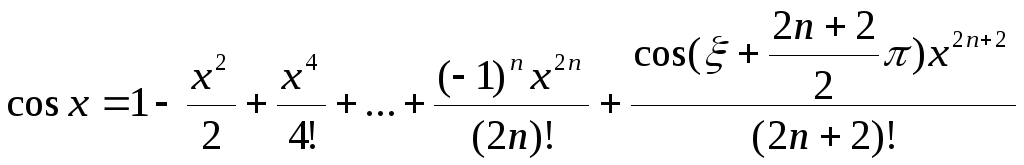

Разложения для sinx и cosx по формуле Тейлора с остаточным членом в форме Пеано имеют вид:

, x→0

, x→0

3)Перейдём к функции . Её последовательные производные равны:

,

и т.д.

Вычисленная при х=0, производная порядка k равна

Поэтому

,

где ξ – некоторая точка между 0 и х.

Разложение с остаточным членом в форме Пеано имеет вид:

4)Наконец, вычислим последовательные производные функции :

, ,,.

Вычисленная в точке , производная порядкаравна.

Поэтому формула Тейлора с остаточным членом в форме Лагранжа имеет вид:

,

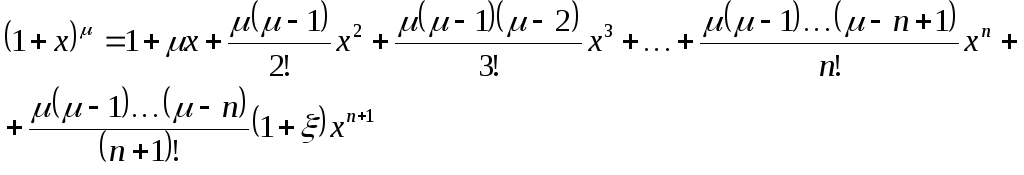где - междуи. Это так называемоебиноминальное разложение с остаточным членом в форме Лагранжа. Та же формула с остаточным членом в форме Пеано имеет вид:

, .

В качестве примера применения формулы Тейлора рассмотрим задачу нахождения с точностью до 0,001.

Сначала подготовим ее к применению формулы Тейлора. Для этого, зная, что , перепишем вычисляемую величину в виде.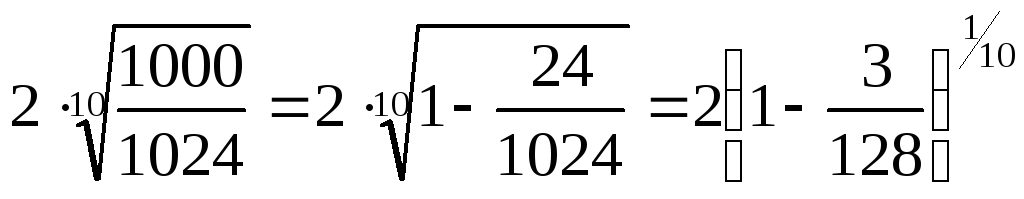

Используем биноминальное разложение при

, .

Число членов разложения выберем, исходя из заданной точности. Для этого найдем такое, чтобы:

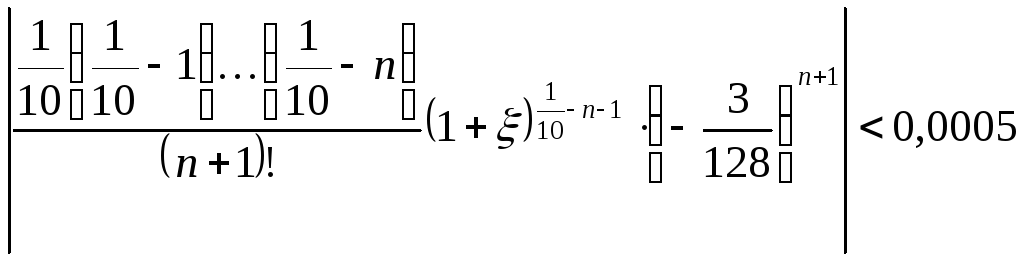(1)

(тогда при умножении на стоящий впереди коэффициент 2 получаем требуемую точность 0,001).

Очевидно, что:

;

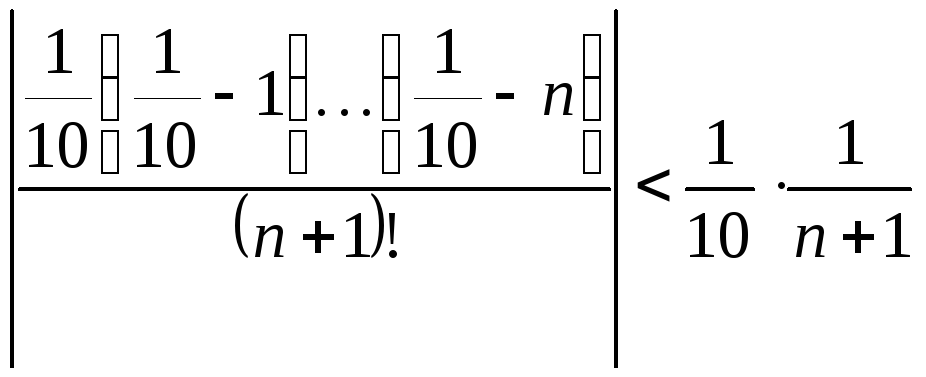Далее, - междуи, поэтомуи,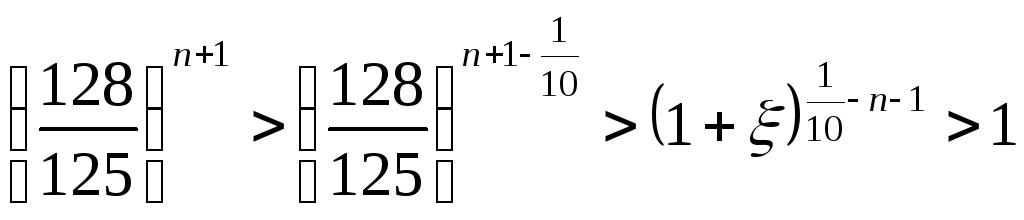

поэтому

Итак, абсолютная величина левой части неравенства (1) не больше, чем

. (2)

Поэтому если число (2) окажется меньше, чем 0,0005, то и остаточный член формулы будет меньше 0,0005 и требуемая точность будет достигнута.

Сразу ясно, что при

Число .

Поэтому требуемую точность для приближенной величины даёт приближённая формула:

.