
- •Вопросы экзамена по математическому анализу для студентов 1 курса экономического факультета анх
- •Вопрос 1: множества и операции над ними
- •Вопрос 2 : декартово произведение множеств, бинарные отношения
- •Вопрос 3: отображения и их свойства
- •Вопрос 4: множество действительных чисел. Аксиома отделимости
- •§1. Натуральные числа
- •§ 1΄. Аксиомы Пеано
- •§ 2. Целые числа
- •§ 3. Рациональные числа
- •§4. Действительные числа
- •Вопрос 5:верхняя и нижняя грани
- •2. Стягивающиеся отрезки
- •Вопрос 6. Предельные точки
- •Вопрос 7. Приближённые вычисления
- •Вопрос 8. Предел последовательности. Предел функции. Бесконечно малые величины .Арифметические свойства предела
- •Вопрос 9. Предельный переход в неравенствах. Вычисление
- •Вопрос 10: предел монотонной ограниченной функции
- •Вопрос 11: число e
- •Вопрос 12: критерий коши существования предела последовательности, предела функции
- •Вопрос 13: непрерывность. Точки разрыва.Свойства непрерывных функций
- •1. Непрерывна в точке ;
- •2. Существует такая , что.
- •Вопрос 14: непрерывность элементарных функций
- •Вопрос 15: символы ,. Вычисление ,,
- •Вопрос 16: промежуточные значения непрерывной на отрезке функции
- •Вопрос 17: ограниченность непрерывной на отрезке функции
- •Вопрос 18: равномерная непрерывность
- •Вопрос 19: производная, её естественнонаучный смысл и основные свойства
- •1. Дифференцируемость функции
- •2.Производная
- •3. Касательная к графику функции
- •4. Правила дифференцирования
- •4. Производная обратной функции
- •6. Производная сложной функции
- •7. Производная функции, заданной параметрически
- •Вопрос 20: дифференциал. Инвариантность формы первого дифференциала
- •1.Понятие дифференциала числовой функции
- •4.Дифференциал суммы, произведения и частного функций.
- •Вопрос 21:производные и дифференциалы высших порядков
- •1. Последовательные производные
- •2. Примеры
- •3. Линейное свойство производных высших порядков
- •Вопрос 22.
- •Вопрос 23: теоремы ферма, ролля. Необходимые условия экстремума
- •Вопрос 24:теоремы лагранжа, коши.Критерий постоянства функции
- •Вопрос 25: формула тейлора с остаточным членом в форме лагранжа
- •Вопрос 26. Формула тейлора с остаточным членом в форме пеано
- •Вопрос 28: правила лопиталя
- •1. Неопределённость типа
- •Вопрос 29: монотонность функции. Достаточные условия экстремума функции
- •Вопрос 30. Функции спроса торнквиста. Функция полезности. Выпуклость графикафункции.
- •2.Производственные функции.
- •5. Выпуклость графика функции.
- •Необязательный материал, но знание его весьма полезно
- •1.Выпуклость непрерывной функции
- •2. Выпуклость дифференцируемой функции
- •3. Выпуклость дважды дифференцируемой функции
- •4.Точки перегиба
- •31. Пространство , множества в нем.
- •Вопрос32.Функции и отображения. Предел, непрерывность.
- •Функции Кобба-Дугласа.
- •Вопрос 33. Дифференцируемость функции многих переменных. Частные производные
- •Вопрос 34.
- •Вопрос 35.
- •Производная сложной функции. Инвариантность формы первого дифференциала.
- •Вопрос 36. Касательная плоскость
- •Вопрос 37. Производная по направлению, градиент.
- •Необязательный материал, но знание его весьма полезно Матрица Якоби и ее свойства.
- •Вопрос 39. Производные высших порядков
- •Дифференциалы высших порядков
- •Второй дифференциал функции.
- •Вопрос 41. Формулы Тейлора.
- •Билет 42. Экстремумы функций нескольких переменных.
- •Достаточные условия экстремума.
- •Метод наименьших квадратов.
3. Линейное свойство производных высших порядков
Теорема
21.1. Для
любого числа
![]() ,
любых функцийu
и v,
имеющих в какой-то точке x
производные u(n)(x)
и v(n)(x),
и для любых чисел λ1,λ2
,
любых функцийu
и v,
имеющих в какой-то точке x
производные u(n)(x)
и v(n)(x),
и для любых чисел λ1,λ2![]()
![]() ,
функцияw
= λ1u
+ λ2v
имеет в точке x
производную w(n)(x)
и w(n)(x)
= (λ1u(x)
+ λ2v(x))(n)
= λ1u(n)(x)
+ λ2v(n)(x).
,
функцияw
= λ1u
+ λ2v
имеет в точке x
производную w(n)(x)
и w(n)(x)
= (λ1u(x)
+ λ2v(x))(n)
= λ1u(n)(x)
+ λ2v(n)(x).
◄ Поскольку каждая производная высшего порядка получается из производной предыдущего порядка посредством операции дифференцирования, а операция дифференцирования и первая производная обладают свойством линейности, то это свойство переносится на производные всех порядков.►
4. n-я производная произведения
Теорема
21.2.(Г. Лейбниц). Если
функции
f
и g
на некотором промежутке имеют производные
функции f(n)
и g(n),
n![]() ,
то существует (fg)(n)
и
,
то существует (fg)(n)
и
(fg)(n)
=
![]() = fg(n)
+ nf´g(n-1)
+ … +
= fg(n)
+ nf´g(n-1)
+ … +
![]() f(k)g(n-k)
+ … + nf(n-1)g´
+ f(n)g.
(1)
f(k)g(n-k)
+ … + nf(n-1)g´
+ f(n)g.
(1)
![]() Для
n=1
утверждение справедливо по теореме
19.8: вместе с f
и g
произведение fg
также дифференцируемо и
Для
n=1
утверждение справедливо по теореме
19.8: вместе с f
и g
произведение fg
также дифференцируемо и
(fg)´
= fg´ + f´g = C![]() f(0)g(1)
+ C
f(0)g(1)
+ C![]() f(1)g(0).
f(1)g(0).
Пусть
утверждение теоремы справедливо для
n,
а функции f
и g
(n+1)-кратно
дифференцируемы на рассматриваемом
промежутке.
Тогда эти функции вместе со своим
произведением n-кратно
дифференцируемы, и для него справедлива
формула (1). Так как в каждом члене правой
части этой формулы функции f(k)
и g(n-k)
дифференцируемы, то по теоремам 19.7, 19.8
функция (fg)(n)
дифференцируема, причем (fg)(n+1)
= ((fg)(n))´
=
![]() =
=
![]() .
.
Но
![]() =
=![]() и,
принимая также во внимание свойства
биномиальных коэффициентов:
и,
принимая также во внимание свойства
биномиальных коэффициентов:
![]() ,
получаем
,
получаем
(fg)(n+1)
=
![]() +
+
![]() +
+
![]() =
=
![]() ,
так что формула (1) верна, если заменить
n
на n+1
и теорема доказана.
,
так что формула (1) верна, если заменить
n
на n+1
и теорема доказана.
![]()
Вторая производная функции , заданной параметрически
Рассмотрим
уравнение ![]() (2)
(2)
Где
![]() ,
,![]() − дважды дифференцируемые функции на
некотором промежутке
− дважды дифференцируемые функции на
некотором промежутке![]() ;
пусть, кроме того, функция
;
пусть, кроме того, функция![]() строго возрастает (или убывает) на
строго возрастает (или убывает) на![]() и ни в одной точке этого промежутка
и ни в одной точке этого промежутка![]() не равна 0. В пункте 20.7 доказано, что в
этом случае уравнения (2) задают функцию
не равна 0. В пункте 20.7 доказано, что в
этом случае уравнения (2) задают функцию![]() ,
и производная этой функции равна
,
и производная этой функции равна
![]()
Бывает
также, что производные по параметру
![]() обозначают так:
обозначают так:![]() ,
,![]() .
Тогда формула (3)
принимает вид:
.
Тогда формула (3)
принимает вид:
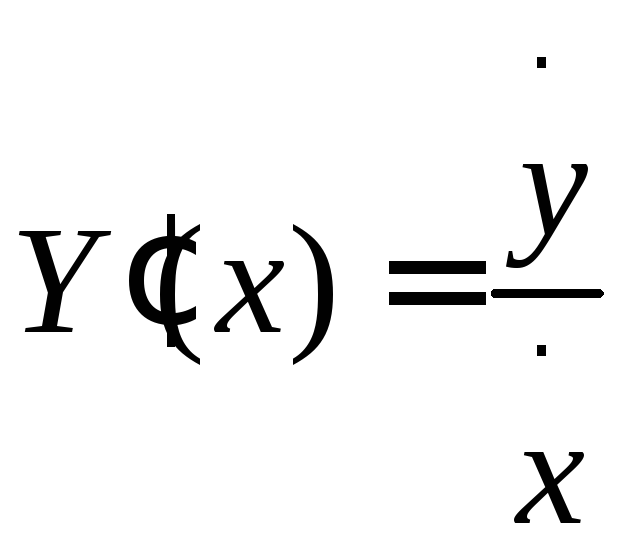 .
Найдём вторую производную функции
.
Найдём вторую производную функции
![]() :
:
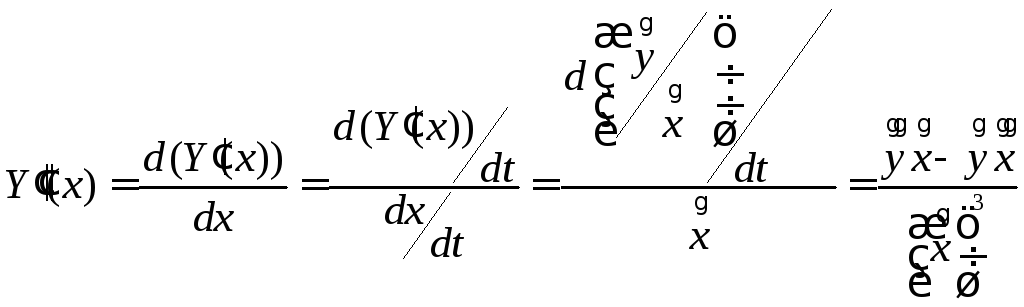
5.Дифференциалы высших порядков.
Однородную линейную функцию называют линейной формой.
Напомним,
что если функция
![]() дифференцируема в точке
дифференцируема в точке
![]() ,
то
,
то
дифференциалом
![]() в x
называют линейную форму
в x
называют линейную форму![]() .
.
Аналогично,
если
![]() дифференцируема
дважды в точке
дифференцируема
дважды в точке![]() ,
,
то
ее вторым
дифференциалом называют
квадратичную форму![]() .
.
Вообще,
n-ым
дифференциалом
![]() в точке x
будет n-ичная
в точке x
будет n-ичная
форма
![]() (в предположении, что
(в предположении, что
![]() существует).
существует).
Для
n-го
дифференциала
![]() в точке x
используют обозначение
в точке x
используют обозначение![]() или, более
или, более
строго
![]() .
.
Таким образом, по определению,
![]() =
=
![]() для
всех
для
всех
![]()
![]() .
(2)
.
(2)
Согласно
этому определению,
![]() есть
n-я
степень функции
есть
n-я
степень функции
![]() и
и
потому
используют обозначение
![]() .
Тогда (2) примет вид
.
Тогда (2) примет вид
![]() для
всех
для
всех
![]()
![]() ,
или равенства
,
или равенства
![]() .
(3)
.
(3)
Форма (2) записи n-го дифференциала не инвариантна
уже
при n=2.
Действительно, подставляя вместо
![]() дифференцируемую
дифференцируемую
функцию
![]() в
левую часть формулы (2) (при n=2),
получим
в
левую часть формулы (2) (при n=2),
получим
![]()
=![]() (4)
(4)
а в результате такой же подстановки в правую часть, имеем
![]() .(5)
.(5)
Правые
части формул (5) и (4) отличаются слагаемым
![]() .
.
Вообще
говоря, это слагаемое не равно нулю.
Однако если
![]() -
линейная функция,
-
линейная функция,
то
![]() и,
вообще, для любого
и,
вообще, для любого
![]() имеет место равенство
имеет место равенство![]() ,
,
откуда
следует, что формула (3) будет верна и
для линейной функции
![]() .
.
