4. Производная обратной функции

Прежде чем заняться вычислением производных от обратных тригонометрических функций, докажем следующую общую теорему.

Теорема 20.1.Пусть 1) функция возрастает(или убывает) и непрерывна на некотором промежутке 2) в точкеэтого промежутка имеетконечную и отличную от нуля производную . Тогда для обратной функциив соответствующей точкетакже существует производная, равная.

◄Придадим значению произвольное приращение, тогда соответственное приращениеполучит и функция. Заметим, что при, ввиду однозначности самой функции, и. Имеем

.

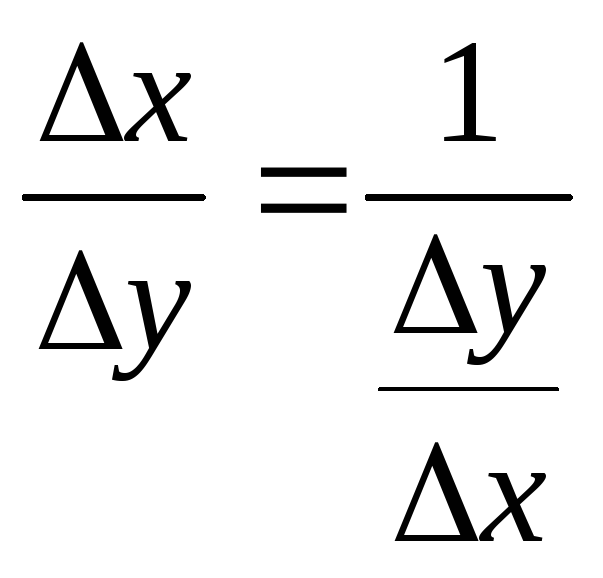Если теперь по любому закону, то − в силу непрерывности функции− и приращение. Но тогда знаменатель правой части написанного равенства стремится к пределу, следовательно, существует предел для левой части, равный обратной величине; он и представляет собой производную.►

Итак, имеем простую формулу:

.

Л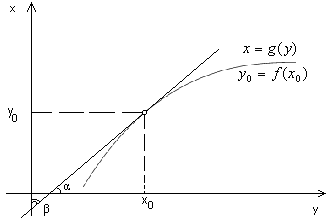егко выяснить еёгеометрический смысл. Мы знаем, что производная есть тангенс угла, образованный касательной к графику функциис осью. Но обратная функцияимеет, лишь независимая переменная для неё откладывается по оси. Поэтому производнаяравна тангенсу угла β, составленного той же касательной с осью(см. рис.) Таким образом, выведенная формула сводится к известному соотношению

,

связывающему тангенсы двух углов α и β, сумма которых равна .

Положим для примера . Обратной для неё функцией будет. Так как, то по нашей формуле,

,

в согласии с 3.

Переходя теперь к вычислению производных от обратных тригонометрических функций, мы для удобства обменяем ролями переменные x и y, переписав доказанную формулу в виде

.

5.Обратные тригонометрические функции. Рассмотрим функцию (), причем. Она является обратной для функции, имеющей для указанных значенийположительную производную. В таком случае существует также производнаяи равна, по нашей формуле,

;

корень мы берем со знаком плюс, так как .

Мы исключили значения , ибо для соответствующих значенийпроизводная.

Функция () служит обратной для функций. По нашей формуле

.

Аналогично можно получить:

для ()

для ().

6. Производная сложной функции

Теорема.(Теорема о производной сложной функции). Пусть функция определена в окрестности точкии имеет в этой точке производную. Пусть функцияопределена в окрестностии имеет в точкепроизводную

Тогда сложная функция имеет производную, равную

.

► Придадим приращениетакое, что соответствующее значениепринадлежит окрестности точки, в которой определена функция. Так как, по условию, дифференцируема в точке,

, где прии.

Так как дифференцируема в точке,

,где . Как установлено в теореме 19.1, если, то и.

Поэтому

Так как при и,,−бесконечно малые, из этого равенства следует, что

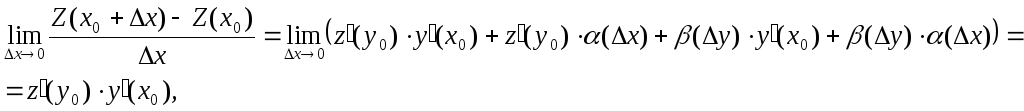что и требовалось доказать.►

7. Производная функции, заданной параметрически

Рассмотрим уравнение (1)

Где ,− дифференцируемые функции на некотором промежутке; пусть, кроме того, функциястрого возрастает (или убывает) наи ни в одной точке этого промежуткане равна 0.

Символ использован здесь для обозначения производной функциипо переменной. Тогда, по теореме 17.4, существует обратная функция, причем ее производная, по теореме20.1, равна

Но тогда уравнения задают , и производная этой функции, по теореме20.2 о производной сложной функции. Используя равенство (2), окончательно получаем:

Часто вместо равенства (3) записывают равносильное ему равенство

Бывает также, что производные по параметру обозначают так:,. Тогда формула (3) принимает вид: .
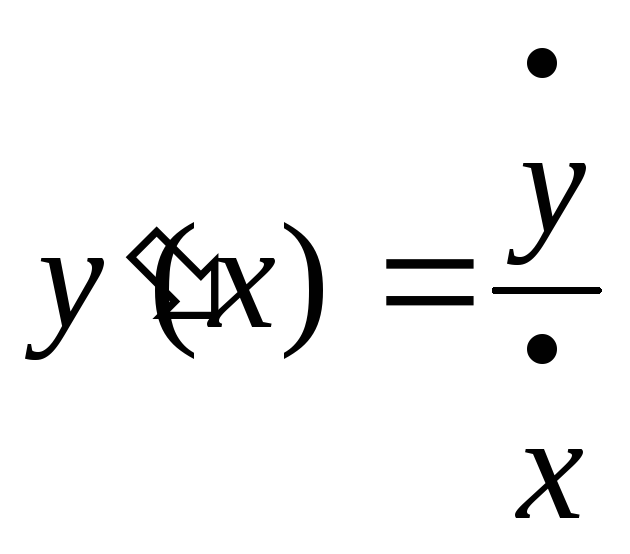