Вопрос 17: ограниченность непрерывной на отрезке функции

Теорема 17.1.(Вейерштрасс) Пусть функция непрерывна на отрезке. Тогда она ограничена на этом отрезке.

 Будем вести доказательство теоремы методом «от противного». Предположим, что не ограничена на отрезке . Это означает, что для любого числасуществует точкатакая, что. Последовательно выбирая числоравным числам, находим соответствующие точкитакие, что. Эти точки образуют бесконечную последовательность, а так как все они принадлежат отрезку, т.е., эта последовательность является ограниченной. Применяем теорему Больцано-Вейерштрасса для последовательностей, согласно которой существует подпоследовательностьпоследовательности, сходящаяся к некоторому пределу, который будем обозначать. Так как, по теореме о предельном переходе в неравенствах получаем:, т.е.и, следовательно, функция непрерывна в этой точке. Но это означает, что для любой последовательности, в частности, и для последовательности , стремящейся к, последовательность соответствующих значенийдолжна стремиться к. Но, поэтому последовательностьстремится к. Получено противоречие с предположением о неограниченности на отрезке .

Замечание. Если функциянепрерывна на интервале, то она может быть неограниченной на этом интервале. Например, функцияна интерваленепрерывна. Однако для любого числаимеет место неравенство, откудаи значение этой функции в точкеравно.

Следствие. Пусть функция непрерывна на отрезке. Тогда существуют точная верхняя грань и точная нижняя грань множества её значений на отрезке .

 Достаточно применить к множеству значений функции на отрезкетеорему о существовании точных граней ограниченного множества.

Теорема 17.2.(Вейерштрасс) Пусть функция непрерывна на отрезке. Тогда существуют такие точки ,принадлежащие этому отрезку, что .

 Докажем часть утверждения теоремы, относящуюся к точной верхней грани множества значений функции на отрезке . Остальная часть доказывается аналогично.

Будем вести доказательство теоремы методом «от противного». Пусть для всех точек отрезкавыполняется неравенство. Тогдадля всех точекотрезкаи функцияопределена и непрерывна на отрезке. По теореме 17.1 эта функция ограничена на отрезке, следовательно, существует числотакое, что для всех точекотрезкавыполняются неравенства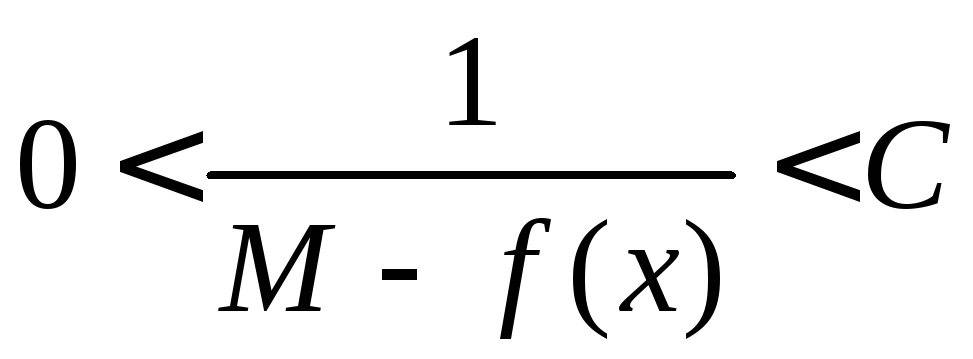. Но тогда для всех точекиз отрезкавыполняется неравенство, или. Это означает, что меньшее, чем, числоявляется верхней гранью множества значений функции на отрезке . Значит,- не точная верхняя грань множества значений функции на отрезке .

Замечание. Часто эту теорему формулируют так:

Непрерывная на отрезке функция принимает свои наименьшее и наибольшее значения на этом отрезке.

Следствие. Пусть функция непрерывна на отрезке. Тогда для любого числа, удовлетворяющего неравенствам, существует точкатакая, что.

 По доказанной теореме, существуют такие точки , принадлежащие отрезку, что. Рассмотрим отрезок числовой оси, соединяющий эти точки. Пусть, для определённости,. Тогда функция непрерывна на отрезке . По следствию теоремы 16.1, для любого, удовлетворяющего неравенствам ,существует точкатакая, что.

Замечание. Доказанные утверждения означают, что непрерывная на отрезке функция принимает на нём все свои значения, от наименьшего до наибольшего. Разумеется, таким свойством могут обладать не только непрерывные функции. Например, функция 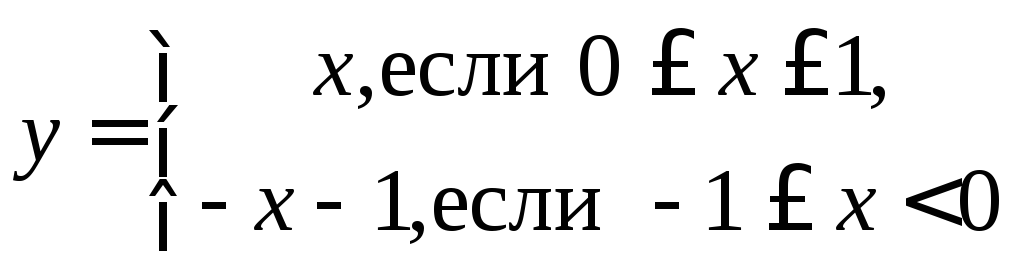принимает все значения от -1 до +1, однако имеет разрыв в точке.

Отметим ещё одно важное следствие теоремы 17.2.

Теорема 17.3. Пусть функция непрерывна на промежутке (конечном или бесконечном). Тогда множество её значений также представляет собой промежуток.

◄ Требуется доказать, что вместе с любыми двумя точками любая точка, также принадлежит . Пусть ,. Рассмотрим множество значений функции на отрезке (, т.к. -промежуток). Оно представляет собой отрезок, в котором содержится отрезок . Таким образом, любое числоявляется значениемдля некоторого . ►

Обратная функция

Обратная функция – частный случай понятия обратного отображения (см. определение 3.9). Если задана функция , обладающая тем свойством, что любое своё значение она принимает при единственном значении, то это даёт возможность рассматриватьобратную функцию , такую, что равенства и равносильны . Примером служат функции. Ясно, что обе функциональные зависимости, и определяют одну и ту же кривую на плоскости. Часто рассматривают функцию( и именно эту функцию называют обратной). График такой функции получается из графика функции отражением относительно биссектрисы первого координатного угла.

Теорема 17.4. Пусть функция возрастает (убывает) на промежутке . Тогда на промежутке , представляющем собой множество её значений (по теореме 17.3), определена обратная функция ,которая также возрастает(убывает) и непрерывна.

◄Ограничимся случаем возрастания. По определению множества значений функции, для любого существует числотакое, что. Так каквозрастает на , то для любого выполняется неравенство, а для любоговыполняется неравенство. Поэтому любое своё значениефункцияпринимает ровно один раз, в точке, что и позволяет определить функциютакую, что для любоговыполняется равенство. Легко видеть, функциявозрастает на . Действительно, как показано выше, для любого значениясоответствуют значениям, а значениясоответствуют значениям. Но это означает, что и обратно, для любогозначениясоответствуют значениям, а значениясоответствуют значениям. Наконец, для доказательства непрерывностина промежуткевоспользуемся теоремой 14.1. Действительно, функциявозрастает на промежуткеи её множество значений образует промежуток . ►