- •Вопросы экзамена по математическому анализу для студентов 1 курса экономического факультета анх
- •Вопрос 1: множества и операции над ними
- •Вопрос 2 : декартово произведение множеств, бинарные отношения
- •Вопрос 3: отображения и их свойства
- •Вопрос 4: множество действительных чисел. Аксиома отделимости
- •§1. Натуральные числа
- •§ 1΄. Аксиомы Пеано
- •§ 2. Целые числа
- •§ 3. Рациональные числа
- •§4. Действительные числа
- •Вопрос 5:верхняя и нижняя грани
- •2. Стягивающиеся отрезки
- •Вопрос 6. Предельные точки
- •Вопрос 7. Приближённые вычисления
- •Вопрос 8. Предел последовательности. Предел функции. Бесконечно малые величины .Арифметические свойства предела
- •Вопрос 9. Предельный переход в неравенствах. Вычисление
- •Вопрос 10: предел монотонной ограниченной функции
- •Вопрос 11: число e
- •Вопрос 12: критерий коши существования предела последовательности, предела функции
- •Вопрос 13: непрерывность. Точки разрыва.Свойства непрерывных функций
- •1. Непрерывна в точке ;
- •2. Существует такая , что.
- •Вопрос 14: непрерывность элементарных функций
- •Вопрос 15: символы ,. Вычисление ,,
- •Вопрос 16: промежуточные значения непрерывной на отрезке функции
- •Вопрос 17: ограниченность непрерывной на отрезке функции
- •Вопрос 18: равномерная непрерывность
- •Вопрос 19: производная, её естественнонаучный смысл и основные свойства
- •1. Дифференцируемость функции
- •2.Производная
- •3. Касательная к графику функции
- •4. Правила дифференцирования
- •4. Производная обратной функции
- •6. Производная сложной функции
- •7. Производная функции, заданной параметрически
- •Вопрос 20: дифференциал. Инвариантность формы первого дифференциала
- •1.Понятие дифференциала числовой функции
- •4.Дифференциал суммы, произведения и частного функций.
- •Вопрос 21:производные и дифференциалы высших порядков
- •1. Последовательные производные
- •2. Примеры
- •3. Линейное свойство производных высших порядков
- •Вопрос 22.
- •Вопрос 23: теоремы ферма, ролля. Необходимые условия экстремума
- •Вопрос 24:теоремы лагранжа, коши.Критерий постоянства функции
- •Вопрос 25: формула тейлора с остаточным членом в форме лагранжа
- •Вопрос 26. Формула тейлора с остаточным членом в форме пеано
- •Вопрос 28: правила лопиталя
- •1. Неопределённость типа
- •Вопрос 29: монотонность функции. Достаточные условия экстремума функции
- •Вопрос 30. Функции спроса торнквиста. Функция полезности. Выпуклость графикафункции.
- •2.Производственные функции.
- •5. Выпуклость графика функции.
- •Необязательный материал, но знание его весьма полезно
- •1.Выпуклость непрерывной функции
- •2. Выпуклость дифференцируемой функции
- •3. Выпуклость дважды дифференцируемой функции
- •4.Точки перегиба
- •31. Пространство , множества в нем.
- •Вопрос32.Функции и отображения. Предел, непрерывность.
- •Функции Кобба-Дугласа.
- •Вопрос 33. Дифференцируемость функции многих переменных. Частные производные
- •Вопрос 34.
- •Вопрос 35.
- •Производная сложной функции. Инвариантность формы первого дифференциала.
- •Вопрос 36. Касательная плоскость
- •Вопрос 37. Производная по направлению, градиент.
- •Необязательный материал, но знание его весьма полезно Матрица Якоби и ее свойства.
- •Вопрос 39. Производные высших порядков
- •Дифференциалы высших порядков
- •Второй дифференциал функции.
- •Вопрос 41. Формулы Тейлора.
- •Билет 42. Экстремумы функций нескольких переменных.
- •Достаточные условия экстремума.
- •Метод наименьших квадратов.
Вопрос 9. Предельный переход в неравенствах. Вычисление
Теорема
9.1.
Если
функция имеет предел при
![]() ,
равный А и в некоторой проколотой
окрестности
,
равный А и в некоторой проколотой
окрестности
![]() точки
a принимает неотрицательные значения,
то
точки
a принимает неотрицательные значения,
то
![]() .
.
Доказательство. Будем доказывать методом от противного.
Допустим,
что A<0. Возьмем
![]() .
Тогда
.
Тогда
![]()
![]()
![]()
![]() ,
откуда
,
откуда
![]()
Получаем,
что для любого
![]() из
пересечения проколотых окрестностей
из
пересечения проколотых окрестностей
![]() и
и
![]() одновременно
выполняются неравенства
одновременно
выполняются неравенства
![]() и
и![]() .
Тем самым мы пришли к противоречию.
Теорема доказана.
.
Тем самым мы пришли к противоречию.
Теорема доказана.
Теорема
9.2.Если
для двух функций
![]() и
и
![]() ,
имеющих пределы, соответственно,
,
имеющих пределы, соответственно,
![]() и
и
![]() ,
в некоторой проколотой окрестности
,
в некоторой проколотой окрестности
![]() выполняется
неравенство
выполняется
неравенство![]() ,
то
,
то
![]() .
.
Доказательство.
Обозначим
![]() .
При этом
.
При этом
![]()
![]()
![]() .
По теореме 9.1
имеем
.
По теореме 9.1
имеем
![]() ,
т.е.
,
т.е.
![]() .
Теорема доказана.
.
Теорема доказана.
Замечание:Эти две теоремы означают, что при переходе к пределу сохраняется нестрогое неравенство.
Замечание: строгое неравенство между функциями может не сохраниться для пределов.
Например,
для функций
![]() ,
,![]() в
любой
в
любой
![]() выполняется неравенство
выполняется неравенство![]() ,
т.е.
,
т.е.![]() .
Однако,
.
Однако,![]()
Теорема
9.3 (Теорема о “зажатой” переменной).
Если
![]() выполняется
неравенство
выполняется
неравенство![]() ,
и если
,
и если
![]() ,
то
,
то
![]()
Доказательство. Для доказательства данной теоремы докажем лемму:
Лемма
9.1. Если
![]() выполняется неравенство
выполняется неравенство![]() ,
и если
,
и если
![]() ,
то и
,
то и![]() .
.
Доказательство.
Требуется доказать, что:
![]()
![]()
![]()
![]()
![]() .
Имеется:
.
Имеется:
![]()
![]()
![]()
![]()
![]()
Выберем
![]() таким,
что
таким,
что![]() ,
а также удовлетворяющим неравенству
,
а также удовлетворяющим неравенству
![]() ,
из которого следует, что
,
из которого следует, что
![]() .Тогда
.Тогда
![]()
![]()
![]()
![]() ,
что означает, что
,
что означает, что
![]() .Лемма
доказана.
.Лемма
доказана.
Перейдем
к доказательству теоремы и обозначим
![]() .
При этом
.
При этом
![]() удовлетворяют
условиям леммы.
удовлетворяют
условиям леммы.
Далее,
![]() и,
по лемме,
и,
по лемме,
![]() .
Наконец,
.
Наконец,
![]() при
при
![]() (т.к.
(т.к.
![]() ,
,
![]() при
при
![]() ).
).
Таким образом, теорема доказана.
Определение
9.1. Если
![]()
![]()
![]()
![]()
![]() ,
то говорят, что существует предел
функции
,
то говорят, что существует предел
функции![]() при
стремлении х к а справа
и обозначают это так:
при
стремлении х к а справа
и обозначают это так:
![]() .
Аналогично, если
.
Аналогично, если
![]()
![]()
![]()
![]()
![]() ,
то говорят, что существуетпредел
функции
,
то говорят, что существуетпредел
функции![]() при
стремлении х к а слева
и обозначают это так:
при
стремлении х к а слева
и обозначают это так:
![]() .
.
Теорема
9.4. Функция
![]() имеетпри
имеетпри
![]() предел, равный а, тогда и только тогда,
когда он имеет пределы при стремлениих
к а справа и слева, причем оба эти пределы
равна А.
предел, равный а, тогда и только тогда,
когда он имеет пределы при стремлениих
к а справа и слева, причем оба эти пределы
равна А.
Доказательство
Если
![]() ,
то
,
то
![]()
![]()
![]()
![]()
![]() .
Поскольку из неравенств
.
Поскольку из неравенств![]() и
и
![]() следует
неравенство
следует
неравенство
![]() ,
,
![]() и
и![]() .
.
Обратно,
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]()
![]()
![]()
![]() ,
,![]() ;
;![]() тогда и только тогда, когда
тогда и только тогда, когда
![]()
![]()
![]()
![]() ,
,![]() .
.
Положим
![]() .
Тогда если
.
Тогда если
![]() ,
то
,
то
либо
![]() ,либо
,либо
![]()
И
в том, и в другом случае
![]() ,
т.е.
,
т.е.![]() .
.
Замечание. Разумеется, для пределов справа и слева верны все теоремы об арифметических свойствах предела и о предельном переходе в неравенствах.
Теорема 9.5 (первый замечательный предел)
![]() .
.
Замечание.
При доказательстве этой теоремы нельзя
применять правило Лопиталя, т.к. хотя
это и даст верный результат, но будет
являться логической ошибкой, потому,
что при вычислении производной функции
sinx
используется, что![]()
Доказательство
|
|
Функция
|
(В
определении требуется существование
хотя бы какого-нибудь
![]() .
Если же мы найдем
.
Если же мы найдем![]() ,
то, тем самым, хотя бы какое-нибудь
,
то, тем самым, хотя бы какое-нибудь![]() будет найдено.) Итак,
будет найдено.) Итак,![]() .
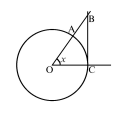
Рассмотрим окружность единичного
радиуса и площади треугольников OAC, OBC
и сектора OAC.
.
Рассмотрим окружность единичного
радиуса и площади треугольников OAC, OBC
и сектора OAC.![]() ,
,![]() ,
,![]()
![]() сект.
сект.![]() ,
откуда
,
откуда
![]() при
при
![]() ,
что равносильно
,
что равносильно
![]() ,
,
![]() .
Далее,
.
Далее,
![]() ,
а для
,
а для
![]() мы только что доказали, что
мы только что доказали, что![]() .
.![]() ,
поэтому по теореме9.3.
,
поэтому по теореме9.3.
![]() и,
значит,
и,
значит,![]() .
Снова применяем теорему9.3,
откуда
.
Снова применяем теорему9.3,
откуда
![]() и, значит,
и, значит,
![]() .
.