2.6. Определение вида закона распределения значений измеряемой величины

При обработке экспериментальных данных, а именно при определении выборочно среднего, дисперсии и доверительного интервала используется информация о виде закона распределения вероятности значений измеряемой величины.

Наиболее распространенным является случай нормального распределения, так как в большинстве реальных экспериментальных ситуаций справедлива центральная предельная теорема, из которой следует, что при достаточно больших объемах выборок распределение выборочных средних, полученное из различных исходных функций распределения, достаточно хорошо описывается нормальным распределением. Кроме того, многие практически важные распределения (Пирсона, Стьюдента и др.) уже при n>30 мало отличаются от нормального. В этом случае для обработки результатов используются стандартные (классические) статистические процедуры, рассмотренные в §2.3. Их недостаток состоит в том, что они весьма чувствительны к довольно малым отклонениям от предположений о нормальности, и если истинная функция распределения отличается от нормальной, то классические методы уже нельзя бездумно использовать. Поэтому появились так называемые робастные процедуры, т. е. нечувствительные к малым отклонениям от предположений. Приведем пример, показывающий к каким последствиям приводит отсутствие робастности по распределению в классических процедурах обработки [26].

Пример. Предположим, что имеется выборка объема n, составленная из большого числа “хороших” и “плохих” случайно перемешанных измерений xi некоторой величины m. Каждое “хорошее” измерение появляется с вероятностью 1–ε, а “плохое” – с вероятностью ε, где ε – малое число. Хорошие измерения xi имеют нормальное

распределение N (m,σ 2 ), плохие – нормальное распределение N (m,9σ 2 ).

Иными словами все значения имеют одно и то же среднее m, а стандартное отклонение для некоторых из них (плохих) в три раза больше

(дисперсия равна 9σ 2 ), чем у остальных (дисперсия равна σ2 ). Приведенная ситуация описывается следующим образом: величины xi независимы и имеют одно и то же распределение:

Рассмотрим две широко известные оценки разброса – среднее абсолютное отклонение:

dn = 1 ∑n x i − x

n i=1

(2.135)

и среднее квадратичное отклонение (СКО):

Известно, что для нормально распределенных измерений величина Sn примерно на 12% более эффективна, чем dn, однако на практике применение dn оказывается зачастую более правильным. Разумеется, величинами Sn и dn оцениваются разные характеристики распределения. Например, если измеренные значения имеют в точности нормальное распределение, то величина Sn сходится к σ, в то же время dn стремится к

π2σ ≈ 0,8σ . Поэтому следует уточнить, как проводить сравнение этих

оценок. Обычно используют так называемую асимптотическую относительную эффективность (АОЭ) оценки dn по оценке Sn,

где D(Sn), D(dn) – дисперсии, а E(Sn), E(dn) –математические ожидания соответствующих величин.

Значения этого показателя при различных ε приведены ниже:

Приведенные результаты показывают, что уже двух плохих наблюдений на тысячу (ε=0,002) достаточно, чтобы свести на нет 12%-ое преимущество среднеквадратичной оценки, причем наибольшее значение, которое показатель АОЭ(ε) принимает вблизи ε=0,05 превосходит 2.

Следует отметить, что типичные выборки ”хороших” данных довольно точно моделируются законом распределения (2.134); где ε меняется в пределах от 0,01 до 0,1. Приведенный пример убедительно показывает, что удлинение “хвостов” распределения ухудшает классическую оценку Sn и значительно меньше влияет на dn.

Иногда возникают экспериментальные ситуации, когда распределение неизвестно, т. е. может быть произвольным. В этом случае подход к обработке данных зависит от требований к точности результатов. При этом классическое оценки оказываются неэффективными, а иногда и просто не применимы (например, как уже отмечалось в §2.3. для распределения Коши математическое ожидание не определено, так как соответствующий интеграл расходится). Если требования к точности невысоки, то приемлемыми являются оценки, получаемые с использованием непараметрических критериев, например, знакоранговых или неравенства Чебышева. Однако, если требования к точности достаточно высокие, то информация о виде закона распределения является необходимой. Для определения вида закона распределения используются две группы методов: графические и аналитические. При использовании графических методов по имеющийся выборке объема n строится гистограмма (см. ниже), по виду гистограммы выдвигается гипотеза о законе распределения, а затем она проверяется по критериям согласия. В реальной ситуации, однако, редко получается “идеальная” форма гистограммы, так как она может маскироваться рядом факторов: интервал группирования данных, наличие ошибок и “плохих” данных и т. д. Поэтому принятие решения о законе распределения по виду гистограммы зачастую оказывается затруднительным или даже невозможным. На рис. 19 даны примеры наиболее типичных “неидеальных” гистограмм, встречающихся на практике [25].

1. Гребенка (мультимодальный тип). Классы через один имеют более низкие частоты. Такая форма встречается, когда число единичных наблюдений, попадающих в класс, колеблется от класса к классу или когда действует определенное правило

округления данных.

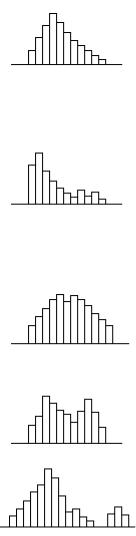
2. Положительно (отрицательно) скошенное распределение. Среднее значение гистограммы локализовано слева (справа) от центра размаха. Частоты довольно резко спадают при движении влево (вправо) и, наоборот, медленно вправо (влево). Форма

асимметрична. Такая форма встречается, когда нижняя (верхняя) граница регулируется либо теоретически, либо по значению допуска или когда левое (правое) значение недостижимо.

3. Распределение с обрывом слева (справа). Среднее арифметическое гистограммы локализуется далеко слева (справа) от центра размаха. Частоты резко спадают при движении влево (вправо), и, наоборот, медленно вправо (влево). Форма

асимметрична. Эта форма часто встречается при 100% просеивании изделий из-за плохой воспроизводимости процесса, а также, когда проявляется резко выраженная положительная (отрицательная) асимметрия.

4. Плато (равномерное и прямоугольное распределение). Частоты в разных классах образуют плато, так как все классы имеют более или менее одинаковые ожидаемые частоты. Эта форма встречается в смеси нескольких распределений, имеющих

разные средние.

5.Двухпиковый тип (бимодальный). В окрестностях центра диапазона данных частота низкая, зато есть по пику с каждой стороны. Эта форма встречается, когда смешиваются два распределения с далеко отстоящими средними значениями.

6.Распределение с изолированным пиком. Наряду с распределением обычного типа появляется изолированный пик. Эта форма появляется при наличии малых включений данных из другого распределения. Например, как в случае нарушения

нормального процесса, появления ошибки измерения или простого включения данных другого процесса.

Рис. 19. Типы “неидеальных” гистограмм, встречающихся на практике.

В этом случае чтобы избежать ошибки следует использовать аналитические методы, которые состоят в определении по выборке объема n оценок различных показателей формы эмпирического распределения: асимметрии, эксцесса, коэффициента формы распределения, контрэксцесса, энтропийного коэффициента и т. п. Найденные оценки сравниваются с допустимыми значениями показателей для теоретических законов распределения. Если оценки показателей формы эмпирического распределения, найденные по выборке, попадают в интервал значений показателей, допустимый для какого-то теоретического распределения, то этот закон принимается в качестве гипотезы и проверяется его соответствие экспериментальным данным по критериям согласия. В реальном случае из-за ошибок измерения оценки некоторых показателей