Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Downloads / pdf_in_archive (2) / 1_obrabotka.pdf

Скачиваний:

Добавлен:

02.04.2015

Размер:

1.05 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2812 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Рассмотрим несколько частных случаев:

1)зависимость имеет вид: y=a0. Составим систему (2.106):

]

[yx

]

€

[ y] =

mmin

0;mmax

j, k

∑yi

[ y]

]

N i=1

Sa€0 =

;S0

∑(yi −a€0 )

−1 i=1

y = a0 + a1 x

2) зависимость имеет вид:

Составляем систему (2.106):

a0 N + a1[x] =[ y]

mmin = 0;mmax =1 j = 0;1;k = 0;1 a

[x]

+ a

[x2

]=[ yx]

Из формулы (2.107) найдем:

€ = 0

N [x]

[ y]

[x]

]

;

[x] [x

]

;

[ yx]

]

;[x]

∑xi ;[x

∑xi ;[ y]

∑yi ;

i=1

[ yx] = ∑yI xi ;a€1 = 1

; 1 = N [ y]

i=1

[x]

[ yx]

Из (2.108) имеем для дисперсий:

2 = [x2 ]

2 =

−

€ +

€

2 +

;S0

∑[yi

)]

; Sy€( x)

Sa€1 .

Sa€0

S0 ;Sa€1

(a0

a1 xi

Sa€0

N −2 i=1

3)зависимость имеет вид: y=a1x. Составляем систему (2.106):

m =1;m

max

=1; j =1;k =1 a [x2

]=[ yx]

min

Nyi xi2

a€1 = [[xxy2 ]]= ∑i=1

∑xi

i=1

S02

Sa€1 =

;S0 =

∑(yi −a1 xi )

;Sy€( x) = x

Sa€1

N −

∑xi2

1 i=1

i=1

2.4. Методы оценки числа измерений

Для того, чтобы определить ошибку измерения, необходимы многократные измерения. Интуитивно ясно, что выполнять очень много измерений бессмысленно, так как точность результата всегда ограничена точностью метода. Кроме того из (2.15) следует, что СКО выборочного среднего S x убывает с увеличением числа измерений n не слишком

быстро, всего лишь как n , тогда как затраты на эксперимент растут

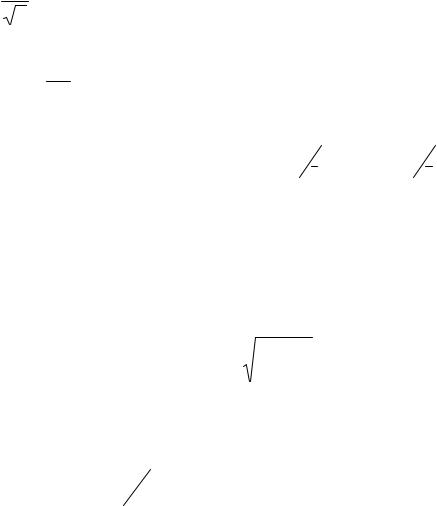
пропорционально n, т.е. могут быстро превысить потери от неточного знания результата измерения. Для получения объективных оценок необходимого числа измерений используется несколько методов.

2.4.1. Оценка числа измерений, необходимого для получения x с

требуемой точностью

а) Точечная оценка. Потребуем, чтобы СКО среднего не превышало некоторого допустимого значения:

S x ≤ S0 ,

где S0 – допустимое значение СКО среднего, ошибка, например, ошибка метода.

Тогда из (2.112) следует, что

S nn ≤ S0 ,

откуда и получаем оценку для n:

S 2 nx ≥ S n2

(2.112)

либо систематическая

(2.113)

где S n2 – выборочная дисперсия единичного измерения.
Вводя	относительные ошибки: εn = Sn x и ε0 = S0 x ,			можно (2.113)
представить в виде:
nx	≥	ε	2	(2.114)
		ε	n
			2
			0

б) Более сильная точечная оценка может быть получена из критерия

ничтожных	ошибок. Пусть ошибка измерения является суммой
нескольких	составляющих S Σ = ∑S(2k ) , в частности S Σ2 = S c2л. +S c2иcm. ,
	k

где Sc2л. – ошибка выборочного среднего, Sc2иcm. – например, методическая ошибка. Из критерия ничтожных ошибок следует, что частной ошибкой можно пренебречь, если S k ≤ 0,3S Σ , т. е. случайной ошибкой можно

пренебречь, если Sсист Sc‘. ≥ 3 , что дает:

	Sn	2	(2.115)
	Sn

n ≥11
	SСИСТ

в) Интервальная оценка:

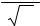
Для получения этой оценки потребуем, чтобы доверительный интервал для среднего не превышал некоторого допустимого значения:

	tα,k	S x ≤	0	(2.116)
где	0 – допустимое значение доверительного интервала.
	Из (2.116) следует, что
	nx	tα,k	S n	2
		≥		(2.117)

			0

где tα,k – значение определяемое из таблиц распределения Стьюдента при

уровне значимости α и числе степеней свободы k = n −1. Соотношение (2.117) является функциональным уравнением, так как n входит в обе части неравенства. Оно решается приближенно численным методом, подбором n с использованием таблиц распределения Стьюдента. Если n>30, то для оценки n можно использовать нормированное нормальное распределение и (2.117) преобразуется к виду:

	u		S	n	2
nx	≥	α		n	,	(2.118)
nx	≥				,	(2.118)
			0

где uα – определяется из таблицы н. н. р. и уже не зависит от n.

г) Точечная оценка числа измерений при косвенных измерениях. Пусть величина у связана с непосредственно измеряемыми

величинами известной функциональной зависимостью (см. раздел 2.2.5.)

yN	= f (xn(1) ,…, xn(k ) ).
	1	k

Тогда оценка для n может быть получена из условия равных влияний, а именно, потребуем, чтобы парциальные ошибки по всем аргументам были одинаковы (см. раздел 2.2.5.):

∂ f

(1) ≈…≈

( k ) =

(2.119)

∂ x n(1)

∂ x n(k )

x n1

x nk

где

N =

f (x n(11 ) ,…, x n(kk ) ).

Отсюда для числа измерений найдем:

S n

ni =

(2.120)

∂ f

∂ x (i)

(i)

x n

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2812 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>