расчётных значений. Именно этим и вызвано появление модификации (1.2.9) производственной функции Кобба-Дугласа.

Для того, чтобы решить эту проблему иногда меняют критерий МНК с (2.2.10) на следующий:

Конечно, в такому случае, фактически немного меняется вид исходной функции с (2.2.8) на:

но свойства модели от этого существенно не меняются, зато оценки коэффициентов a и b становятся несмещёнными, и у модели пропадает систематическое отклонение.

Метод подстановки заключается в следующем.

Предположим, что мы видим, что текущий ряд данных может быть лучше описан обратной функцией вида:

Если попытаться оценить параметры a и b функции (2.2.12) с использованием МНК «в лоб», то у нас возникнет множество проблем. Куда проще ввести новую переменную:

тогда функция может быть легко преобразована к линейному виду:

zt =a b xt .

Найти коэффициенты этой функции уже никаких сложностей не представляет.

Используя этот принцип можно очень многие функции привести к линейному виду. Например:

Множественная регрессия и эффект мультиколлинеарности

При построении многофакторных моделей иногда возникают ситуации, в которых факторы сильно коррелируют друг с другом. В таком случае говорят о наличии эффекта мультиколлинеарности, общая идея которого заключается в том, что оценки построенной модели становятся неустойчивыми. Например, после расчёта коэффициентов получается

модель: Y t =14,1 3,2 x1,t 6,3 x2,t , но после незначительного изменения исходных

данных (например, после округления или после добавления ещё дополнительного наблюдения в ряд данных) оценки модели меняются радикально:

Y t =1,1−7,1 x1, t 60,7 x2,t . Естественно, осуществлять адекватный прогноз в таких

32

условиях не представляется возможным, значит надо каким-то образом избавиться от эффекта мультиколлинеарности.

Всовременной эконометрике существует два направления по решению этой проблемы:

Впервом направлении выделяются два подхода:

•исключают из совокупности факторов одну или несколько линейно связанных факторных переменных, чтобы вновь полученные элементы корреляционной матрицы были меньше порогового значения 0,8.

Однако никаких формальных обоснований того, как выбрать исключаемый фактор и почему надо выбрать именно этот фактор, не существует. Соответственно этот подход нельзя назвать удовлетворительным.

•преобразуют факторы в новые переменные, уменьшая тем самым количество переменных (факторный анализ).

Врезультате такого подхода модель строится на основе некоторых фиктивных переменных, не обладающих никаким экономическим смыслом. Такое решение тоже нельзя назвать удовлетворительным.

Во втором направлении, совершенствовании математического аппарата оценивания коэффициентов модели используют методы регуляризации – раздел, называющийся «робастной статистикой», например, гребневой регрессии, стабилизированных оценок или «сжатых» оценок и т. п. Но это направление требует более обширных математических знаний и в результате использования этих методов также получаются переменные, не обладающие экономическим смыслом.

Для того, чтобы понять суть эффекта мультиколлинеарности и выработать лучшее решение этой проблемы, рассмотрим, в чём по сути заключается проблема.

момент времени t, a0, a1, a2 – коэффициенты модели, которые нам нужно найти. Критерий МНК для этой модели будет выглядеть следующим образом:

T

S=∑ Y t−a0−a1 x1, t−a2 x 2,t 2 min ,

t =1

или, если возвести в квадрат выражение в скобках:

T

S=∑ Y 2t −2 Y t a0 −2 Y t a1 x1,t −2 Y t a2 x2,t a20 2 a0 a1 x1,t 2 a0 a2 x2,t t =1

a12 x1,2 t 2 a1 x1,t a2 x2,t a22 x22,t

33

Рассчитывая частные производные S по коэффициентам, мы придём к следующей системе нормальных уравнений:

t=1

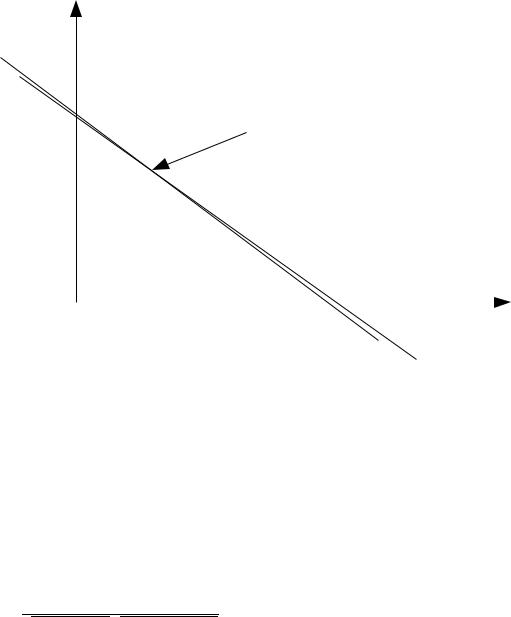
увидим, что эти значения буду очень близки друг к другу, а это фактически означает, что мы сталкиваемся как раз с ситуацией, в которой прямые на плоскости коэффициентов, описываемые уравнениями из системы нормальных уравнений, пересекаются под очень острым углом (обозначим его через γ). В результате, если мы меняем любое значение фактора, то также сдвигается точка пересечения между прямыми, то есть оценки модели становятся очень неустойчивыми. На рисунке 10 показан такой пример для случая с двумя коэффициентами и двумя уравнениями из системы (2.2.16), но картина будет идентичной и для всех остальных коэффициентов и уравнений из системы (2.2.16).

34

Рисунок 10: Эффект мультиколлинеарности на плоскости коэффициентов

Очевидно, что для решения проблемы мультиколлинеарности нужно просто каким-то образом развести эти прямые и увеличить угол γ между ними. Для этого вначале вспомним формулу для нахождения косинуса угла между гиперплоскостями.

Если гиперплоскости описываются уравнениями:

то косинус угла между ними находится по формуле:

Рассчитаем для начала косинус угла γ между первыми двумя уравнениями из системы

35

Для того, чтобы максимально развести прямые коэффициентов, угол γ должен стать прямым. Тогда оценки коэффициентов модели (2.2.14) станут устойчивыми и не будут так радикально меняться. А так как косинус прямого угла равен нулю, в формуле (2.2.18) нужно каким-то образом преобразовать числитель для того, чтобы вся дробь обратилась в ноль. А для этого достаточно осуществить операцию центрирования исходных данных, которая осуществляется по формулам:

{Y 't =Y t −Y

x '1,t= x1,t −x1

x '2,t =x2,t −x2 , (2.2.19)

...

x 'n , t= xn, t− xn

где Y , x1 , x2 ,..., xn - средние величины соответствующих факторов.

Если операцию центрирования осуществить перед началом расчётов, то мы в итоге придём к формуле (2.2.18) с центрированными переменными. А так как сумма

T

центрированных переменных равна нулю, то есть в нашей дроби (2.2.18) ∑ x '1,t =0 и

t =1

T

∑ x '2,t =0 , то и числитель всей дроби становится равным нулю. Таким образом угол γ

t =1

становится прямым и, как следствие, оценки модели (2.2.14) становятся устойчивыми. Такой подход позволяет избавить от эффекта мультиколлинеарности без уничтожения экономического смысла переменных и без применения сложных математических расчётов.

Мы показали, что для того, чтобы получить устойчивые оценки модели в условиях мультиколлинеарности достаточно осуществить предварительное центрирование исходных данных по формуле (2.2.19).

36