Тема 2. Методы прогнозирования обратимых процессов

2.1. Краткосрочное прогнозирование обратимых процессов

Средняя величина

При краткосрочном прогнозировании стационарных процессов последовательность данных рассматривается как реализация случайных величин с фиксированным распределением, которые в большинстве случаев считается нормальным с некоторым математическим ожиданием и дисперсией. Прогнозирование в такой ситуации сводится к вычислению математического ожидания, расчёту дисперсии и доверительных интервалов.

Лучшей оценкой математического ожидания для нормального распределения, как вы знаете, является средняя величина. Тогда прогноз на одно наблюдение вперёд будет равен:

дисперсия в свою очередь считается по формуле:

Зная эти 2 значения легко выполнить краткосрочный прогноз для стационарного процесса. Однако с учётом того, что обычно среднее значение рассчитывается по какой-то выборке наблюдений, а не по всей совокупности, истинное математическое ожидание находится в некотором интервале, который можно определить по формуле:

своему фактическому значению, следовательно основной путь повышения прогноза — увеличение числа наблюдений.

Рассмотрим пример. Студенты сдают экзамен и на выходе один из студентов собирает информацию для того, чтобы понять, что его может ждать. Выходит 5 человек со следующими оценками:

25

Похожий принцип с доверительными интервалами работает и в случае, когда мы сталкиваемся и с нестационарными процессами, а в качестве математического ожидания у нас выступает какая-то математическая функция. На семинарских занятиях мы будем рассчитывать доверительные интервалы по более простой, несколько некорректной с точки зрения эконометрии формуле:

Для наших целей этой формулы должно быть достаточно.

Обращаем ваше внимание на то, что на семинарских занятиях мы будем строить модели, в которых расчётное значение определяется не через среднее значение, а через какую-либо математическую функцию. В таком случае и СКО надо считать как отклонение фактических значений от нашей модели, а не от среднего арифметического.

Однако вернёмся к нашему случаю с нормальным распределением случайных величин. Если мы раскроем знак суммы в формуле (2.1.1), то получим:

мы имеем дело не с нормальным распределением случайных величин или хотим некоторым иным образом дать прогноз, то эти веса могут быть и разными. В таком случае можно использовать следующую формулу для расчёта прогнозного значения:

Y T 1=νT Y T νT −1 Y T −1 ... ν1 Y 1 ,

где νT - вес соответствующего значения YT на наблюдении T.

Авторегрессия

Достаточно часто на практике встречаются стационарные процессы, каждое значение Yt которых определяется предыдущими значениями Yt-1, Yt-2. То есть имеет место авторегрессия, формально описываемая следующей формулой:

26

Для того, чтобы определить, имеется ли в процессе такая зависимость и может ли он быть описан авторегрессионной моделью, осуществляется расчёт коэффициентов автокорреляции, для чего в формулу коэффициента корреляции подставляют попарно значения Y в момент t и те же, но сдвинутые на некоторый шаг τ.

Вспомним, как рассчитывается коэффициент корреляции между двумя переменными

— Xt и Yt:

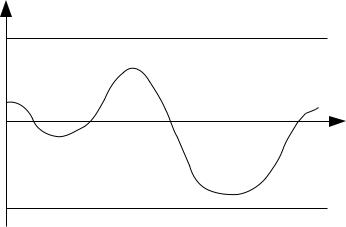
Если при некоем сдвиге τ коэффициент корреляции окажется по модулю не менее 0,8, то говорят о наличии линейной зависимости между значениями самого ряда и ряда, сдвинутого во времени (ряда с лагом). Обычно зависимость коэффициента корреляции от шага τ анализируют графически. Такой график называют коррелограммой (см. Рисунок 7).

τ

-0,91

-1

Рисунок 7: Пример коррелограммы

Если, например, оказалось, что коррелограмма имеет два по модулю наибольших значения (например, r5=0,87 и r7=−0,91 ), то исследователь имеет все основания для построения модели авторегрессии вида:

Y t =a5 Y t – 5−a7 Y t – 7 .

27