Для нахождения коэффициентов такой функции обычно пользуются методами математической статистики или численными методами.

2.2. Среднесрочное прогнозирование обратимых процессов

Парная регрессия и метод наименьших квадратов

Как мы уже говорили, в среднесрочном прогнозировании обратимых процессов обычно используют метод регрессии, который сводится фактически к изучению и построению той или иной зависимости между двумя или несколькими переменными. Примером таких моделей являются как раз ПФ, которые мы с вами рассмотрели чуть ранее.

Обычно для нахождения коэффициентов функции в эконометрике, как вы знаете, используют метод наименьших квадратов. Преимущество метода — в его простоте и в том, что оценки, найденные с использованием МНК являются несмещенными.

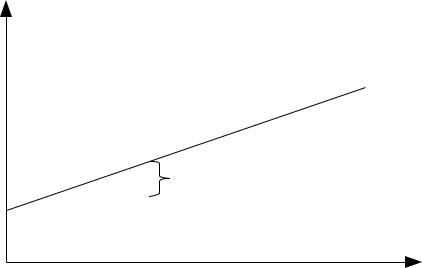
Вообще, давайте вспомним, какой смысл имеет МНК? Для этого обратимся к следующему рисунку (Рисунок 8).

Yt

Y t =a b xt

* * * * * *

xt

Рисунок 8: Графическая интерпретация МНК

В нашем распоряжении имеется некоторый ряд данных, и мы предполагаем (либо находим с помощью коэффициента корреляции), что этот ряд можно описать какой-то линейной функцией:

Строим эту функцию и видим, что она проходит около фактических значений с каким-

того, чтобы функция описала этот ряд данных наилучшим образом, надо подобрать такие коэффициенты a и b, чтобы все эти отклонения были минимальными. Однако, как видим, отклонения могут быть как положительными (когда фактическое значение лежит выше

28

расчётного), так и отрицательными (соответственно, ситуация наоборот). Если мы все эти отклонения просто сложим, то они сократятся и мы не получим реальную оценку ситуации — суммарное отклонение вполне может стать равным нулю. Для того, чтобы избежать этой ситуации и получить более адекватную оценку, все отклонения вначале возводят в квадрат, после чего суммируют и получают сумму квадратов отклонений:

различные значения коэффициентов a и b. Математически это означает требование:

Ну, а чтобы найти значения коэффициентов, при которых эта функция принимает минимальные значения, нужно взять производные S по a и по b и приравнять их нулю:

Решая полученные уравнения, мы вначале получаем следующую систему нормальных уравнений:

из которой можно легко вывести формулы для нахождения коэффициентов функции:

Врезультате расчётов по формулам (2.2.5) и (2.2.6) мы найдём такие коэффициенты a и b линейной функции (2.2.1), для которых выполняется условие (2.2.2), то есть сумма квадратов отклонений фактических значений от расчётных минимальна.

Вслучае, если мы строим тренд (зависимость какого-то показателя от времени), в

формулы (2.2.5) и (2.2.6) вместо xt надо просто подставить номер наблюдения t — в результате будет построен линейный тренд с коэффициентами a и b.

Стоит заметить, что когда мы строим регрессионные модели, переменными у нас фактически выступают коэффициенты, поэтому удобней регрессии представить несколько иначе. Так систему нормальных уравнений (2.2.4) можно представить ещё и через

29

уравнение в отрезках, разделив соответствующие левые и правые части уравнений на стоящие в правых частях суммы:

T∑T xt

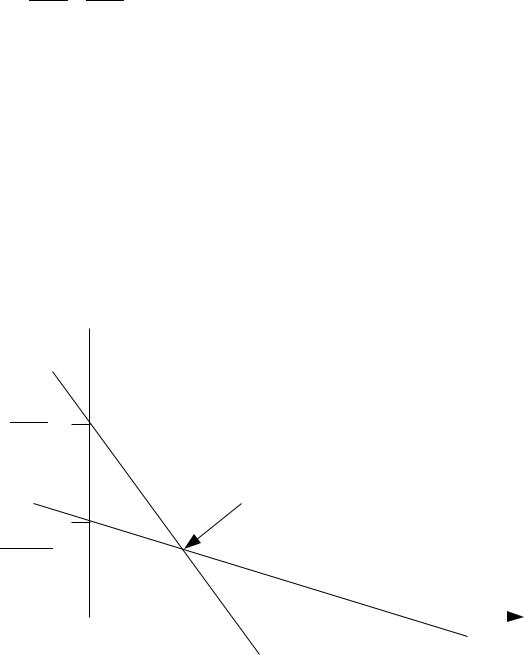
Такое представление позволяет построить на плоскости коэффициентов (в нашем случае по оси абсцисс будем откладывать a, по оси ординат — b) прямые, каждая из которых характеризует разное сочетание коэффициентов a и b, удовлетворяющее по отдельности каждому из уравнений (2.2.4). Точкой пересечения этих двух прямых будет пара коэффициентов a* и b*, являющаяся решением системы уравнений (2.2.4). Графически эта ситуация показана на рис. 9.

b

T

∑ Y t

t =1

T

∑ xt

t=1

(a*, b*)

T

∑ Y t xt

t =1

T

∑ x2t

t=1

Рисунок 9: Задача нахождения оптимума на плоскости коэффициентов модели

Такое представление позволяет несколько иначе взглянуть на задачу нахождения коэффициентов модели с помощью метода наименьших квадратов: она заключается в том,

30

что отдельно для каждого из уравнений системы (2.2.4) существует бесконечное множество решений, но в самой системе в общем случае оно только одно. Впрочем, нельзя отрицать, что теоретически возможна ситуация, в которой прямые (1) и (2) на рис. 9 не будут пересекаться, а, например, сольются. Тогда в результате решения системы (2.2.4) мы не получим точечной оценки — то есть найти истинное значение коэффициентов модели будет невозможно.

Метод наименьших квадратов прекрасно работает в случае с линейными функциями, но очевидно, что не всегда линейная функция описывает ряд лучше всех остальных. В таких случаях появляется потребность найти коэффициенты других функций. Например, степенных, экспоненциальных, тригонометрических, обратных и др. функции. Для оценки таких моделей также можно применить МНК. В таких случаях имеющуюся модель нужно вначале привести к виду линейной, используя один из двух методов:

1.Метод линеаризации,

2.Метод подстановки.

Метод линеаризации обычно применяется в случаях с экспоненциальными или степенными функциями — в тех случаях, когда его невозможно применить напрямую, и заключается в том, что в функции логарифмируется и левая, и правая части, после чего находятся коэффициенты, при которых достигается минимум суммы квадратов отклонений линеаризованных функций.

Рассмотрим пример со степенной функцией:

Линеаризуем функцию (2.2.8) используя натуральные логарифмы. Получим:

После этого МНК без проблем применяется уже к функции (2.2.9), а не (2.2.8). В итоге минимизируется следующая сумма квадратов отклонений:

Если теперь найти частные производные (2.2.10) по коэффициентам a и b, аналогично (2.2.3), то мы найдём коэффициенты, для которых сумма отклонений (2.2.10) минимальна. Однако стоит обратить внимание на то, что мы минимизируем эту самую линеаризованную функцию, а не изначальную. А в связи с тем, что всегда при расчёте коэффициентов есть небольшая ошибка, то после расчёта, по возвращении к нормальной, не линеаризованной форме, она возрастает экспоненциально. Причём, экспонирование приводит к тому, что ошибка становится положительной, и распределённой со смещением. В результате этого у модели появляется систематическое отклонение от

31