
- •Литература
- •План курса
- •Тема 1. Математические методы в экономике
- •1.1. Введение
- •1.2. Модели математической экономики. Производственные функции
- •1.3. Эконометрические модели
- •Тема 2. Методы прогнозирования обратимых процессов
- •2.1. Краткосрочное прогнозирование обратимых процессов
- •Средняя величина
- •Авторегрессия
- •2.2. Среднесрочное прогнозирование обратимых процессов
- •Парная регрессия и метод наименьших квадратов
- •Множественная регрессия и эффект мультиколлинеарности
- •Тема 3. Методы прогнозирования необратимых процессов
- •3.1. Краткосрочное прогнозирование. Модель Брауна
- •3.2. Среднесрочное прогнозирование
- •МНК с дисконтированием
- •Модификации метода Брауна
- •Метод стохастической аппроксимации (МСА)
- •Тема 4. Финансовая математика
- •4.1. Основные термины и принципы финансовой математики
- •4.2. Модели расчетов с простыми и сложными ставками
- •Простые проценты
- •Плавающие ставки по простым процентам
- •Учёт нецелых периодов наращения в банковском секторе
- •Простые учётные ставки
- •Сложные проценты
- •Плавающие ставки по сложным процентам
- •Связь между простыми и сложными процентами
- •Смешанная формула расчёта процентов
- •Сложные учётные ставки
- •Связь между простыми и сложными учётными ставками
- •Уравновешенные и относительные ставки
- •Непрерывные проценты
- •Учёт инфляции
- •4.3. Операции с платежами
- •Финансовая эквивалентность
- •Консолидация платежей по формуле простых процентов
- •Замена платежей по формуле простых процентов
- •Консолидация и замена платежей по формуле сложных процентов
- •Консолидация платежей по формулам банковского учёта
- •Разъединение платежей по формулам простых и сложных процентов
- •4.4. Потоки платежей
- •Общие понятия и приведённая стоимость потока платежей
- •Оценка эффективности инвестиционного проекта
- •Приведённая стоимость потока инвестиций (расходов) K
- •Приведённая стоимость потока доходов D
- •Чистая приведённая стоимость (NPV)
- •Внутренняя норма доходности проекта (IRR)
- •Индекс доходности проекта (PI)
- •Срок окупаемости проекта (DPP)
- •Модифицированная внутренняя норма доходности MIRR (Modified IRR)
- •Приведённая стоимость финансовой ренты
- •4.5 Конверсия валют
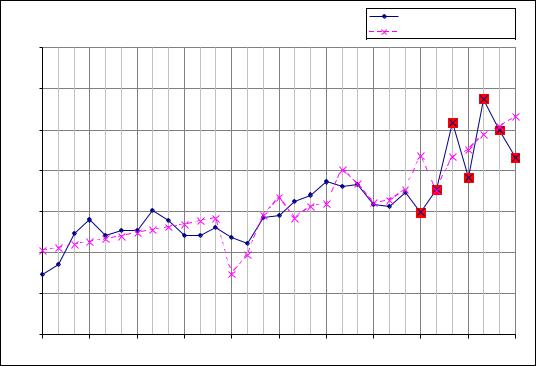
Некоторые исследователи утверждают, что модель Тейла-Вейджа для некоторых рядов |
|||||
данных (в частности, для рядов, в которых не происходит резких изменений) даёт |
|||||
результаты лучше, чем модель Холта-Уинтерса. Однако эта информация не очень хорошо |
|||||
проверена и по результатам многочисленных построений модели на практике |
|
||||
складывается ощущение о том, что модель по своим свойствам идентична модели Холта- |
|||||
Уинтерса и практически всегда даёт такой же прогноз. |
|
|
|
|
|
Мировые продажи гибридных автомобилей |
|
|
Факт |
|
|
Модель Холта-Уинтерса |
|
|
Модель Холта-Уинтерса |
||
70,00 |
|
|
|
|
|
60,00 |
|
|
|
|
|
50,00 |
|
|
|
|
|
40,00 |
|
|
|
|
|
30,00 |
|
|
|
|
|
20,00 |
|
|
|
|
|
10,00 |
|
|
|
|
|
0,00 |
|
|
|
|
|
янв.05 апр.05 июл.05 окт.05 янв.06 апр.06 |
июл.06 |
окт.06 |
янв.07 |
апр.07 |
июл.07 |
Рисунок 20: Прогнозирование продаж гибридных автомобилей с помощью |
|||||
модели Холта-Уинтерса |
|
|
|
|
|
Стоит заметить, что в случаях, когда мы имеем дело с системами с большим периодом инерционности, предположения, положенные в основу модификаций модели Брауна, действительно могут выполняться, и тогда прогноз, получаемый по этим моделям оказывается более точным, нежели прогноз по любой другой модели.
Метод стохастической аппроксимации (МСА)
Очевидно, что в необратимых процессах имеются как незначительные отклонения от тех или иных тенденций, вызванные влиянием различным неучтённых факторов или просто ошибками, так и систематические отклонения, вызванные изменением самой структуры процесса. Совершенно естественно, что если модель будет относиться к ним одинаково, то прогнозные свойства её будут не идеальными. Именно это мы видели на примере различных модификаций метода Брауна: коэффициенты корректировались на каждом шаге под фактические данные, без учёта характера этих данных. Метод стохастической аппроксимации позволяет разрешить эту вопиющую несправедливость.
Рассмотрим, как можно применять метод на примере линейной функции:
|
(3.2.15) |
Y t=a bxt . |
53
Если перед исследователем стоит задача использования метода стохастической аппроксимации для нелинейных функций, то их надо вначале просто привести к линейному виду (путём линеаризации или подстановки), после чего уже применять метод. Предположим, что мы уже нашли коэффициенты модели, например, с помощью того же МНК либо по всему ряду данных, либо по какому-нибудь первому участку. В случае с МСА (в отличие от метода Брауна и его модификаций) особой разницы, каким образом были найдены коэффициенты нет.
От полученной линейной функции имеются некоторые отклонения, часть из которых характеризует случайную (или неопределённую) составляющую, другая часть — систематические отклонения, вызванные структурными изменениями. Как их отделить друг от друга? В МСА заложен следующий механизм.
Исследователь задаёт величину η, характеризующую границы, в которых должны лежать отклонения (своеобразный доверительный интервал):
|
ˆ |
− η , |
(3.2.16) |
нижняя граница характеризуется величиной Yt |
|||
ˆ |
+ η . |
|
(3.2.17) |
верхняя — Yt |
|
||
Далее на каждом шаге оценивается, попало ли фактическое значение в этот интервал или нет. Если оно оказывается между (3.2.16) и (3.2.17), то модель не имеет смысл адаптировать. Если же она выходит за эти пределы, значит модель нужно каким-то образом адаптировать.
Математически это можно формализовать следующим образом. На каждом шаге рассчитывается величина отклонения фактических значений от расчётных (ошибка):
|
(3.2.18) |
εt=Y t −Y t . |
На каждом же шаге полученная величина сравнивается с заданной исследователем η. Если оказывается, что |εt | ≤ η , то пересчитывать модель нет смысла. Если же |εt | > η , то мы модель должна адаптироваться.
Однако для начала надо понять, как рассчитать значение εt . Для этого, как мы уже заметили, нужно отнять от фактического значения Y расчётное значение. В случае с линейной моделью (3.2.15), имеем:
ˆ |
(3.2.19) |
εt = Yt − Yt = Yt − bxt − a . |
Выразим теперь значения коэффициентов a и b через остальные параметры модели:
|
|
|
(3.2.20) |
a=Y t −b xt , |
|||
|
|
|
|
b= |
Y t −a |
. |
(3.2.21) |
xt |
|||
В случае, если в формулу (3.2.20) подставить фактические значения Y, то будем иметь следующую величину отклонения:
Yt − bxt − a = εt . |
(3.2.22) |
54

Если в формулу (3.2.21) подставить фактические значения, то величина отклонения
будет следующей: |
|
|
|
|
|
|||
|
Y t−a |
−b= |
Y t−a−bxt |
= |
εt |
. |
(3.2.23) |
|
|
|
|
|
|||||
|
xt |
xt |
xt |
|
||||
То коэффициент a будет в себе содержать ошибку εt , а коэффициент b — ошибку
εt |
. Значит для того, чтобы адаптировать модель, нужно модифицировать её |
xt |
коэффициенты на соответствующие величины ошибок. Это можно сделать следующим образом:
a |
|
=a |
+γ |
ε |
|
, b |
|
=b |
+γ |
|
εt |
, |
(3.2.24) |
|
|
|
|
|
|||||||||
|
t+1 |
t |
t |
|
t |
|
t+1 |
t |
|
t xt |
|
||
где γt - параметр демпфирования колебаний.
В зависимости от того, каким образом мы задаём γt , модель у нас либо быстро, либо
медленно адаптируется к новым условиям. То есть коэффициент демпфирования колебаний характеризует степень адаптации коэффициентов модели.
Существуют разные варианты задания γt . Из самых простых можно выделить два:
1.γt можно задать постоянным для всего ряда (по аналогии с постоянной
сглаживания в модели Брауна): γt = Тогда модель всегда будет меняться на какую-то фиксированную величину;
|
1 εt − |
|
||
2. γt можно рассчитать по формуле: γt = |
|
|
|
, где m – количество |
m |
εt |
|||
коэффициентов модели. В таком случае модель каждый раз будет подтягиваться своей крайней границей к фактическому значению;
3.γt можно рассчитать по смешанной формуле, учитывающей оба эти варианта:
γt = 1 εt − . Тогда модель будет подтягивать не границы к фактическим m εt
значениям, а какие-то значения внутри интервала (например, сами точечные значения). Правда, в таком случае она становится более чувствительной к случайным отклонениям.
Модель стохастической аппроксимации очень тяжело выразить системой уравнений в общем виде, но в частном случае (с линейной функцией с одним фактором и вторым
принципом задания γt ) она может быть выражена следующим образом:
|
, |
Y t 1=at bt xt |
εt=Y t −Y t
55

a =a |
|
и {btt=att−−11 , если εt |
, |
{at =at −1 γt εt
bt =at −1 γxt εt t , если εt .
γt = 1 εt − m εt
Преимущества модели Стохастической аппроксимации:
1.Модель позволяет описать любую тенденцию — для этого достаточно выбрать первоначальную функцию вместо (3.2.15) и вывести формулы для пересчёта коэффициентов модели;
2.Модель позволяет описывать многофакторные зависимости (а не только зависимость от времени, как модификации метода Брауна);
3.Модель даёт хорошие прогнозы в случае со среднесрочным прогнозированием, так как «отсеивает» шумы и адаптируется только к существенным изменениям тенденций.
Недостатки:
1. Нет никакого алгоритма задания величины — его значение выбирается полностью на основе экспертных оценок;
2.Модель громоздка. Причём, чем больше в ней факторов, тем больше она требует расчётов;
3.Нет никакого обоснования того, каким образом должны рассчитываться первоначальные значения коэффициентов;
Рассмотрим на нашем примере, как будет выглядеть модель, построенная по МСА (рисунок 21). =9,84 , γt задан по смешанной формуле.
56

|
|
|
|
|
|
|
|
|
Факт |
|
Мировые продажи гибридных автомобилей |
|
|
|
МСА |
||||||
|
|
|
^Y-η |
|||||||
|
Метод стохастической аппроксимации |
|
|
|
|
|||||
|
|
|
|
|
^Y+η |
|||||
|
|
|
|
|
|
|
|
|
||
70,00 |
|
|
|
|
|
|
|
|
|
|
60,00 |
|
|
|
|
|
|
|
|
|
|
50,00 |
|
|
|
|
|
|
|
|
|
|
40,00 |
|
|
|
|
|
|
|
|
|
|
30,00 |
|
|
|
|
|
|
|
|
|
|
20,00 |
|
|
|
|
|
|
|
|
|
|
10,00 |
|
|
|
|
|
|
|
|
|
|
0,00 |
|
|
|
|
|
|
|
|
|
|
янв.05 |
апр.05 |
июл.05 |
окт.05 |
янв.06 |
апр.06 |
июл.06 |
окт.06 |
янв.07 |
апр.07 |
июл.07 |
Рисунок 21: Прогнозирование продаж гибридных автомобилей с помощью |
||||||||||
метода стохастической аппроксимации |
|
|
|
|
|
|||||
По рисунку 21 видно, как модель аппроксимирует ряд данных: важно не то, чтобы расчётные значения были как можно ближе к фактическим, а то, чтобы фактические попадали в заданный исследователем интервал. Из-за этого у модели в нескольких местах появляется систематическое завышение или занижение, однако, это и неважно в случае, если нас интересует интервальный прогноз. Вообще же в нашем примере точность прогноза по модели стохастической аппроксимации оказалась сопоставимой с точностью прогноза по модели Холта-Уинтерса.
57
