Во втором случае сумма получится иной:

S2=100 1 0,15 180365 ≈100 1 0,0739 =107,39

Разность в итоговых суммах составит S1−S2 =0,11 . В случае, если речь идёт о небольшом вкладе, эта разница не является существенной, ей можно пренебречь. Однако, если речь идёт о вкладах в размере 100 млн. рублей, то разница в 110 тыс. рублей уже становится ощутимой. Более того, этот разрыв увеличивается со сроком, на который сделан вклад.

Однако самые сложные вычисления в банковском секторе связаны с расчётами точных процентов по вкладам на стыке високосного и не високосного годов, ведь в таком случае не понятно, что брать за базу: 365 или 366 дней.

Так, например, в случае, когда t0 = 01.09.2007, а t1 = 01.03.2008, корректная формула

Кроме того, в банковских расчётах важную роль также играют условия вклада. Например, в условиях может быть оговорено, что в расчёте не должен участвовать первый либо последний день. В таком случае в формуле (4.2.8) в числителе к количеству дней может быть прибавлен или вычтен 1 день.

В MS Excel есть функция для расчёта этой доли год. В русской версии она называется «=Долягода(t0, t1, a)». В английской версии - «=yearfrac(t0, t1, a)». Здесь t0 — дата начала вклада, t1 — дата окончания вклада, a — параметр, определяющий временную базу. Подробней о функции можно почитать в «Справке» к MS Excel. Функция, к сожалению, не учитывает разницу во временной базе при переходе от високосного года к не високосного, из-за чего итоговые значения точных процентов, рассчитанных по ней, оказываются некорректными.

Простые учётные ставки

Выше были приведены формулы, которые позволяют по начальной величине вклада P определить конечную сумму S. В финансовой практике часто возникает и обратная задача: по заданной конечной сумме S определить необходимую начальную величину Р. Такая задача возникает, например, при применении учетной ставки, когда проценты с суммы S удерживаются при выдаче кредита. Такая же задача возникает при получении платежных обязательств (например, векселей), расчет по которым будет производиться в будущем.

Ранее мы уже упоминали о том, что такое дисконт D и операция дисконтирования. Стоит заметить, что дисконтирование используют не только в задачах, связанных с проведением той или иной конкретной финансовой операции (выдаче векселя, ссуды и т.п.). Оно имеет гораздо более широкий круг применения. Так дисконтирование фактически позволяет дать денежную оценку времени.

В зависимости от целей дисконтирования используют две формулы расчета. Одна связана с математическим дисконтированием. Другая — с банковским учетом. При расчетах по математическому дисконтированию (при простой процентной ставке) исходят

66

из формулы (4.2.3). Эта формула выражает конечную сумму S через начальную величину Р, а значит из неё можно сразу получить выражение, определяющее начальную величину Р через конечную сумму S:

называется формулой математического дисконтирования.

При расчётах по схеме банковского учёта используют другую формулу, выражающую начальную величину P через конечную сумму S:

Стоит заметить, что величина t обычно представляет собой промежуток времени от момента вклада денег до момента их получения назад. Так, например, при расчёте реальной стоимости векселей t характеризует промежуток времени между моментом приобретения векселя и моментом его погашения. Чем ближе этот промежуток к нулю, тем ближе реальная стоимость векселя к его номинальной стоимости.

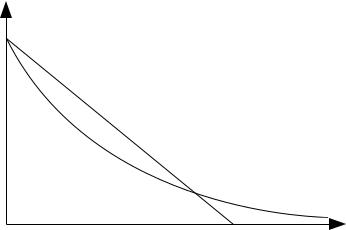
Математическое дисконтирование точным и корректным образом связывает исходную и конечную величины, P и S. Зависимость дисконтного множителя от времени t при математическом дисконтировании графически представляется в виде ветви гиперболы, которая с увеличением t стремится к 0 (рисунок 24). Оно активно используется в теоретическом финансовом анализе, при оценке проектов, однако на практике, в коммерческих операциях, при покупке векселей и других платежных обязательств, используют схему банковского учета. Зависимость величины P в формуле (4.2.10) от времени имеет вид прямой линии, тангенс угла наклона которой равен Sd, то есть определяется учетной ставкой, взятой с противоположным знаком: чем больше ставка, тем больше угол наклона, тем быстрее будет погашено обязательство (рисунок 24).

P

S

(4.2.10)

(4.2.9)

Рисунок 24: Соотношение между математическим и банковским дисконтированием

67

Стоит заметить, что при расчёте реальной стоимости векселя по формуле (4.2.10) теоретически можно прийти к моменту времени, в котором его стоимость равна нулю, что в общем-то не имеет экономического смысла. Но на практике с такой ситуацией столкнуться невозможно, так как векселя имеют такие сроки погашения, для которых реальная сумма не может быть близка к нулю.

Рассмотрим пример. Предположим, что нас интересует, какую сумму денег нужно вложить для того, чтобы через год получить 120 тыс. руб. при i = 20%. В таком случае получим по формулам (4.2.9) и (4.2.10):

Фактически первая формула характеризует то, какую сумму мы должны положить на счёт, чтобы получить 120 тыс. руб., а вторая — какой вексель нам нужно купить: с номинальной стоимостью в 120 тыс. руб., реальною стоимостью в 96 тыс. руб., со ставкой 20%.

Приведенные выше формулы позволяют определить срок вклада, величину процентной или учетной ставки через остальные характеристики условий вклада. Эти же формулы могут быть использованы и для других финансовых операций, в том числе и при заключении договоров о ссудах, кредитах.

Для определения продолжительности кредита следует соответствующим образом преобразовать исходные формулы. Из формулы (4.2.3), определяющей характеристики кредита через процентную ставку i, получаем:

Фактически перед нами формула, числитель которой характеризует сумму процентов за весь срок сделки, а знаменатель — сумму процентов за один период. Их отношение как раз и даёт нам срок сделки.

Из формулы (4.2.10), определяющей характеристики кредита через учетную ставку d, получаем:

Вформуле (4.2.12) числитель аналогично формуле (4.2.11) характеризует сумму дисконта за весь срок сделки, а знаменатель — дисконт за один период. Их отношение также даёт срок действия сделки.

Вобеих расчетных схемах, и по процентной, и по учетной ставке, время кредита прямо пропорционально приращению средств (проценту или дисконту) и обратно пропорционально величине ставки (процентной или учетной).

Аналогичным образом можно выразить величину ставки через остальные характеристики кредита. Для процентной ставки i получим:

68

В формуле (4.2.13) в числителе представлена сумма процентов, наращенных за весь срок по некоторой ставке, а в знаменателе — фактически сумма процентов, которая могла бы быть наращена за этот же срок, если бы ставка i была равна 100%. Их отношение как раз даёт нам некоторую долю, соответствующую величине процентной ставки.

А для учётной ставки d получим:

Толкование этой формулы может быть дано идентично толкованию формулы (4.2.13): в числителе представлен дисконт за весь срок по некоторой учётной ставке, а в знаменателе — фактически дисконт, который мог бы быть получен за этот же срок, если бы ставка d была равна 100%. Их отношение даёт нам долю, соответствующую величине учётной ставки ставки.

Пример.

Ссуда в размере 100 000 рублей выдана на условиях начисления простых процентов по годовой ставке 25%. Через какое время накопленная величина долга станет равна 150 000 рублей?

Решение.

По формуле (4.2.11) имеем:

t=S −P = 150000−100000 =2 iP 0,25 100000 .

Поскольку по условию задачи процентная ставка годовая, то и рассчитанное по формуле время выражено в годах. Таким образом ответ: через 2 года.

Пример.

По договору предусмотрено погашение кредита через 4 месяца в сумме 120 000 рублей. Первоначальная величина кредита составляет 100 000 рублей. Требуется определить величину годовой процентной ставки и величину годовой учетной ставки.

Решение.

Для начала надо перевести месячные периоды в годовые. 4 месяца составляют 1/3 года. По формулам (4.2.13) и (4.2.14) определяем:

i= S−P =120000−100000 =0,6=60% , tP 1/3 100000

d =S −P =120000−100000=0,5=50% . tS 1/3 120000

69