
Doc / КОЩАНОВА Г.Р.АЛГЕБРА ЖӘНЕ ГЕОМЕТРИЯ
.pdfШешуі. Сипаттауыш теңдеудің
|
|
|
|
|
|
|
2 |
|
|
0 |
|
|
|
|
2 1 2 0 |
|
||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
det A E |
|
0 |
|
2 |
|
|
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
түбірлері |
1 2, 2 1, 3 |
1 |
болады. |
Демек, |
матрица диоганаль түрге келтіріледі. |
|||||||||||||||||||||||
Сәйкестелген меншікті векторларын табамыз. |
|
1 |
2 |
болғанда |
A E X 0 жүйе |
|||||||||||||||||||||||
келесі түрге келтіріледі: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
0 x1 |
|
|
0 |
|
|
|||||||||||||
|
|
A E X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
0 |
|
|
0 |
|
0 |
|
|
x2 |
|
|
0 |
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
3 x3 |
|
|
|
|
|
||||||||||||||||
немесе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 2x2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
3x |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2x 2x |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Шешімдердің фундаментальды жүйесі тек қана бір |
|
E1 2, 1, 2 T |
вектордан тұрады. |
|||||||||||||||||||||||||
Осы сияқты 2 1 болғанда |
A E X 0 жүйе келесі түрге келтіріледі: |
|||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
2 |
|
0 x1 |
|
|
0 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
A E X |
|
0 |
|
1 |
|
0 |
|
|
|
x2 |
|
|
0 |
|
|
|
||||||||||
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
0 |
|
|
|
||||||||||
|
|
|
|
|
|
x3 |
|
|
|
|
||||||||||||||||||
немесе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2x 2x |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
түрге келеді. Бұл жүйеден екінші меншікті |
векторды табамыз: E2 1, 0, 1 T . Соңында |
|||||||||||||||||||||||||||
сияқты 3 |
1 болғанда |
жүйе келесі түрге келтіріледі: |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
2 |
|
2 0 x1 |
|
0 |
|
|
||||||||||||||||
|
|
A E X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0 |
|
3 0 |
|
x2 |
|
0 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
2 |
0 |
|
|
|
|
|
0 |
|
|
|
||||||||||
|
|
|
|
|
|
|
x3 |
|
|
|
|
|||||||||||||||||
немесе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 x2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
3x2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
жүйеден үшінші меншікті векторды табамыз: E3 0, |
0, 1 T . |
|
|
|
|
|
|
|
||||||||||||||||||||
Табылған |
E1 2, 1, 2 T , E2 1, |
0, 1 T , |
E3 0, |
0, 1 T |
векторлар ізделінді базисті құрайды, |
|||||||||||||||||||||||
бұл базистегі сызық түрлендірудің А матрицасы келесі диоганальды түрге келеді:
71
2 |
0 |
0 |
||
|
|
|
|
|
A |
0 |
1 |
0 |
|
|
0 |
0 |
1 |
|
|
|
|
|
|
4.8. Тҥйіндес тҥрлендіру
|
|
|
|
|
|
|
Бізге Евклид R кеңістігінде сызықты |
түрлендіруі берілсін: R R . |
|
|
|
||
4.14-анықтама. Евклид кеңістігіндегі |
* |
сызықты түрлендіру |
|
* |
|
, егер кез- |
R R |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
келген |
x, y R элементтер үшін |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x , |
y x, * y , |
x, |
y R |
|
|
|
(4.31) |
|||
теңдігі орындалса, түрлендіруінің түйіндес түрлендіруі деп аталады. |
|
|||||||||||||
4.8-теорема. Евклид R |
кеңістігінде кез келген сызықты түрлендіруінің тек |
|||||||||||||
бір ғана |
* сызықты түйіндес түрлендіруі бар. |
|
|
|
|
|
|
|||||||
Дәлелдеуі. |
R |
кеңістігінде берілген y пен |
x |
элменттерін алып, мына теңдікті |
||||||||||
қарастырайық: |
|
|
|
|
f x x , y , |
|
|
|
|
|
|
|||
|
|
|
|
|
|
x R, |
y R , |
|
(4.32) |
|||||
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
мұндағы |
f : R V , ал V - нақты сандар кеңістігі. |
|
|
|
|
|
|
|||||||
Қарастырмақшы болған f x |
функциясының сызықты болатынын дәлелдейік. |
|||||||||||||
Ол үшін |
түрлендіруінің сызықты болатынын ескерсек жеткілікті: |
|
||||||||||||
|
f x x x z , y x z , y x , y z , y |
|
||||||||||||
|
f x f z , |
x R, |
y R, z R. |
|
|
|
|
|
|
|||||
Енді f x функциясының сызықты және тӛменгі теоремадан теңдігін аламыз: |
|
|||||||||||||
Егер l1 , l2 , ..., ln |
евклид кеңістігінің ортонормалданған базисі |
болса, онда R |
||||||||||||
кеңістігінде анықталган сызықты |
f x функцияға және |
оның |
базисінде |
тәуелді |
||||||||||
векторы |
a R табылып, |
ол |
f x функция |
x |
пен |
a |
векторларының |
скаляр |
||||||
кӛбейтіндісіне тең болады: |
|
|
f x x, a |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
мұндағы |
a a1 , a2 , |
..., an , ai |
f li , i |
|
. |
|
|
|
|
|
|
|||
1, n |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
f x x, a , |
x R, |
a R |
|
(4.33) |
|||
мұндағы x - кез келген элемент, |
a - берілген элемент. Олай болса, |
(4.22) мен (4.33) |
||||||||||||
формулаларын салыстырып |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x , y x, a , x R |
|
|
(4.34) |
|||||
72
теңдігін |
аламыз. Демек, (4.34) теңдік y a |
орындалатын |
түрлендіруінің |
||||
сызықты болатынын айқындайды, яғни |
|
|
|
|
|||
|
|
|
x , y x, y |
(4.35) |
|||
түрлендіруінің сызықты болатынын дәлелдейік. Шынында да, (4.35) теңдіктен |
|||||||
|
|
x, y z x , y z x , |
y x , z |
|
|||
|
|
x, y x, z x, a y z , |
y R, z R, x R. |
||||
|
* теңдігі орындалатынын кӛрсетейік. (4.35) |
формуладан x , y x, y |
|||||
және (4.31) теңдіктен x , y x, * y 0. Онда |
|
|
|
||||
|
|
x, * y x, y 0 |
және x, * |
y 0 |
|
||
Осыдан барлық y R үшін |
* y 0 |
теңдігі орындалады, яғни * . |
|||||
|
Анықталған * түрлендіруі тек біреу ғана болатынын дәлелдейік. |
||||||
Ол үшін |
мұндай түрлендіруді екеу деп қарастырайық, яғни 1* . |
Бұл жағдайда |
|||||
(4.35) |
формуладан: |
|
|
|
|
|
|
|
|
x , y x, * y және x , |
y x, 1* y |
|
|||
теңдіктері орындалады. Онда |
|
|
|
|
|
||
|
|
x, * y x, 1* y , x, * 1* y 0 |
|
||||
Осыдан * * y 0, яғни |
* *. Теорема дәлелденді. |
|
|||||
|
|
1 |
1 |
|
|
|
|
Енді |
|
түйіндес түрлендіруінің қасиеттерімен танысайық. |
|
||||
1.Бірлік түрлендіруінің түйіндесі ӛзіне тең, яғни .
2.Нӛлдік түрлендіруінің түйіндесі ӛзіне тең, яғни 0 0 .
3.Сызықты түрлендірулердің қосындысының түйіндесі олардың түйіндестерінің қосындысына тең, яғни
1 |
|
|
|
|
2 |
1 |
2 . |
||
4. . |
|
|
|
|
5. Түйіндес түрлендірулердің түйіндесі сызықты түрлендірудің ӛзіне тең , яғни
.
6. Сызықты түрлендірулердің кӛбейтіндісінің түйіндесі олардың түйіндестерінің кӛбейтінділеріне тең, яғни
1 |
|
|
|
|
2 |
1 |
2 . |
Дәлелдеуі. Жоғарыдағы қасиеттердің дәлелдемесі бірдей болғандықтан, 5-қасиеттің дәлелдемесін кӛрсетейік. Сонымен,
73
|
x , y x, * y |
* y , x y, |
x x , y |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Осыдан x |
x , |
яғни |
. |
|
|||
|
|
|
|||||
4.9. Симметриялы тҥрлендіру
4.15-анықтама. Егер евклид R кіңістігіндегі сызықты түрлендіру ӛзінің түйіндес
түрлендіруіне тең болса: онда ол симметриялы деп аталады. |
|
|
4.9-теорема. Евклид R кеңістігіндегі сызықты түрлендіру |
симметриялы болу |
|
үшін, барлық x, y R элементтері үшін |
|
|
x , y x, y , |
x, y R |
(4.36) |
теңдігі орындалуы қажетті әрі жеткілікті.
Қажеттілігі. Берілген түрлендіруі симметриялы болсын деп ұйғарып, (4.36) теңдікті дәлелдейік. Онда
x , y x, y x, y .
Жеткіліктігі. (4.36) теңдігі орындалсын деп ұйғарып, теңдігін дәлелдейік. Онда (4.36) теңдіктен:
x, y x , y x, y .
Осыдан |
|
болды. Теорема дәлелденді. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||
Енді симметриялы түрлендірудің негізгі қасиеттерімен танысайық. |
||||||||||||||||
1. Егер |
түрлендіруі симметриалы |
|
болса, онда |
|
мен |
|
түрлендірулері |
|||||||||
|
|
|||||||||||||||
аустырымды болады, яғни |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Шынында да, берілген түрлендіруі симметриялы . |
|
|
|
|||||||||||||
Сондықтан, |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. Егер |
|
мен |
|
түрлендірулері симметриалы болса, |
онда |
|
, және |
|||||||||
1 түрлендірулері |
|
|
|
симметриялы |
|
|
болады, |
яғни |
||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
, 1 1. |
|
|
|
|
|
|
||||||
Шынында да, |
|
|
|
|
|
|
|
|
1 |
1. |
||||||
, , 1 |
|
|||||||||||||||
3. Егер |
|
мен түрлендірулері симметриялы болса, онда |
түрлендіруі |
|||||||||||||
симметриялы болу үшін, олар ауыстырымды болу қажетті әрі жеткілікті. |
||||||||||||||||
Қажеттілігі. |
|
|
симметриялы болсын: |
* деп ұйғарып, |
||||||||||||
теңдігін дәлелдейік. Онда
74
* * *
Жеткіліктігі. |
|
ауыстырымды |
болсын |
деп |
ұйғарып, |
* теңдігін дәлелдейік. Онда
* * *
4.10. Ортогонал тҥрлендіру
4.16-анықтама. Евклид R кеңістігінің сызықты түрлендіруі ортогонал деп аталады, егер барлық x, y R элементтері үшін
x , y x, y (4.37)
теңдігі орындалса.
4.10-теорема. Евклид R кеңістігінің сызықты түрлендіруі ортогонал болу үшін,
оның түйіндес түрлендіруі кері түрлендіруге тең болуы |
|
* 1 |
(4.38) |
қажетті әрі жеткілікті.
Қажеттілігі. Евклид R кеңістігінің сызықты түрлендіруі ортогонал болсын, яғни
(4.37) теңдік орындалады. (4.38) теңдікті дәлелдейік. Онда (4.37) теңдіктен:
х, y x , y x, y
Осыдан * E . Онда * 1 болады. |
|
Жеткіліктігі. Евклид R кеңістігінің сызықты түрлендіруі үшін |
(4.38) теңдігі |
орындалсын. (4.37) теңдікті дәлелдейік. Шынында да: |
|
x , y x, * y x, 1 y x, y x, y |
|
теорема дәлелденді. |
|
Салдар. (4.38) формуланың теңдігінен * * теңдігін |
аламыз, яғни |
ортогонал түрлендіруге ауыстырымдылық орындалады.
4.10-теоремадағы (4.38) формуланы матрицалық түрде жазайық. Ол үшін евклид R кеңістігінен:
|
li , l j |
0, |
i j |
|
|
l1 , l2 ,..., ln , |
|
i |
|
(4.39) |
|
|
|
1, |
j |
|
|
ортонормолданған базисті алайық және осы базисте сызықты түрлендіруге
75
|
a11 |
a12 |
... a1n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a21 |
a22 |
... a2n |
|
ai j |
|
|
|
|
|
|
|
|||
A |
|
, |
i, j 1, n |
||||||||||||
... ... |
... ... |
|
|
||||||||||||
|
|
|
n n |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an1 |
... ann |
|
|
|
|
|
|
|
|
|
|
|||
матрица сәйкес келсін. Онда |
|
түрлендіруінің * |
түйіндес түрлендіруіне |
||||||||||||
|
|
a11 |
a21 |
... an1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
a12 |
a22 |
... a2n |
a j ij |
|
|
|
|
|
|
|
||||
|
, i, j 1, n |
||||||||||||||
... ... |
... ... |
|
|||||||||||||
|
|
|
|
n n |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1n |
... ann |
|
|
|
|
|
|
|
|
|
|||
матрица сәйкес келеді.
4.17-анықтама. Сызықты түрлендіруінің A матрицасы ортогонал деп аталады, егер
A A 1 |
немесе A A A A E |
|
||
теңдігі орындалса, мұндағы E - бірлік матрица. |
|
|
||
Осы анықтамадан соң |
4.10-теореманы |
«матрица тілінде» тұжырымдауға |
||
болады. |
|
|
|
|
4.11-теорема. Евклид |
R |
кеңістігіндегі |
сызықты |
түрлендіруі (4.39) |
ортонормалданған базисте ортогонал болу үшін, осы түрлендірудің матрицасы ортогонал болуы:
A A 1 немесе A A A A E |
(4.40) |
қажетті әрі жеткілікті. |
|
Қажеттілігі. түрлендіруі ортогонал болсын деп ұйғарып, (4.40) |
теңдікті |
дәлелдейік. (4.38) теңдіктен |
|
* * |
|
Осыдан A A A A E болады, онда A A 1 .
Жеткіліктілігі. (4.40) теңдігі орындалды деп ұйғарып, (4.39) теңдікті дәлелдейік. (4.40) теңдіктен
A A A A E, * * .
Онда * 1 теңдігі орындалады. Теорема дәлелденді.
Жоғарыдағы теоремалардан: кез келген ортогонал түрлендірудің кері түрлендіруі бар, ал ортогонал матрицаның кері матрицасы бар.
Ортогонал түрлендірудің қасиеттері.
1. бірлік түрлендіру ортогоналды.
Дәлелдеу. x x, y y , онда x , y x, y теңдігі орындалады.
76
2. Егер мен |
|
ортогонал түрлендірулер болса, онда де ортогонал |
түрлендіру. |
|
|
Шынында да, |
|
|
x , x x , * y x , y x, y
3. Егер ортогонал түрлендіру болса, онда 1 түрлендіру де ортогонал. Дәлелдеу. ортогонал түрлендіру болғандықтан, ( * 1 ):
1 * * 1 1 1
теңдігі орындалады.
4. Егер ортогонал түрлендіру болса, онда ортогонал болуы үшін, 1 болуы қажетті әрі жеткілікті.
Дәлелдеу.
x , y 2 x , y 2 x, y
Осыдан |
|
|
|
|
|
|
|
|
|
|
|
|
x , y |
x, y |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
теңдігі орындалуы үшін, 2 1, |
|
|
1 болуы қажетті әрі жеткілікті. |
|||||||||||||||||||||||||||||
5. Егер |
ортогонал түрлендіру болса, онда ол элементтің ұзындығын ӛзгертпейді, |
|||||||||||||||||||||||||||||||
яғни |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
2 |
|
|
|
x |
|
|
|
2 , |
x R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Дәлелдеу. |
Барлық x y R үшін (4.27) теңдіктен |
|
||||||||||||||||||||||||||||||
x , x x, x , |
|
|
|
x |
|
|
|
2 |
|
|
|
x |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
теңдігін аламыз.
6. ортогонал түрлендіруінің меншікті мәні 1-ге тең. Дәлелдеу. Егер x x болса, онда
x, x x , x x, x 2 x, x
Осыдан, 2 1, 1.
7.ортогонал түрлендіруінің әртүрлі меншікті мәндерінің меншікті
элементтері ортогонал болады. |
|
|
Дәлелдеу. x 1 x, y 2 y |
және 1 1, 2 1 болсын, |
x, y 0 теңдігін |
дәлелдейік. Ол үшін x , y скаляр кӛбейтіндіні қарастырайық: |
|
|
x, y x , y 1 2 x, y
Осыдан 1 1 2 x, y 0 , мұндағы 1 1 2 0 . Онда, x, y 0 .
77

Осы сияқты R кеңістігінің ортогонал түрлендіруінің ортогонал матрицасына
тӛмендегі қасиеттер дәлелденеді. |
|
|
||
|
1. |
E бірлік матрица ортогонал. |
|
|
|
2. |
Егер A мен B матрицалары ортогонал болса, онда |
A B матрицасы да |
|
ортогонал болады. |
|
|
||
3. |
Егер A матрица ортогонал болса, онда A 1 |
ортогонал болады. |
|
|
|
|
|
|
|
|
|
A 1 A 1 A 1 A 1 A A 1 E . |
|
|
4. |
Егер |
A ортогонал болса, онда A ортогонал болуы үшін, |
1 болуы қажетті |
|
әрі жеткілікті. |
|
|
||
5. |
A ортогонал матрицаның меншікті мәндері комплекс болуы мүмкін, мысалы |
|||
|
|
cos |
sin |
|
|
|
A |
. |
|
|
|
|
|
|
|
|
sin |
cos |
|
матрицасы ортогонал, яғни A A E , ал оның меншікті мәндері комплекс сандар:
2 cos i sin
6. Егер A ортогонал матрицаның меншікті мәні нақты сан болса, онда ол 1-ге тең.
7.A ортогонал матрицаның әртүрлі меншікті мәндерінің меншікті элементтері ортогонал болады.
8.A ортогонал матрицаның анықтауышы 1-ге тең.
5. СЫЗЫҚТЫ ГЕОМЕТРИЯЛЫҚ ОБЪЕКТІЛЕР
5.1 Нҥктелердің ара қашықтығы. Кесіндіні берілген қатынаста бӛлу
Егер жазықтықта тік бұрышты XOY координаталар жүйесі берілсе, онда осы
жазықтықтың x және |
y |
координаталары бар М нүктесін – М(x;y) деп белгілейміз. |
|||||||||||||||||||
M1 x1 , y1 |
және |
M 2 x2 , y2 |
|
нүктелерінің ара |
қашықтығы d |
мына |
|||||||||||||||
формула арқылы анықталады: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
x |
2 |
|
x |
2 y |
2 |
y 2 |
|
|
|
(5.1) |
||||||
Дербес жағдайда, O 0; 0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
x, y |
|
|
||||
координаталар басынан |
M |
нүктесіне дейінгі |
d ара |
||||||||||||||||||
қашықтық: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
d |
|
|
|
|
x 2 y 2 |
|
|
|
|
(5.2) |
|||
Кесіндіні берілген қатынаста бӛлу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
AB кесіндіні берілген 0 |
қатынаста бӛлетін |
C нүктенің координаталарын |
|||||||||||||||||||
табу керек, яғни |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AC |
|
|
|
|
|
|
|
|
|
(5.3) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
CB |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Егер A (x1 , y1 , z1 ) және |
|
|
|
|
|
|
|||||||||||||||
B (x2 , y2 , z2 ) |
болса, C нүктенің белгісіз х, у және z |
||||||||||||||||||||
координаттарын табу керек. |
(5.3) |
формуладан |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
AC CB |
|
|
|
|
|
|
|
(5.4) |
|||||||||
78

дұрыстығы шығады. AC x x1 , y y1, z z1 , CB x2 x, y2 y, z2 z
(х х1 , у у1 , z z1 ) (х2 х, у2 у, z2 z)
(õ õ1 , ó2 ó1 , z2 z1 ) ( (õ2 õ), ( ó2 ó), (z2 z))
Соңғы теңдіктің координаттарын теңестіріп теңдеулер жүйесін аламыз:
х х1 (х2 |
х) |
|
|||
y y |
y |
|
|
|
|
2 |
y |
|
|||
1 |
|
|
|
||
z z z |
2 |
z |
|
||
1 |
|
|
|
||
х |
|
х1 х2 |
|
|
|||||
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
y y |
|
(5.5) |
||||
y |
|
|
|||||||
|
1 |
|
2 |
|
|
||||
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
||
|
|
|
z1 z2 |
|
|||||
z |
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
(5.5) формулалар |
|
кесіндіні берілген |
қатынаста |
бӛлу формулалары деп аталады. |
|||||
Дербес жағдайда |
1 болғанда, |
C нүктесі кесіндінің ортасында жатса, (5.5) түрі |
|||||||
мынандай болады: |
|
|
|
|
|
|
|
|
|
х |
|
х1 х2 |
, |
у |
у1 у2 |
, |
z |
z1 z2 |
(5.6) |
|
|
||||||||
|
|
|
|
|
|||||
|
2 |
|
|
2 |
|
2 |
|
||
1-мысал. А(3;8) және В(-5:14) нүктелерінің арақашықтығын табу керек.
Шешуі: Арақашықтықты есептеу формуласына нүктелердің координаттарын қоямыз: d 
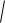 ( 5 3)2 14 8 2
( 5 3)2 14 8 2 
 64 36 10 .
64 36 10 .
2-мысал. АВ кесінді ұштары А(-2;5), В(4;17) екені белгілі. Осы кесіндінің бойынан А- ға дейінгі қашықтығы В-ға дейінгі қашықтығынан 2 есе үлкен болатын С нүктесін белгілейік. С нүктесінің координаттарын табу керек.
Шешуі: |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
AC |
CB |
|
AC |
: |
CB |
|
|
|
|||||||||||||
|
|
|
|
|
х |
2 2 4 2 , у |
|
|
5 2 7 |
13 , яғни С(2;13) . |
|||||||||||
|
|
|
|
|
c |
|
|
||||||||||||||
|
|
|
|
|
c |
|
|
|
1 2 |
|
1 |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3-мысал. |
АВ кесіндінің ортасы С(2;3) нүктесі екені белгілі. Егер В(7:5) болса, А |
||||||||||||||||||||
нүктесінің координаттарын табу керек. |
|
|
|
|
|
||||||||||||||||
Шешуі: х |
х1 х2 |
, у |
у1 |
у2 |
формуласы бойынша |
||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
xA 7 |
|
|
xA 3, 3 |
|
y A 5 |
y A 1 |
||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
яғни А(-3;1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.2. Полярлық координаталар |
|
|
P жазықтығында тікбұрышты координаталар жүйесі берілсін. Яғни О |
полюсі мен |
|
OX және OY осьтері анықталсын. Осы жүйемен тығыз байланысты |
тағы |
да бір |
полярлық деп аталатын координаталар жүйесі бар. Жазықтықтағы кез келген |
A x.y |
|
нүктесінің орны келесі екі , жұбы нақты сандарымен толық сипатталады.
Осы сандардың , жұбы A нүктесінің полярлық координатасы деп аталады.
79

Декарттық координаталарды полярлық координаталар арқылы ӛрнектеу
формуласы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x cos |
y sin |
(5.7) |
||||
Керісінше полярлық координаталарды декарттық координаталар арқылы |
||||||||||||
ӛрнектеу формуласы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
y |
|
|
|
åãåð x o |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x |
|
|
|
|||
|
|
2 |
y |
2 |
|
|
|
|
|
|||
x |
|
|
|
|
|
(5.8) |
||||||
|
|
|
|
|
y |
|||||||
|
|
|
|
|
|
|
|
|
|
åãåð x 0 |
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
arctg |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
x |
|
|
5.3. Жазықтықтағы тҥзудiң теңдеулерi
Жазықтықтағы тiк бұрышты координат жүйесiнде L түзуi берiлсiн. Басы O нүктеде
жатқан |
|
векторының соңғы нүктесiнен осыған перпендикуляр |
L түзуi |
жүргiзiлген |
||||
a |
||||||||
(5.1-сурет). Сондықтан |
|
векторы L түзуiн толық анықтайды. |
p |
саны |
|
вектордың |
||
a |
a |
|||||||
ұзындығы |
|
|
|
|
|
|
|
векторы |
|
векторының |
бiрлiк |
p | a | . Мұндағы |
n (cos ,cos ) |
a |
|||||||||
векторы. |
|
|
|
|
|
|
|
|
|
|
|
және |
|
бұрыштары |
|
|
|
|
|
|
|
|
|
n векторының |
|
|
|
|
|||||||
Ox және |
Oy |
ӛстерімен |
жасайтын |
|
|
|
|
||||
бұрыштары |
cos2 cos2 1. . |
M x, y |
|
|
|
|
|||||
нүктесi L түзудiң кез келген |
нүктесi, |
|
|
|
|
||||||
оның радиус |
векторын |
r x, |
y |
деп |
|
|
|
|
|||
белгiлеймiз. |
L |
түзудiң |
кез |
келген |
|
|
|
|
|||
нүктесiнiң радиус векторының |
|
бiрлiк |
|
|
|
|
|||||
n |
|
|
|
|
|||||||
вектор бағытындағы проекциясы тұрақты |
|
|
|
|
|||||||
және ол p -ға тең. Сонымен |
|
|
|
5.1-сурет |
|
||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
( p 0) |
|
|
(5.9) |
|
|
|
|
|
(r , n) p |
|
|
|||||
(5.9) теңдеу жазықтықтағы |
L түзудiң векторлық теңдеуi деп аталады. Бұл теңдеу |
||||||||||
координаттар арқылы былай жазылады |
|
|
|
|
|
||||||
|
|
|
x cos y cos p |
( p 0) |
(5.10) |
||||||
теңдеудi жазықтықтағы L түзудiң нормаль түріндегі теңдеуі деп аталады. |
|
||||||||||
Сонымен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax By C 0 |
|
|
|
(5.11) |
||
(5.11) теңдеу жазықтықтағы түзудiң жалпы түрдегі теңдеуі деп аталады.
Бұл теңдеудi әрқашанда нормальді түрге келтіруге болады оны мына санға кӛбейтiп
|
|
|
1 |
|
. |
(5.12) |
|
|
|
|
|
||||
|
|
|
|
||||
A2 |
B2 |
||||||
|
|
|
|
|
80
