
- •Долгіх, В. М.
- •1. МАТРИЦІ Й ВИЗНАЧНИКИ
- •1.1. МАТРИЦІ. ВИДИ МАТРИЦЬ
- •Види матриць
- •Деякі властивості добутку матриць
- •Властивості транспонування матриці
- •1.3. ВИЗНАЧНИКИ
- •Властивості визначників
- •1.4. ОБЕРНЕНА МАТРИЦЯ
- •Обчислення оберненої матриці методом елементарних перетворень
- •1.5. РАНГ МАТРИЦІ
- •1.5. РАНГ МАТРИЦІ
- •Обчислення рангу матриць методом елементарних перетворень
- •Поняття про лінійну залежність і незалежність рядків матриці
- •1.6. ПРИКЛАДИ ЗАСТОСУВАННЯ МАТРИЦЬ В ЕКОНОМІЦІ
- •Таблиця 1.1
- •Таблиця 1.2
- •Таблиця 1.3
- •Питання для самоперевірки
- •1.7. Вправи
- •2. СИСТЕМИ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ
- •2.1. ОСНОВНІ ОЗНАЧЕННЯ
- •2.2. СХЕМА ДОСЛІДЖЕННЯ СИСТЕМ. ТЕОРЕМА КРОНЕКЕРА-КАПЕЛЛІ
- •Схема дослідження систем
- •2.3. МЕТОД ГАУССА (метод послідовного виключення невідомих)
- •2.4. МЕТОД ЖОРДАНА-ГАУССА (метод повного виключення невідомих)
- •2.5. СИСТЕМИ ЛІНІЙНИХ ОДНОРІДНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ
- •Однорідні системи n-го порядку (n рівнянь із n невідомими)
- •2.6. СИСТЕМИ n ЛІНІЙНИХ РІВНЯНЬ ІЗ n НЕВІДОМИМИ
- •2.6.1. Матричний метод розв’язування систем (метод оберненої матриці)
- •2.6.2. Розв’язування систем методом Крамера
- •2.7. ВЛАСНІ ВЕКТОРИ ТА ВЛАСНІ ЧИСЛА МАТРИЦІ
- •2.8. ПРИКЛАДИ ЗАСТОСУВАННЯ СИСТЕМ В ЕКОНОМІЦІ
- •Таблиця 2.1
- •Таблиця 2.2
- •Питання для самоперевірки
- •2.9. Вправи
- •Таблиця 2.3
- •Таблиця 2.4
- •Таблиця 2.5
- •3. ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ
- •3.1. ОСНОВНІ ОЗНАЧЕННЯ
- •3.3. ЛІНІЙНА НЕЗАЛЕЖНІСТЬ ВЕКТОРІВ
- •3.4. БАЗИС. РОЗКЛАДАННЯ ВЕКТОРА ЗА БАЗИСОМ
- •Лінійні операції над векторами в координатній формі
- •3.5. АФІННА СИСТЕМА КООРДИНАТ
- •3.6. ПРОЕКЦІЯ ВЕКТОРА НА ВІСЬ
- •3.7. ВЕКТОРИ В ОРТОНОРМОВАНОМУ БАЗИСІ. ДЕКАРТОВА ПРЯМОКУТНА СИСТЕМА КООРДИНАТ
- •Лінійні операції над векторами в базисі
- •3.8. НАПРЯМНІ КОСИНУСИ ВЕКТОРА
- •3.9. ПОДІЛ ВІДРІЗКА В ЗАДАНОМУ ВІДНОШЕННІ
- •3.10. СКАЛЯРНИЙ ДОБУТОК ВЕКТОРІВ
- •3.10. СКАЛЯРНИЙ ДОБУТОК ВЕКТОРІВ
- •Алгебраїчні властивості скалярного добутку
- •Геометричні властивості скалярного добутку
- •Скалярний добуток в ортонормованому базисі
- •Деякі важливі формули
- •3.11. ВЕКТОРНИЙ ДОБУТОК ВЕКТОРІВ
- •Алгебраїчні властивості векторного добутку
- •Геометричні властивості векторного добутку
- •Векторний добуток в ортонормованому базисі
- •3.12. МІШАНИЙ ДОБУТОК ВЕКТОРІВ
- •Основна алгебраїчна властивість мішаного добутку
- •Геометричні властивості мішаного добутку
- •Мішаний добуток в ортонормованому базисі
- •Лінійні операції над векторами
- •3.13.2. Лінійна незалежність векторів. Базис і координати
- •3.13.3. Евклідів n-вимірний простір En
- •Алгебраїчні властивості скалярного добутку
- •Кут між векторами в евклідовому просторі En
- •Таблиця 3.1
- •Питання для самоперевірки
- •3.14. Вправи
- •4. АНАЛІТИЧНА ГЕОМЕТРІЯ НА ПЛОЩИНІ
- •4.1. СИСТЕМИ КООРДИНАТ НА ПЛОЩИНІ
- •4.1.1. Декартова прямокутна система координат
- •4.1.2. Полярна система координат
- •Зв’язок між полярними та прямокутними декартовими координатами точки
- •4.1.3. Перетворення системи координат
- •Паралельне перенесення осей
- •4.2. ЛІНІЯ НА ПЛОЩИНІ. ОСНОВНІ ОЗНАЧЕННЯ
- •Параметричні рівняння лінії
- •Таблиця 4.1
- •Лінія в полярних координатах
- •Таблиця 4.2
- •4.3. ПРЯМА НА ПЛОЩИНІ
- •4.3.1. Різні форми рівнянь прямої
- •Умови паралельності й перпендикулярності двох прямих
- •4.3.3. Нормальне рівняння прямої
- •Ознаки нормального рівняння
- •4.3.4. Відстань від точки до прямої
- •4.3.5. Приклади розв’язування задач
- •4.3.6. Приклади застосування лінійної залежності в економіці
- •Лінійна залежність між витратами й обсягом виробництва продукції
- •Питання для самоперевірки
- •4.3.7. Вправи
- •4.4. АЛГЕБРАЇЧНІ ЛІНІЇ ДРУГОГО ПОРЯДКУ НА ПЛОЩИНІ
- •4.4.1. Основні поняття
- •4.4.2. Коло
- •4.4.4. Гіпербола
- •4.4.6. Криві другого порядку. Узагальнення
- •Питання для самоперевірки
- •4.4.7. Вправи
- •5. АНАЛІТИЧНА ГЕОМЕТРІЯ У ПРОСТОРІ
- •5.1. ПЛОЩИНА У ПРОСТОРІ R3
- •5.1.1. Різні форми рівнянь площини
- •Ознаки нормального рівняння
- •5.1.2. Відхилення та відстань точки від площини
- •5.1.3. Кут між двома площинами. Умови паралельності та перпендикулярності двох площин
- •5.1.4. Приклади розв’язування задач
- •5.2. ПРЯМА У ПРОСТОРІ R3
- •5.2.1. Різні форми рівнянь прямої
- •5.2.3. Відстань від точки до прямої у просторі R3
- •5.2.4. Відстань між паралельними прямими у просторі R3
- •5.2.5. Відстань між перехресними прямими у просторі R3
- •Умови паралельності й перпендикулярності прямої та площини
- •Питання для самоперевірки
- •5.2.7. Вправи
- •5.3. АЛГЕБРАЇЧНІ ПОВЕРХНІ ДРУГОГО ПОРЯДКУ
- •5.3.1. Загальне рівняння поверхні другого порядку
- •5.3.2. Еліпсоїд. Сфера
- •5.3.3. Однопорожнинний гіперболоїд
- •5.3.4. Двопорожнинний гіперболоїд
- •5.3.5. Конус другого порядку
- •5.3.6. Еліптичний параболоїд
- •5.3.7. Гіперболічний параболоїд
- •5.3.8. Циліндри
- •Питання для самоперевірки
- •5.3.9. Вправи
- •СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ

27. Знайти точку N, симетричну точці A(4; 1; 6) відносно прямої
ìx - y - 4z +12 = 0,
í
î2x + y - 2z + 3 = 0.
28.Знайти точку N, симетричну точці A(2; – 5; 7) відносно прямої, яка проходить через точки B(5; 4; 6) і C(– 2; – 17; – 8).
29.Знайти точку N, симетричну точці М(1; 2; 3) відносно площини
х+ у + 2z – 6 = 0.
30.Обчислити відстань від точки М(1; – 1; – 2) до прямої
x + 3 = y + 2 = z - 8 . |
||
3 |
2 |
- 2 |
31. Довести паралельність прямих і знайти відстань між ними:
x -1 |
|
y +1 |
|
z |
|
ì |
x + y - z = 0, |
= |
= |
і |
í |
|
|||
3 |
|
|
|
||||
|
- 2 1 |
|
îx - y - 5z - 8 = 0. |
||||
32. Знайти відстань між прямими:
ì x + y - z -1 = 0, |
i |
ì x + 2 y - z - 2 = 0, |
||
í |
= 0 |
í |
= 0. |
|
î2x + y - z - 2 |
|
îx + 2 y + 2z + 4 |
||
5.3. АЛГЕБРАЇЧНІ ПОВЕРХНІ ДРУГОГО ПОРЯДКУ
5.3.1. Загальне рівняння поверхні другого порядку
Поверхнею другого порядку називається множина точок простору R3, координати котрих задовольняють алгебраїчне рівняння другого степеня
Ax2 + By2 + Cz2 + 2Dxy + 2Eyz + 2Fxz + 2Gx + 2Hy + 2Kz + L = 0, (5.32)
де хоча б один із коефіцієнтів A, B, C, D, E, F відмінний від нуля.
Це рівняння може визначати сферу, еліпсоїд, гіперболоїд (однопорожнинний або двопорожнинний), параболоїд (еліптичний або гіперболічний), конус, циліндр (еліптичний, гіперболічний або параболічний), а також вироджену поверхню другого порядку(порожню множину, точку, площину, пару площин).
За допомогою паралельного переносу й повороту системи координат рівняння (5.32) можна звести до канонічного вигляду.
Форму поверхонь вивчають методом перерізів. Для цього перетинають поверхню площинами, паралельними координатним площинам, і визначають тип кривої, що виходить при цьому перетині.
ДВНЗ “Українська академія банківської справи НБУ”
117
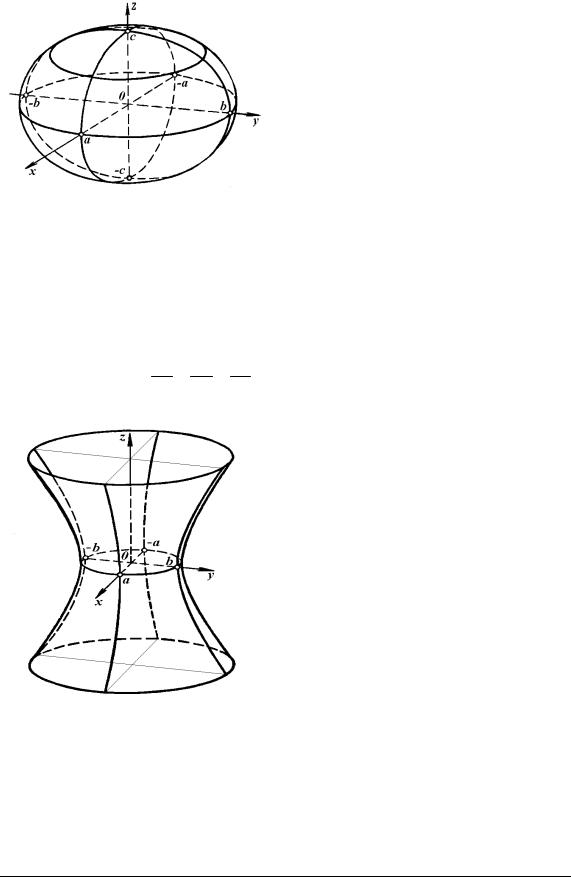
5.3.2. Еліпсоїд. Сфера
|
|
Канонічне |
рівняння еліпсоїда |
||||
з півосями a, b, c (рис. 5.10): |
|||||||
|
x2 |
+ |
y 2 |
+ |
z 2 |
=1 |
(a, b, c > 0).(5.33) |
|
a2 |
b2 |
|
||||
|
|
|
c2 |
|
|||
При a = b = c = R рівняння (5.33) перетворюється в рівняння сфери з центром у початку координат і радіусом R:
Рис. 5.10. Еліпсоїд |
x2 |
+ y2 + z 2 |
= R 2. |
(5.34) |
|
|
|
|
Рівняння сфери з центром у точці M0(x0, y0, z0) і радіусом R:
(x - x0 )2 + ( y - y0 )2 + (z - z0 )2 = R 2. |
(5.35) |
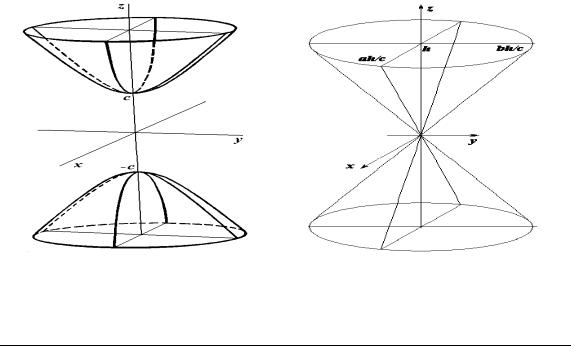
5.3.3. Однопорожнинний гіперболоїд
Канонічне рівняння однопорожнинного гіперболоїда
x2 + y2 - z2 a2 b2 c2
Рис. 5.11.
Однопорожнинний
гіперболоїд
=1 (a, b, c > 0). |
|
|
|
(5.36) |
|||||
Поверхня |
симетрична |
відносно |
|||||||
координатних |
площин xOz |
і yOz. |
|||||||
Початок координат є центром симе- |
|||||||||
трії (рис. 5.11). |
|
|
|
|
|
||||
Перерізи |
поверхні (5.36) пло- |
||||||||
щинами х = 0, y = 0 є гіперболами: |
|||||||||
|
y 2 |
- |
z 2 |
|
=1, |
x2 |
- |
z 2 |
=1. |
|
b2 |
c2 |
a2 |
c2 |
|||||
|
|
|
|
|
|||||
Переріз поверхні площиною z = h є еліпсом
x2 |
+ |
y2 |
=1+ |
h2 |
= H2 Þ |
x2 |
+ |
y2 |
=1. |
|
a2 |
b2 |
c2 |
(aH)2 |
(bH)2 |
||||||
|
|
|
|
|
Однопорожнинний гіперболоїд належить до лінійчатих поверхонь. Він може бути побудований за -до помогою двох систем прямих ліній.
ДВНЗ “Українська академія банківської справи НБУ”
118
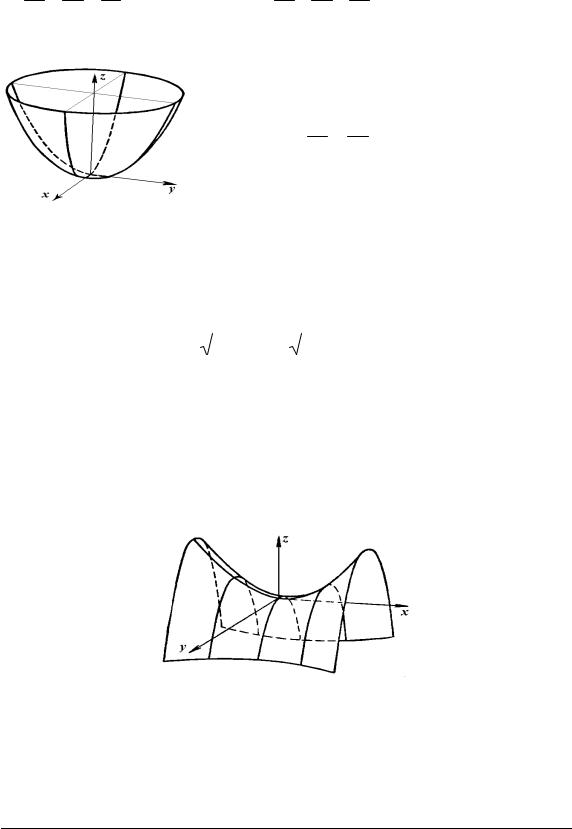
5.3.4. Двопорожнинний гіперболоїд
Канонічне рівняння двопорожнинного гіперболоїда:
- |
x2 |
- |
y2 |
+ |
z 2 |
= 1 (a, b, c > 0). |
(5.37) |
|
a2 |
b2 |
c2 |
||||||
|
|
|
|
|
Поверхня симетрична відносно координатних осей і координатних площин. Центр симетрії знаходиться у початку координат (рис. 5.12).
Перерізи поверхні площинами х = 0 і y = 0 є гіперболами:
- |
y2 |
+ |
z 2 |
=1 |
(b, c > 0); - |
x2 |
+ |
z 2 |
= 1 (a, c > 0). |
|
b2 |
c2 |
a2 |
c2 |
|||||||
|
|
|
|
|
|
5.3.5. Конус другого порядку
Конічною поверхнею називається поверхня, яку описує пряма (твірна), що проходить через фіксовану точкуS (вершину конуса) і змінну точку M, яка рухається уздовж кривої (напрямної конічної поверхні). Якщо напрямною конічної поверхні є крива другого порядку, то поверхня називається конусом другого порядку.
Канонічне рівняння еліптичного конуса другого порядку:
|
x2 |
|
+ |
y2 |
|
- |
z 2 |
= 0 |
(a, b, c > 0). |
(5.38) |
|||||
|
a2 |
|
b2 |
|
|
||||||||||
|
|
|
|
|
c2 |
|
|
|
|
|
|||||
Поверхня симетрична відносно координатних осей і координатних |
|||||||||||||||
площин. Центр симетрії знаходиться у початку координат (рис. 5.13). |
|||||||||||||||
Перерізи конуса |
|
площинамих |
= 0 і y = 0 є |
прямими: |
|||||||||||
y = ±bz / c, x = ±az / c. Перерізи поверхні площинами z = h є еліпсами: |
|||||||||||||||
|
|
|
x2 |
|
+ |
y 2 |
=1 |
(H 2 = |
h2 |
). |
|
||||
|
|
(aH )2 |
|
(bH )2 |
|
|
|||||||||
|
|
|
|
|
|
|
c2 |
|
|||||||
Рис. 5.12. Двопорожнинний |
Рис. 5.13. Еліптичний конус |
гіперболоїд |
другого порядку |
ДВНЗ “Українська академія банківської справи НБУ”
119
Рівняння еліптичних конічних поверхонь другого порядку, осі яких співпадають з осями Ox, Oy, мають вигляд:
|
параболоїд |
|
у = 0 є параболами: |
|
|
|
|||||
|
|
|
|
y2 |
= 2qz, x2 |
= 2 pz. |
|
||||
- x2 |
+ y2 |
+ z 2 = 0 |
(a, b, c > 0), |
x2 |
- y2 |
+ z 2 |
= 0 |
(a, b, c > 0). (5.39) |
|||
a2 |
b2 |
c2 |
|
|
a2 |
b2 |
|
c2 |
|
|
|
|
|
|
5.3.6. Еліптичний параболоїд |
|
|
||||||
|
|
|
|
Канонічне рівняння еліптичного пара- |
|||||||
|
|
|
|
болоїда: |
|
x2 |
|
y2 |
|
|
|
|
|
|
|
|
|
p |
+ |
q |
= 2z |
( p, q > 0). |
(5.40) |
|
|
|
|
Поверхня симетрична відносно коорди- |
|||||||
|
|
|
|
натних площин xOz, yOz і вісі Oz (рис. 5.14). |
|||||||
Рис. 5.14. Еліптичний |
Перерізи |
поверхні |
площинамих |
= 0, |
|||||||
|
|
|
|
|
|
|
|
||||
Перерізи поверхні площинами z = h > 0 є еліпсами:
|
x 2 |
|
y 2 |
||||
|
|
|
+ |
|
|
|
= 1. |
( |
|
)2 |
( |
|
)2 |
||
2 ph |
2qh |
||||||
5.3.7. Гіперболічний параболоїд
Рівняння гіперболічного параболоїда:
|
x 2 |
y 2 |
|
(5.41) |
||
|
|
- |
|
= 2 z |
( p , q > 0 ) . |
|
|
|
|||||
|
p |
q |
|
|
||
Поверхня симетрична |
відносно |
координатних |
площинxOz, yOz |
|||
(рис. 5.15). |
|
|
|
|
||
Рис. 5.15. Гіперболічний параболоїд
1. У перерізі поверхні площиноюx = 0 одержуємо параболу: y2 = -2qz. Вітки параболи направлені вниз.
2. У перерізі поверхні площиноюy = 0 одержуємо параболу: x2 = 2 pz. Вітки параболи направлені нагору.
ДВНЗ “Українська академія банківської справи НБУ”
120
