Рівняння сторони AD:
y - yA = kAD (x - xA ),
|
|
y - 3 = 3(x + 2), |
y = 3x + 9. |
|||
|
|
Рівняння |
сторони BC, |
що |
проходить |
|
|
|
через точку C паралельно AD: |
|
|||
|
Рис. 4.20 |
y - yC = kBC (x - xC ), |
|
|||
|
|
|
kBC = kAD = 3, |
|
|
|
|
|
y - 5 = 3(x - 2), Þ y = 3x - 1. |
||||
З |
умови |
перпендикулярності |
сторінAB |
і |
BC |
знаходимо: |
kAB = -1/kBC = -1/3. Сторони DC і AB |
паралельні: kDC = kAB = -1/3. |
|||||
Рівняння сторін AB і DC: |
|
|
|
|
||
AB: y - yA = k AB (x - xA ), y - 3 = -(1/ 3)(x + 2), x + 3y - 7 = 0; |
||||||
DC: |
y - yC = kDC (x - xC ), y - 5 = -(1/ 3)(x - 2), x + 3y - 17 = 0. < |
|||||
4.3.6. Приклади застосування лінійної залежності в економіці
Лінійна залежність між витратами й обсягом виробництва продукції
Усі витрати підприємства на виробництво й збут продукції складаються зі сталих (орендна плата, амортизація та ін.) та змінних (пряма заробітна плата, витрати сировини, палива, електроенергії та ін.). Якщо змінні витрати пропорційні обсягу виробництва продукції(послуг) x, то сума витрат на виробництво продукції (послуг) y:
|
|
y = kx + b, |
(4.33) |
де b |
– |
сума сталих витрат; |
|
k |
– |
ставка змінних витрат на одиницю продукції(послуг). |
|
Приклад 4.21. Скласти лінійну залежність повних витратy на виробництво продукції від обсягу виробництваx, якщо при максимальному обсязі виробництва продукції xmax = 2 000 од. загальні витрати
= 250 млн. грн. Мінімальному обсягу виробництва xmin =1 500 од. відповідають загальні витрати ymin = 200 млн. грн.
► Застосуємо рівняння прямої, що проходить через дві задані точки:
y - ymin |
= |
x - xmin |
Þ |
y - 200 |
= |
x -1500 |
|
Þ y = 0,1x + 50. |
ymax - ymin |
xmax - xmin |
|
2 000 -1500 |
|||||
|
250 - 200 |
|
||||||
ДВНЗ “Українська академія банківської справи НБУ”
88
Сума сталих витрат 50 млн. грн., змінні витрати на одиницю продукції – 100 000 грн. <
Приклад 4.22. Підприємство виробляє 1 000 виробів. Кожен виріб реалізується за вартістю 20 000 (0,02 млн.) грн. Сталі витрати на виробництво – 4 млн. грн., змінні витрати на одиницю продукції– 12 000 (0,012 млн.) грн.
Скласти лінійні залежності доходуY від реалізації продукції та повних витрат на виробництво y від обсягу виробництва x. Знайти залежність прибутку P від обсягу виробництва x, максимальний прибуток, мінімальний обсяг прибуткового виробництва, обсяг реалізації, при якому прибуток дорівнює 2 млн. грн.
► Залежність доходу Y від обсягу реалізації продукції x: Y = 0,02x (млн. грн.).
Залежність повних витрат на виробництво y від обсягу виробниц-
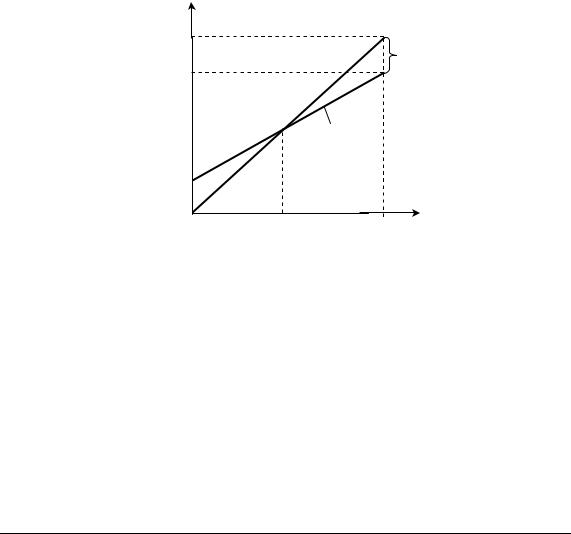
тва x (рис. 4.21):
y = 0,012 x + 4 (млн. грн.).
y, млн. грн. |
|
20 |
P |
Y = 0,02x |
|
16 |
|
12
y = 0,012x + 4
8
4
0 |
500 |
1 000 x |
Рис. 4.21. Залежності доходу Y і повних витрат y від обсягу виробництва x
Залежність прибутку P від обсягу виробництва (реалізації) x:
P = Y - y = 0,02x - (0,012x + 4) = 0,008x - 4 (млн. грн.).
Максимальний прибуток при реалізації 1 000 виробів:
Pmax = 0,008×1 000 - 4 = 4 (млн. грн.).
Виробництво прибуткове, якщо прибуток P > 0:
P = 0,008x - 4 > 0 Þ x > |
4 |
= 500 од., |
|
||
0,008 |
|
|
тобто мінімальний обсяг прибуткового виробництва xmin = 501 од.
ДВНЗ “Українська академія банківської справи НБУ”
89