r |
r |
r |
назива- |
Якщо хоча б одне із чисел сk ¹ 0, то вектори a1 |
, a2 |
, ..., an |
ються лінійно залежними, оскільки принаймні один із векторів можна подати у вигляді лінійної комбінації інших, наприклад, при с1 ¹ 0:
r |
r |
r |
, |
li = -ci c1 |
(i = 2, 3, ..., n). |
(3.3) |
a1 |
= l2a2 |
+ ... + ln an |
Максимальна кількість лінійно незалежних векторів простору на-
зивається розмірністю простору.
Істинні такі твердження:
1.Будь-які два колінеарні вектори лінійно залежні (рис. 3.7).
2.Будь-які три компланарні вектори лінійно залежні (рис. 3.8).
3.Будь-які чотири вектори у тривимірному просторі лінійно залежні.
|
|
r |
|
|
|
|
|
a |
l2c |
|
r |
r |
r |
|
|
|||||
|
|
|
a |
= l1b + l2c |
||
|
r |
|
|
|
|
|
r |
r |
r |
|
|
|
|
b = la |
c |
|
|
|
|
|
rr
b l1b
Рис. 3.7 |
Рис. 3.8 |
3.4. БАЗИС. РОЗКЛАДАННЯ ВЕКТОРА ЗА БАЗИСОМ
Упорядкована сукупність n лінійно незалежних векторівn-вимір- ного простору Rn називається базисом.
Базисом на прямій (у R1) називається будь-який ненульовий вектор. Базисом на площині (у R2) називаються два упорядковані неколі-
неарні вектори.
Базисом у тривимірному просторі(R3) називаються три упоряд-
ковані некомпланарні вектори.
Якщо базисні вектори взаємно перпендикулярні(ортогональні), базис називають ортогональним. Ортонормованим називають ортогональний базис, утворений одиничними векторами.
r
Якщо вектор a поданий у вигляді лінійної комбінації базисних векторів:
то |
кажуть, |
що |
|
r |
r |
|
r |
c1e1 |
, c2 e2 |
, c3e3 |
|
числа c1 , c2 , c3
r
пишуть так: a =
r |
r |
r |
r |
, |
|
|
|
|
|
|
(3.4) |
a |
= c1e1 |
+ c2e2 |
+ c3e3 |
r |
r |
|
r |
|
|||
він розкладений |
за |
|
|
. |
Вектори |
||||||
базисомe , e |
2 |
, e |
3 |
||||||||
|
|
|
|
|
1 |
|
|
|
r |
||
називають складовими (компонентами) вектора a , а |
|||||||||||
- його координатами в базисі |
r |
r |
|
r |
|
Зазвичай |
|||||
e1 , |
e 2 |
, e |
3 . |
||||||||
(c1 , c2 , c3 ).
ДВНЗ “Українська академія банківської справи НБУ”
51
r |
|
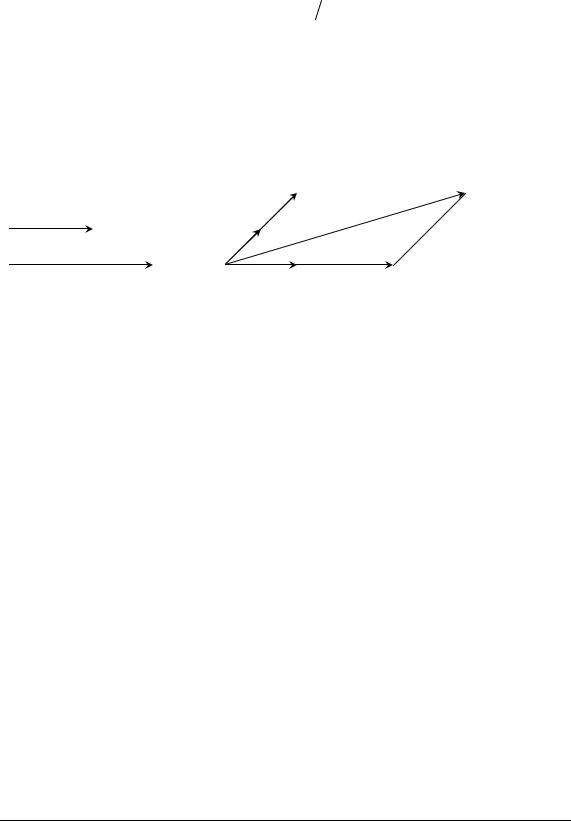
На |
рис. |
3.9 наведено |
приклад |
розкладу |
вектораa за базисом |
||||||||
, |
r |
Координатами вектора a є числа (3, 2), а складовими - векто- |
|||||||||||||
e1 |
e2 . |
||||||||||||||
|
|
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
ри 3e1 і |
2e2 . |
r |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2e2 |
|
|
|
|
|
|
r |
r |
r |
|
||
|
|
|
r |
|
|
|
|
|
|
|
|
a = 3e1 |
+ 2e2 |
= (3, 2) |
|
|
|
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
e1 |
|
|
|
|
3e1 |
|
|
|
r |
r |
|
|
|
|
Рис. 3.9. Розклад вектора a за базисом e1, |
e2 |
|||||||||||
|
|
Лінійні операції над векторами в координатній формі |
|||||||||||||
|
|
Нехай у базисі |
r |
r |
|
r |
дані вектори: |
|
|
|
|||||
|
|
e1 |
, e2 |
, e3 |
|
|
|
||||||||
|
r |
|
r |
r |
r |
= (a1, a2 , a3 ), |
r |
r |
r |
r |
= (b1, b2 , b3 ). |
||||
|
a |
= a1e1 + a2e2 + a3e3 |
b = b1e1 + b2e2 |
+ b3e3 |
|||||||||||
|
|
Тоді лінійні операції визначаються так: |
|
|
|
||||||||||
|
|
r |
r |
|
r |
|
|
|
|
r |
|
r |
± b1, a2 ± b2 , a3 ± b3 ), |
||
|
|
a ± b = (a1 ± b1 )e1 |
+ (a2 ± b2 )e2 + (a3 |
± b3 )e3 = (a1 |
|||||||||||
|
|
|
r |
|
r |
|
|
r |
r |
|
|
|
|
(3.5) |
|
|
|
|
la |
= la1e1 + la2e2 +la3e3 = (la1, la2 , la3 ). |
|
||||||||||
Приклад 3.1. Визначити, чи є лінійно залежними вектори:
r
a= (2, 3, 1), b = (– 1, 5, 6), с = (5, 1, – 4).
►Вектори лінійно залежні, якщо існують такі, одночасно не рів-
r |
r |
r |
r |
ні нулю числа c1, c2, c3, що c1a |
+ c2b + c3c |
= 0. Маємо: |
|
c1(2, 3, 1) + c2(– 1, 5, 6) + c3(5, 1, –4) = (0, 0, 0) Û |
|||
Û (2c1 – c2 + 5c3, 3c1 + 5c2 + c3, c1 + 6c2 – 4c3) = (0, 0, 0). |
|||
Звідси отримаємо систему лінійних однорідних рівнянь: |
|||
|
ì2c |
- c |
+ 5c =0, |
2 |
-1 |
5 |
|
|
|
|
|
|
ï |
1 |
2 |
3 |
3 |
5 |
1 |
= -40-1+90- (25+12+12) = 0. |
|||
|
í3c1 +5c2 + c3 = 0, Þ D = |
||||||||||
|
ïc |
+ 6c |
- 4c =0 |
1 |
6 - 4 |
|
|
|
|
||
|
î 1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
Однорідна система має ненульові розв’язки, якщо її визначник |
||||||||||
дорівнює нулю. Отже, вектори лінійно залежні. < |
r |
|
|||||||||
|
Приклад 3.2. Показати, |
|
|
|
r |
= (1, 2, |
3, 1), |
||||
|
що вектори a |
3), b = (1, |
|||||||||
r |
(1, 2, 1) утворюють |
базис |
уR3 і |
знайти |
координати |
вектора |
|||||
с |
= |
||||||||||
r
d = (3, 7, 5) у цьому базисі.
ДВНЗ “Українська академія банківської справи НБУ”
52