
- •Векторна алгебра
- •Системи лінійних алгебраїчних рівнянь. Метод послідовного виключення невідомих (метод Гаусса).
- •Поняття вектора, лінійні операції над векторами.
- •Поняття лінійно залежних і лінійно незалежних систем векторів.
- •Геометрична інтерпретація поняття лінійної залежності.
- •Поняття базису простору і площини
- •Афінна система координат.
- •Додатковий матеріал з векторної алгебри
- •Поняття лінійного простору.
- •Найпростіші властивості векторного простору.
- •Теорія визначників n-го порядку.
- •Перестановки з n символів.
- •Підстановки n-го степеня.
- •Поняття і властивості визначника n-го порядку
- •Мінори і алгебраїчні доповнення визначника
- •Лема до теореми Лапласа. Теорема Лапласа.
- •Застосування теорії визначників до лінійних систем алгебраїчних рівнянь. Теорема Крамера та лема до неї
- •Векторний простір
- •Подальше вивчення векторного простору.
- •Поняття рангу системи векторів.
- •Поняття рангу матриці. Теорема про ранг матриці.
- •Загальна теорія лінійно-алгебраїчних рівнянь
- •Критерій сумісності лінійних алгебраїчних рівнянь
- •Критерій визначеності і невизначеності системи
- •Однорідна система рівнянь. Фундаментальна система розв'язків однорідної системи рівнянь.
- •Зв’язок між розв’язком неоднорідної і відповідної однорідної системи рівнянь.
- •Алгебра матриць
- •Множиння матриць.
- •Матриці обернені до даних. Умови їх існування.
- •Операції додавання і множення на число.
- •Скалярні матриці.
- •Операції над прямокутними матрицями.
- •Псевдообернені матриці.
- •Комплесні числа.
- •Побудова множини комплексних чисел.
- •Полярна система координат.
- •Тригонометрична форма комплексного числа. Операції множення та ділення в тригонометричній формі.
- •Операції піднесення до степеня
- •Операція здобуття кореняn-ого степеня з комплексного числа
- •Кореніn-ого степеня з одниці
- •Комплексно-спряжені числа
- •Нерівність трикутника
- •Література
Геометрична інтерпретація поняття лінійної залежності.
З’ясуємо геометричний зміст поняття лінійної залежності.
Теорема 1. Для того, щоб система з одного вектора була лінійно залежною, необхідно і достатньо, щоб цей вектор був нульовим.
Теорему 1 було обґрунтовано у зауваженні попереднього параграфу.
Теорема 2. Необхідною і достатньою умовою лінійної залежності двох векторів є їх колінеарність.
Доведення.
Необхідність.
Припустимо, що вектори ![]() утворюють лінійно залежну систему.
утворюють лінійно залежну систему.
Доведемо, що вектори колінеарні.
Отже
один з векторів є лінійною комбінацією.
Нехай це ![]() (для визначеності). Тоді
(для визначеності). Тоді ![]() ,
тобто вектори колінеарні.
,
тобто вектори колінеарні.
Достатність.
Припустимо, що ![]() .
Покажемо, що система лінійно залежна.
.
Покажемо, що система лінійно залежна.
Можливі випадки:
1) Принаймні один з векторів нульовий. Тоді твердження очевидне, тому що в системі міститься лінійно залежна підсистема.
2)Обидва вектори ненульові.
Для доведення потрібна такалема.
Лема.
Якщо ![]() і
і ![]() ,
то
,
то ![]() :
:
![]() .
.
Дійсно,
якщо ![]() ,
то
,
то ![]() ,
якщо
,
якщо ![]() ,
то
,
то ![]() .
.
Згідно
із лемою маємо, що ![]() .
Таким чином система лінійно залежна.
.
Таким чином система лінійно залежна.
Теорему доведено.
Теорема 3. Необхідною і достатньою умовою лінійної залежності трьох векторів є їх компланарність.
Доведення.
Необхідність.
Припустимо, що вектори ![]() утворюють лінійно залежну систему.
Покажемо, що вони компланарні.
утворюють лінійно залежну систему.
Покажемо, що вони компланарні.
Якщо
серед векторів системи пара колінеарних,
то очевидно, що вони є компланарними.
Нехай тоді вектори попарно неколінеарні.
Тоді за означенням 1 лінійної залежності
існує вектор (наприклад, ![]() ),
що є лінійною комбінацією інших
),
що є лінійною комбінацією інших ![]() .
.
Візьмемо
точку Аі
прикладемо до неївектори ![]() .Побудуємо паралелограм зі сторонами
.Побудуємо паралелограм зі сторонами![]() .
.
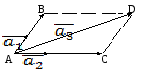
(для
визначеності
![]() )
)
Тоді
з попередньої рівності випливає, що ![]() – сторони і діагональ паралелограма.
Отже ці вектори компланарні. Оскільки
– сторони і діагональ паралелограма.
Отже ці вектори компланарні. Оскільки
![]() ,
то вектори
,
то вектори![]() також компланарні.
також компланарні.
Достатність.
Припустимо, що ![]() – компланарні. Покажемо, що вони лінійно
залежні.
– компланарні. Покажемо, що вони лінійно
залежні.
Якщо серед векторів системи пара колінеарних, то в системі є лінійно залежна підсистема і тому вся система залежна. Нехай тоді вектори попарно неколінеарні.
Прикладемо вектори ![]() до однієї точки А і побудуємо паралелограм
ABDCздіагоналлю
до однієї точки А і побудуємо паралелограм
ABDCздіагоналлю
![]() і сторонами, що знаходяться на прямих,
на яких знаходяться вектори
і сторонами, що знаходяться на прямих,
на яких знаходяться вектори ![]() .
Тоді
.
Тоді ![]() .
.
Оскільки ![]() ,
то
,
то ![]() . Тоді
. Тоді ![]() ,
тобто
,
тобто ![]() є лінійною комбінацією
є лінійною комбінацією ![]() і
і ![]() .
Отже вектори
.
Отже вектори ![]() лінійно залежні за першим означенням.
лінійно залежні за першим означенням.
Теорему доведено.
Теорема 4. Довільнічотиривектори геометричногопростору лінійно залежні.
Доведення.
Нехай маємо систему ![]() .
Якщо серед них є трійка компланарних,
то вони очевидно лінійно залежні. Нехай
такої трійки немає.
.
Якщо серед них є трійка компланарних,
то вони очевидно лінійно залежні. Нехай
такої трійки немає.
Візьмемо
точку А
і прикладемо до неї дані вектори.
Побудуємо паралеліпіпед, діагональ
якого є ![]() ,
а ребра знаходяться на прямих, що містять
вектори
,
а ребра знаходяться на прямих, що містять
вектори ![]() .
.

За означенням додавання
векторів маємо ![]() .
Оскільки
.
Оскільки ![]() ,маємо
,маємо ![]() .
.
Тоді
![]() ,
а тому
,
а тому ![]() – лінійно залежна.
– лінійно залежна.
Теорему доведено.
Зауваження.Мимохідь ми довели таке важливе твердження: будь-який вектор у просторі можна розкласти за трійкою некомпланарних векторів.
Поняття базису простору і площини
Означення. Максимальноюлінійно незалежною системою векторів простору (площини) називається така лінійно незалежна система векторів, приєднання до якої будь-якого вектору простору (площини) приводить до лінійно залежної системи.
Означення. Базисом називається упорядкована максимальна лінійнонезалежна система векторів простору(площини).
З попереднього випливає, що базисом площини є будь-яка упорядкована система двох неколінеарних векторів, а базисом простору – будь-яка упорядкована трійка некомпланарних векторів.
Теорема. Будь-який вектор площини(простору) можна розкласти і при тому єдиним чином за векторами базису.
Доведення.
Доведемо цю теорему в просторі.
Розглянемо
базисні вектори ![]() .Візьмемо довільний вектор
.Візьмемо довільний вектор
![]() .
.
Зауважимо, що можливість розкладання доведено у теоремі 4 про геометричний зміст лінійної залежності.
Тож
маємо ![]() .
.
Доведемо єдиність розкладання.
Припустимо
супротивне, що для ![]() має місце ще одне розкладання.
має місце ще одне розкладання.
![]() .
.
Зауважимо,
що оскільки розкладання відрізняються,
то різними є принаймні одна пара
коефіцієнтів ci,
di.
Припустимо (для визначеності), що ![]() .
.
Тоді
отримуємо: ![]()
![]()
Оскільки
![]() ,
то отримано рівність
,
то отримано рівність ![]() ,
що стверджує про лінійну залежність
векторів базису. Отримано суперечність
до означення базису.
,
що стверджує про лінійну залежність
векторів базису. Отримано суперечність
до означення базису.
Теорему доведено.
Означення. Координатами вектора у заданому базисі називаються коефіцієнти розкладання цього вектора за векторами базису.
