
- •Векторна алгебра
- •Системи лінійних алгебраїчних рівнянь. Метод послідовного виключення невідомих (метод Гаусса).
- •Поняття вектора, лінійні операції над векторами.
- •Поняття лінійно залежних і лінійно незалежних систем векторів.
- •Геометрична інтерпретація поняття лінійної залежності.
- •Поняття базису простору і площини
- •Афінна система координат.
- •Додатковий матеріал з векторної алгебри
- •Поняття лінійного простору.
- •Найпростіші властивості векторного простору.
- •Теорія визначників n-го порядку.
- •Перестановки з n символів.
- •Підстановки n-го степеня.
- •Поняття і властивості визначника n-го порядку
- •Мінори і алгебраїчні доповнення визначника
- •Лема до теореми Лапласа. Теорема Лапласа.
- •Застосування теорії визначників до лінійних систем алгебраїчних рівнянь. Теорема Крамера та лема до неї
- •Векторний простір
- •Подальше вивчення векторного простору.
- •Поняття рангу системи векторів.
- •Поняття рангу матриці. Теорема про ранг матриці.
- •Загальна теорія лінійно-алгебраїчних рівнянь
- •Критерій сумісності лінійних алгебраїчних рівнянь
- •Критерій визначеності і невизначеності системи
- •Однорідна система рівнянь. Фундаментальна система розв'язків однорідної системи рівнянь.
- •Зв’язок між розв’язком неоднорідної і відповідної однорідної системи рівнянь.
- •Алгебра матриць
- •Множиння матриць.
- •Матриці обернені до даних. Умови їх існування.
- •Операції додавання і множення на число.
- •Скалярні матриці.
- •Операції над прямокутними матрицями.
- •Псевдообернені матриці.
- •Комплесні числа.
- •Побудова множини комплексних чисел.
- •Полярна система координат.
- •Тригонометрична форма комплексного числа. Операції множення та ділення в тригонометричній формі.
- •Операції піднесення до степеня
- •Операція здобуття кореняn-ого степеня з комплексного числа
- •Кореніn-ого степеня з одниці
- •Комплексно-спряжені числа
- •Нерівність трикутника
- •Література
Матриці обернені до даних. Умови їх існування.
Внаслідок того, що множення матриць, взагалі кажучі, не комутативне, в цьому питанні слід розглядати ліві обернені матриці праві.
Означення. Матриця,
що умовно позначається
![]() , називається лівою оберненою до матриці
А, якщо вона задовольняє умову
, називається лівою оберненою до матриці
А, якщо вона задовольняє умову![]()
![]() .
.
Означення. Матриця,
що умовно позначається
![]() ,
називається правою оберненою до матриці
А, якщо вона задовольняє умову
,
називається правою оберненою до матриці
А, якщо вона задовольняє умову![]() .
.
Для з’ясування умов існування обернених матриць введемо поняття невироджених (неособливих) і вироджених (особливих) матриць.
Означення. Квадратна матриця називається невиродженою , якщо її визначник не дорівнює нулю. В противному разі квадратна матриця називається виродженою.
Теорема 1. Жодна вироджена матриця не має ні лівої оберненої, ні правої оберненої матриці.
Доведення.
Нехай задана матриця А, detA= 0. Треба
довести, що не існує ні правої оберненої,
ні лівої оберненої матриці. Припустимо,
що існує хоча б одна з них. Нехай існує
ліва обернена матриця. Тоді
![]() (з означення). Застосуємо теорему про
визначник добутку матриць:
(з означення). Застосуємо теорему про
визначник добутку матриць:
det E = det
![]() . det A ,
. det A ,
1 = 0, отримали суперечність.
Таким
чином, не існує
![]() , так само доводиться, що не існує
, так само доводиться, що не існує![]() .
.
Теорему доведено.
Теорема 2. Для будь-якої невиродженої матриці існує і ліва обернена, і права обернена, і вони рівні .
Доведення. Нехай задано матрицю А.
 ,
,
причому
detA=d
![]() 0
.
0
.
Треба
довести, що існує ліва обернена , права
обернена матриці, та
![]() =
=![]() . З матриці А побудуємо матрицю
. З матриці А побудуємо матрицю![]() ,
заміною кожного елементаaij
його алгебраїчним доповненнямАijі протранспонувавши отримаємо
матрицю:
,
заміною кожного елементаaij
його алгебраїчним доповненнямАijі протранспонувавши отримаємо
матрицю:
![]() =
=
![]()
 .
.
Доведемо,
що
![]() задовольняє дві умови:
задовольняє дві умови:
А
 = Е ;
= Е ; А = Е .
А = Е .
Доведемо
1) Застосувавши правило множення, лему до теореми Крамера і наслідок з теореми Лапласа маємо:
А
![]() =
=
 =
=
 =
=
 .
.
Так само, безпосереднім множенням матриць доводиться друга рівність.
З
першого пункта випливає
![]() =
=![]() , а з другого пункту
, а з другого пункту![]() =
=![]() .
.
![]() .
.
Отже ми довели існування оберненої матриці та її обчислення:
![]() =
=
![]()
 .
.
Вправа.
Довести єдиність
матриці
![]() (Доведення проводиться за схемою
доведення єдиності протилежного
вектора).
(Доведення проводиться за схемою
доведення єдиності протилежного
вектора).
Операції додавання і множення на число.
Означення. Сумою
матриць А і В , А=(![]() )
, В=(
)
, В=(![]() )
, називається матрицяD,
елементи якої обчислюються за законом
)
, називається матрицяD,
елементи якої обчислюються за законом
D= (![]() +
+![]() ).
).
Означення. Добутком матриці А на число k, називається матриця F, елементи якої обчислюються за законом
F= (k![]() ).
).
Введені операції мають такі властивості :
А + В = В + А ;
(А + В)+С = А+(В + С) ;
: А + = А + + А ;
=
 .
.
4) А (-А) : А + (-А) = (-А) + А = 0.
Вона
і снує , тому що є (-А) = (-![]() )
.
)
.
5) А = А ;
k (l A) = (k l) A ;
k (A + B) = kA + kB ;
(k + l) A = kA + lA :
Перевірити самостійно.
Таким
чином, множина всіх матриць є векторним
простором, більш того, арифметичним,
вимірності
![]() .
.
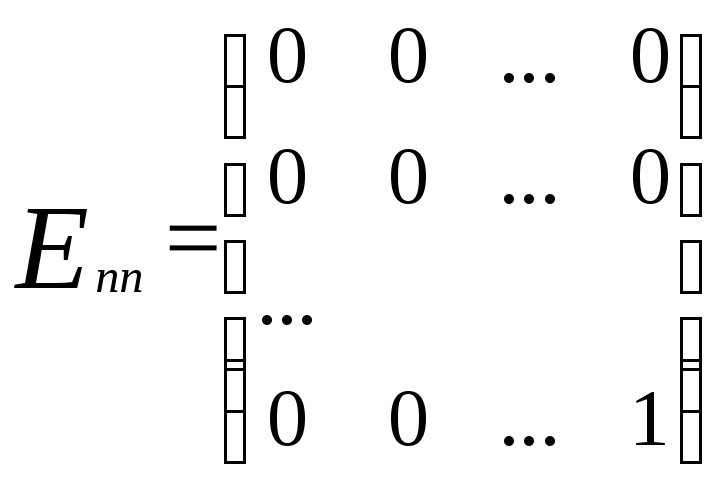
Розглянемо
хоча б один базіс цього простору. Це так
звані матриці
![]() .
.
![]() =
=
 .
.
Таких матриць існуєn2.
 ,
, , … ,
, … , ,
,
 ,
,  ,
… ,
,
… , 
Доведемо, що це базис. Доведемо, що це лінійно незалежні матриці. Для цього з’ясуємо, при яких kij виконується рівність
![]() (*)
(*)
 = 0 .
= 0 .
 ,
,
![]()
![]() .
.
Отже рівність (*) виконується лише в нульовому випадку усіх kij, тому матриці лінійно залежні.
З
того, що вимерність простору матриць
дорівнює
![]() ,
випливає, що матриці
,
випливає, що матриці![]() утворюють базіс. Тоді будь-яка матриця
А повинна бути лінійною комбінацією
матриць
утворюють базіс. Тоді будь-яка матриця
А повинна бути лінійною комбінацією
матриць![]() .
Знайдемо цю лінійну комбнацію.
.
Знайдемо цю лінійну комбнацію.
Розглянемо довільну матрицю А. Доведемо, що
А =
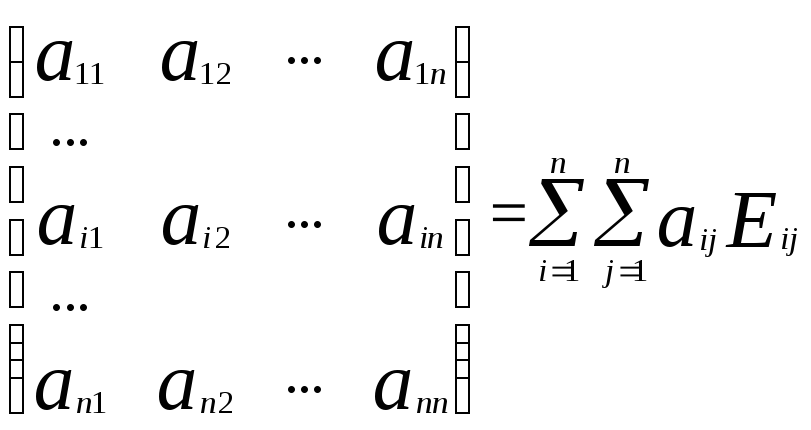 .
.
Введемо в розгляд допоміжну матрицю:
 .
.
Доведемо,
що цю матрицю можна подати у вигляді ![]() .
.
Насправді

Розглянемо тепер матрицю А. Її можна подати у вигляді

Застосуємо до кожного доданку попередню формулу
![]()
Вправа.Довести, що операція множення матриць і додавання матриць підпорядковується дистрибутивному закону :
А (В + С) = АВ + ВС .
Доведення.
Необхідність. Нехай
матриця С є скалярною. Треба довести,
що
![]() ,
А. З того, що матриця С скалярна, вона
має вигляд
,
А. З того, що матриця С скалярна, вона
має вигляд
С =

![]() .
.
Вище було доведено, що така матриця комутує з будь-якою матрицею А. Таким чином, необхідність доведена.
Достатність.Нехай деяка матриця С загального вигляду
С =
 ,
,
комутує
з будь-якою матрицею А . Треба довести,
що матриця С – скалярна матриця, тобто
![]() ,
,![]() , якщоi
j .
, якщоi
j .
З
того, що
![]() для будь-якої матриці А, випливає
для будь-якої матриці А, випливає![]() .
.

 (1)
(1)
 .
.
 (2)
(2)
Матриці (1), (2) за умовою теореми рівні, тому що на однакових місцях повинні знаходитись рівні елементи. Порівняємо елементи i-тих рядків ицх матриць.
0
=
![]() , 0 =
, 0 =![]() ,
… ,
,
… ,![]() ,
0 =
,
0 =![]()
![]() ,j =
1,2,…n.
,j =
1,2,…n.
Таким чином, ми одержали, що матриця С має діагональні елементи рівними, а елементи позадіагональні є нульовими, тобто матриця С – скалярна матриця.
