16. Матрица линейного преобразования. Связь между координатами вектора и его образа.
Пусть дано n–мерное действительное линейное пространство Vn. e1,e2,…en - базис этого пространства (е – базис, записанный в столбец). Всякое линейное преобразование пространства Vn однозначно определяется заданием образов e1,e2,…en всех векторов e1,e2,…en.
1.
…
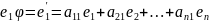
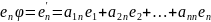
2.
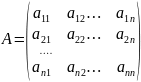
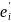-i-й
столбец
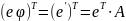
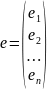
Связь между координатами вектора и его образами:
Пусть дано n–мерное действительное линейное пространство Vn. e1,e2,…en - базис этого пространства (е – базис, записанный в столбец), линейное преобразование и матрица А.
+
…
=>
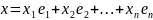
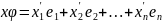
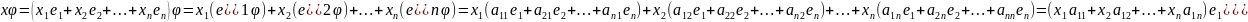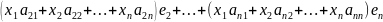
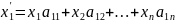
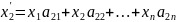
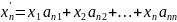
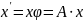
17. Матрица перехода от одного базиса линейного пространства к другому. Преобразование координат вектора при смене базиса.
Матрицей перехода от базиса e1,e2,…,en (1) к базису e’1,e’2,…,e’n (2) линейного пространства V называется квадратная матрица порядка n, в j-том столбце которой стоит столбец координат вектора e’j в базисе (1).
…
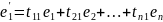
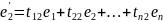
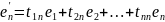
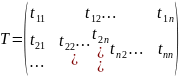
r(T)=n
detT≠0
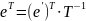
Преобразование координат вектора при изменении базиса:
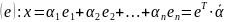
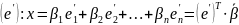
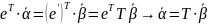
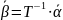
18. Связь между матрицами линейного преобразования в разных базисах. Подобные матрицы.
Рассмотрим пространство Vn: (e1,e2,…,en) - e и (e’1,e’2,…,e’n) — e'
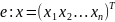
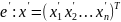
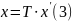
Пусть задано —линейное преобразование, А —его матрица в базисе е, В —его матрица в базисе е', T —матрица перехода от е к e'.
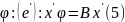
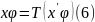
Помножим
(3) на А =>
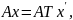с учетом (4)
.
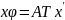С учетом (6) =>
,
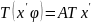а с учетом (5) =>
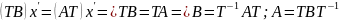
Oпред:
Если
для квадратных матриц А и В выполняется
условие
,
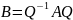где Q —некоторая невырожденная матрица,
то матрицы А и В называются подобными,
при этом говорят что матрица В получена
из А транспонированием матрицей Q.
Определители подобных матриц равны
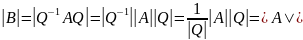
Теорема: Матрицы задающие одно и тоже линейное преобразование в разных базисах подобны между собой. При этом матрица линейного преобразования φ в базисе е' полученная транспонированием матрицей этого преобразования в базис е матрицей перехода от базиса е к базису е'.
19. Операции над линейными пространствами.
Пусть в пространстве Vn задано два лин. преобразования φ и ψ.
1) Суммой лин. преобразований φ и ψ
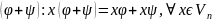
Сумма преобразований есть лин. преобразование.
Доказательство:
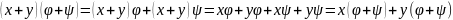
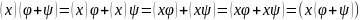
Если
преобразование
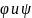задаются матрицами А и В , то преобразование
(φ
+ ψ)
задается матрицей С=А+В.
2) Произведение преобразований .
Произведение
преобразований – преобразование φψ,
определенное условием
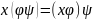
Преобразование φψ - линейное.
Докажем:
1. (х+у)φψ = ((х+у)φ)ψ = (хφ+уφ)ψ = (хφ)ψ+(уφ)ψ = х(φψ)+у(φψ).
2. (λх)φψ = ((λх)φ)ψ = (λ(хφ))ψ = λ((хφ)ψ) = λх(φψ).
Если φ и ψ определены матрицами А и В, то φψ определены С=А*В
3)Умножение преобразования на число
Произведением лин. преобразования φ на число λ – преобразование λφ, определяющееся условием:
1. х(λφ)= λ(хφ)
Преобразование λφ – линейное.
2. Если φ задается матрицей А, то λφ определяется λА.