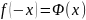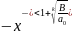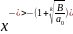- •16. Матрица линейного преобразования. Связь между координатами вектора и его образа.
- •17. Матрица перехода от одного базиса линейного пространства к другому. Преобразование координат вектора при смене базиса.
- •18. Связь между матрицами линейного преобразования в разных базисах. Подобные матрицы.
- •19. Операции над линейными пространствами.
- •20. Собственные значения и собственные векторы линейных преобразований. Порядок нахождения собственных векторов линейного пространства.
- •21. Определение эвклидового пространства. Примеры. Длина вектора и угол между векторами в эвклидовом пространстве.
- •22. Неравенство Коши-Буняковского в эвклидовом пространстве. Неравенство треугольника.
- •23. Ортогональность векторов. Процесс ортогонализации систем линейно независимых векторов. Ортонормированные базисы.
- •24. Ортогональные матрицы. Свойства ортогональных матриц.
- •26. Симметрические преобразования эвклидовых пространств.
- •27. Квадратические формы. Матрица квадратичной формы. Смена квадратичной формы при линейном преобразовании неизвестных.
- •29. Теорема о приведении симметричной матрицы к диагональному виду. Приведение квадратичной формы к главным осям.
- •31.Упрощение уравнений линий второго порядка на плоскости.
- •25. Ортогональные преобразования эвклидовых пространств.
- •28. Канонический вид квадратичной формы. Приведение квадратичной формы к каноническому виду методом Лагранжа. Закон инерции квадратичных форм.
- •2. Деление многочленов. Теорема о делении с остатком. Свойства делимости многочленов.
- •3. Наибольший общий делитель двух многочленов. Алгоритм Эвклида для нахождения наибольшего общего делителя
- •6. Понятие кратного корня многочлена. Производная многочлена. Связь между корнями многочлена и его производной.
- •7. Основная теорема алгебры и следствие из нее.
- •5. Корень многочлена. Теорема Безу. Схема Горнера деления многочлена на многочлен первой степени.
- •8. Рациональные корни многочлена с целыми коэффициентами.
- •9. Многочлены с действительными коэффициентами. Теорема про комплексные корни многочлена.
- •10. Границы действительных корней многочлена. Лемма о знаке старшего члена многочлена. Некоторые способы оценки корней многочленов.
- •15. Линейные преобразования линейных пространств. Примеры.
- •11. Система Штурма: определение и построение для заданного многочлена. Теорема Штурма. Локализация корней методом Штурма.
- •12. Приближенные методы вычисления корней многочленов. Метод половинного деления и метод Ньютона.
- •13. Определение линейного пространства. Примеры. Свойства линейного пространства.
- •14. Линейная зависимость и линейная независимость векторов. Размерность и базис линейного пространства.
5. Корень многочлена. Теорема Безу. Схема Горнера деления многочлена на многочлен первой степени.
Теорема
Безу.
Рассмотрим
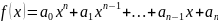 .
Если
.
Если
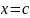 ,
то
,
то
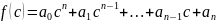 .
Число
.
Число
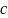 – корень многочлена, если
– корень многочлена, если
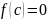 .
Значение многочлена
,
при
равно остатку от деления
на многочлен
.
Значение многочлена
,
при
равно остатку от деления
на многочлен
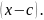
Доказательство:
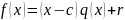 ;
;
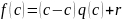 .
.
Следствие:
элемент
является корнем
,
когда
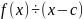
Схема Горнера.
f(x)=(x-c)q( r) +r
A0xn+A1xn-1+…+ A(n-1)x + An=(x-c)(Bo xn-1+B1xn-2+ …+ B(n-1))+r
Xn: A0=B0 B0=A0
Xn-1:A1=B1-c*B0 B1=B1+c*B0
…………
X1: A(n-1)=B(n-1)-c*B(n-2) B(n-1)= A(n-1)+ c*B(n-2)
X0: An=r r = An+c*B(n-1)
Многочлен S(x) называется делителем многочлена f(x) если существует Р(x) : f(x) = S(x)*P(x). Для любых многочленов f(x) и g(x) можно указать такие 2 многочлена Q(x) и R(x) что f(x) = g(x)*Q(x)+R(x), при этом Q(x) и R(x) определяются однозначно.
Доказательство.
Q1(x), R1(x) : f(x) = g(x)*Q1(x)+ R1(x)
R1(x)<Q1(x)
_q(x)-Q1(x)=R1(x)-r(x)
_q(x)=Q1(x) r(x)=R1(x) следовательно представление однозначно.
8. Рациональные корни многочлена с целыми коэффициентами.
Теорема.
Если целое число
является корнем многочлена с целыми
коэффициентами, то оно является делителем
свободного члена
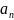 .
.
Доказательство.
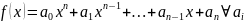 –
целые числа –корень
–
целые числа –корень
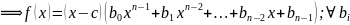 –целые числа;
–целые числа;
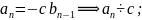
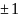 не является корнем
не является корнем
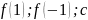 –целый корень
–целый корень
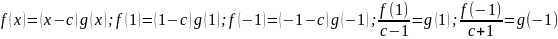 .
.
Порядок нахождения целых корней:
Выписать все делители
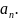
Для каждого делителя определяем выражение вида
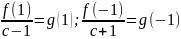 .
Если хотя бы одно из них не целое число,
то вычеркиваем из кандидатов.
.
Если хотя бы одно из них не целое число,
то вычеркиваем из кандидатов.Если оба выражения – целые числа, то подставляем делитель в многочлен.
Теорема
о рациональных корнях многочлена.
Если многочлен
имеет рациональный корень
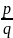 ,
то
,
то
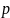 –
является делителем
,
a
–
является делителем
,
a
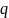 –
делителем старшего коэффициента
–
делителем старшего коэффициента
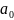 .
.
Доказательство.
Пусть
–
корень многочлена
.
Тогда
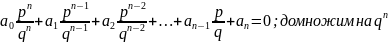 ;
;
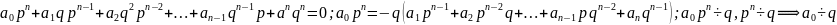
Следствие. Если многочлен с целыми коэффициентами, старший коэффициент которого равен единице, имеет рациональный корень, то этот корень – целое число
9. Многочлены с действительными коэффициентами. Теорема про комплексные корни многочлена.
Рассмотрим многочлен – действительные числа.
Теорема.
Комплексные корни многочлена входят
в него попарно сопряженные:
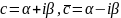
Лемма.
Если число
 получено в результате действий сложения,
вычитания, умножения, деления
получено в результате действий сложения,
вычитания, умножения, деления
 ,
то, заменив
на сопряженные, и проделав те же самые
операции, получим:
,
то, заменив
на сопряженные, и проделав те же самые
операции, получим:
 ;
;
 ;
;
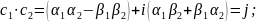
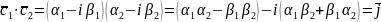
Доказательство теоремы: ; ;

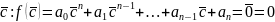
10. Границы действительных корней многочлена. Лемма о знаке старшего члена многочлена. Некоторые способы оценки корней многочленов.
Лемма.
При достаточно больших
 ,
а именно
,
а именно
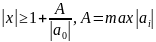 ,
знак многочлена
определяется
знаком старшего члена
,
знак многочлена
определяется
знаком старшего члена
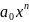 .
Все корни многочлена содержатся внутри
круга
.
Все корни многочлена содержатся внутри
круга
 ;
;
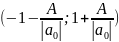
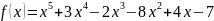
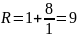
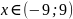
Оценка верхней границы положительных корней.
Рассмотрим многочлен
1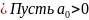
2)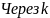 - обозначим номер первого отрицательного
коэффициента
- обозначим номер первого отрицательного
коэффициента

3)
Через
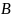 - обозначим
- обозначим
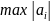 ,
где
,
где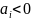 .
.
Тогда
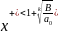 ;
;
Оценка нижней границы.