23. Ортогональность векторов. Процесс ортогонализации систем линейно независимых векторов. Ортонормированные базисы.

Ортогональными называются векторы, скалярное произведение которых равно нулю.

Система векторов а₁, а₂, …, а_k 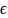E_k наз. ортогональной, если любые различные два вектора из них ортогональны, то есть их скалярное произведение равно нулю.

Всякая ортогональная система ненулевых векторов E_n линейно независима.

Теорема: Если а₁, а₂, …, а_k линейно независимая система векторов пространства E_n, то из нее некоторым способом можно построить ортогональную систему b₁, b₂, …, b_k ненулевых векторов этого же пространства. Этот процесс наз. ортогонализацией.

Базис e₁,e₂,…,e_n E_n наз. ортонормированным, если он ортогонален и все векторы его нормированы, то есть

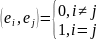
Теорема: Всякое евклидовое пространство обладает ортонормированными базисами.

24. Ортогональные матрицы. Свойства ортогональных матриц.

Матрица

наз. ортогональной, если соответствующая ей система векторов:

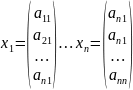- ортогональна.

При этом х₁,х₂,…,х_n E_n

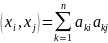
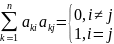
Теорема: Необходимое и достаточное условие ортогональной матрицы А является А^ТА=Е

Следствия:

1. Определитель ортогональной матрицы = 1

2. Невырожденная

3. Произведение ортогональных матриц = ортогональной матрице.

4. А^Т=А^-1

5. Если А – ортогональна, то А^Т – тоже ортогональна.

Свойства:

1. Столбцы и строки ортогональной матрицы образуют системы ортонормированных векторов.

2. Определитель ортогональной матрицы равен 1

3. Ортогональные матрицы соответствуют линейным операторам, переводящим ортонормированный базис линейного пространства в ортонормированный.

4. Множество ортогональных матриц порядка n над полем k образует группу по умножению, так называемую ортогональную группу, которая обозначается O(n, k).

26. Симметрические преобразования эвклидовых пространств.

А –симметрическая, если a_ij=a_ji

A^T=A

Линейное преобразование n-мерного евклидова пространства наз. симметрическим, если:

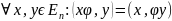(1)

Теорема 1: Симметрическое преобразование евклидова пространства в любой ортонормированной базе, задается симметрической матрицей.

Теорема 2: Все характеристические корни сим. преобразования действительны.

Теорема 3: Линейное преобразование  є Еn тогда и только тогда будет симметрическим, если в пространстве Еn существует ортонормированный базис, составленный из собственных векторов этого преобразования.

Теорема 4: Собственные векторы симметрического преобразования , относящиеся к различным собственным значениям, между собой ортогональны.

Доказательство:  - симметр. преобразование.

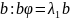
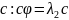
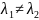
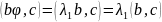
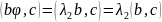
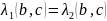
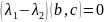
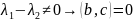
- ортогональны

27. Квадратические формы. Матрица квадратичной формы. Смена квадратичной формы при линейном преобразовании неизвестных.

Действительной квадратичной формой f от x1,x2,…,xn наз. сумма произведения пар этих неизвестных с действительных коэффициентов

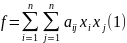
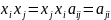
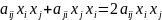
Матрицей квадратичной формы f, называется матрица составляющиеся из коэффициентов а_ij. Ее ранг - ранг квадратичной формы. Если ранг = n, матрица невырожденная, то и квадратичная форма называется невырожденной. Поскольку а_ij= а_ji, то матрица квадратичной формы – симметрическая.

f=x^TAx

Изменение квадратичной формы при линейном преобразовании неизвестных.

Выполним в (1) линейное преобразование:

x₁=q₁₁y₁+q₁₂y₂+…+q_1ny_n

x₂=q₂₁y₁+q₂₂y₂+…+q_2ny_n

. . . . . . . . . . . . . . . . . . . .

х_n=q_n1y₁+q_n2y₂+…+q_nny_n

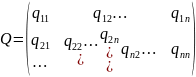
x=Qy

Теорема: Если в действительной квадратичной форме (1) от x₁,x₂,…,x_n с матриц А произвести линейные преобразования неизвестных с матрицы Q, то в результате получится другая квадратичная форма от новых неизвестных у₁, у₂,…,уn с матрицей B=Q^TAQ

Доказательство:

f= x^TFy x=Qy

x^T= (Qy)^T = y^TQ^T

f= y^T(Q^TAQ)y = y^TBy B=Q^TAQ

В=В^Т

B^T=(Q^TAQ)^T=Q^TA^TQ^T)^T=Q^TAQ=B

Следовательно В – симметричная матрица.