4. Операції піднесення до степеня

Поняття цілого степеня комплексного числа вводиться так само як і для дійсного числа. Нагадаємо, щопри.

Домовились вважати . Для введенняіснують два шляхи.

1. , де

2. 

Для корректності введеного поняття треба виконати вправу:

1. Довести

2. Довест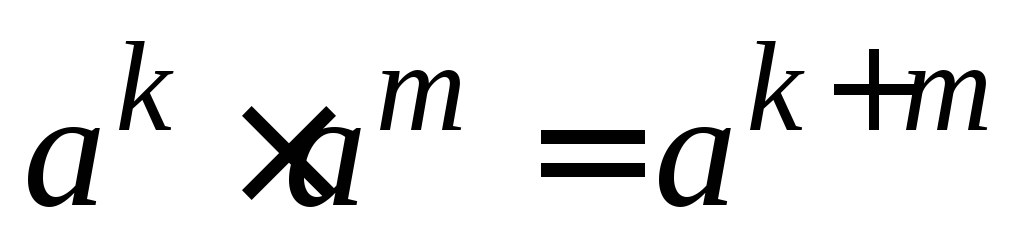и при.

1. Розглянемоспочатку операцію піднесення в алгебраїчній формі. Нехай задано число. Оскільки з попередніх означень випливає, що піднесення до цілого степеня зводиться до піднесення до натурального степеня, то можна скористатися формулою Бінома Ньютона:

Розглянемо таблицю множення числа і

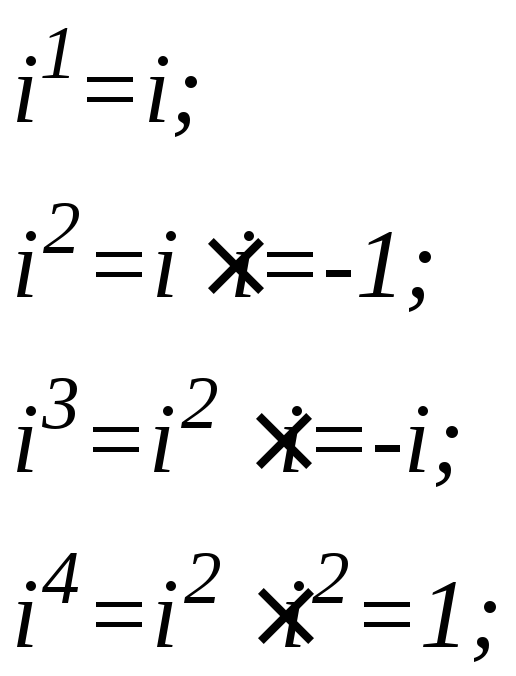з цього випливає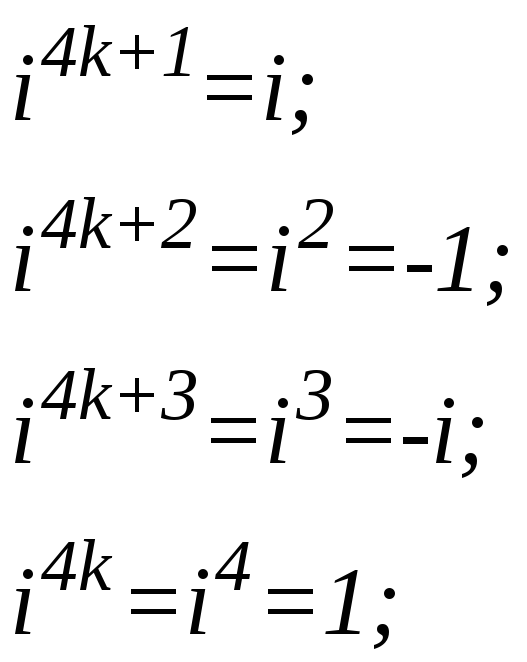

Використовуючи таблицю множення та виділяючи дійсну та уявну частину, отримаємо

(1)

2. Розглянемооперацію піднесення до степеню, колизадано в тригонометричній формі.

Використовуючи правило множення комплексних чисел в тригонометричній формі, маємо

.

Тобто, - формула Муавра

(2)

Застосуємо отримані рівності (1) і (2) для знаходження розкладання ічерезі. Окремі випадки цих формул приn=2,3 відомі зі шкільного курсу.

Застосуємо до числа формулу (2). В тригонометричній формі

(3)

Застосуємо формулу (1) при , отримаємо

Порівнюючи в формулах (3) і (4) дійсні та уявні частини, отримаємо

(4)

5. Операція здобуття кореняn-ого степеня з комплексного числа

Нехай задане комплексне число .

ОзначенняКоренемn-ого (n≥2) степеня з комплексного числаназивається комплексне числотаке, що

.

Нехай число задано в алгебраїчній формі. Шукатимемотакож в алгебраїчній формі.Розглянемо найпростіший випадок n=1. Тоді за попереднім означенням треба знайти дійсні числас і d такі що

Тобто,

Порівнюючи дійсні та уявні частини, отримаємо дійсну нелінійну систему рівнянь.

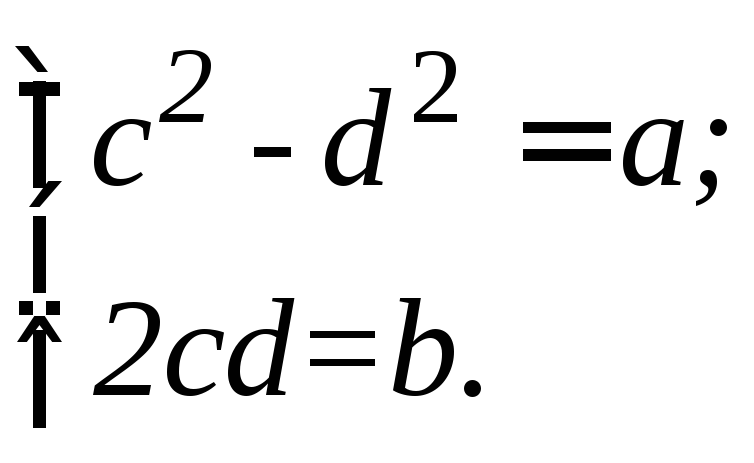
Більш складна система виникає, якщо таким шляхом вилучати корені степеня n≥3.

Розглянемо це питання для комплексного числа заданого в тригонометричній формі.

Шукатимемо також в тригонометричній формі.

За означенням, користуючись формулою Муавра, маємо

.

З цієї рівності випливає

Звідси випливає (арифметичний корінь),.

Отже

Насправді, щоб отримати всі корені достатньо змінювати . Нехай. Доведемо, щозбігатиметься з одним з коренів. Поділимокнаn:

.

Тоді

Скористаємося періодичністю тригонометричних функцій, тоді

Отже, отримали формули

ЗауваженняВ шкільному курсі символ вживався лише для арифметичних коренів. Тепер ми вживатимемоцей символ в більш широкому сенсі.

6. Кореніn-ого степеня з одниці

Застосуємо отриману формулу в окремому випадку при . Подамов тригонометричній формі:

Тоді,

Кореніn-ого степеня з 1 мають цікаві властивості.

Властивість 1Добуток двох коренівn-ого степеня з одиниці є також коренемn-ого степеня з одиниці.

Доведення. Нехайта- кореніn-ого степеня з одиниці, тобто. Треба довести, що, тобто що.

Розглянемо

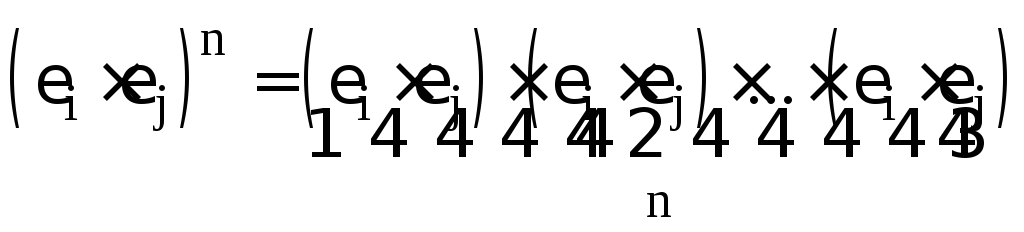
Внаслідок асоціативності і комутативності множення комплексних чисел маємо

що і треба було довести.

З цієї властивості випливає наслідок.

Наслідок 1.Будь-який натуральний степінь кореняn-ого степеня з одиниці є також коренемn-ого степеня з одиниці.

Властивість 2Число обернене до кореня n-ого степеня з одиницієтакож коренем n-ого степеня з одиниці.

Доведення. Нехай,- число обернене до, тому. Треба довести, що, тобто.

Розглянемо . Звідсивнаслідок коммутативності і ассоциативності множення маємо. Оскільки, то, що і треба було довести.

Наслідок 2.Будь-який від`ємний степінь кореня n-ого степеня з одиниці є також коренем n-ого степеня з одиниці.

Це випливає з того, що .

Оскільки , то з наслідків 1 та 2 випливає: будь-який цілий степінь кореня n-ого степеня з одиниці також є коренем n-ого степеня з одиниці.

В подальшому ці властивості в розділі теорії груп дозволять побудувати мультиплікативну групу коренів n-ого степеня з одиниці.

Розглянемо властивість, важливу з практичної точки зору.

Властивість 3.Добуток кореня n-ого степеня з числана корінь n-ого степеня з одиниці є коренем n-ого степеня з числа.

Доведення.Нехай. Треба довести, що, тобто що.

Розглянемо , що і треба було довести.

З цієї властивості випливає, що всі корені n-ого степеня з числа можна отримати помноживши одного з них на кожний корінь n-ого степеня з одиниці.