
- •Векторна алгебра
- •Системи лінійних алгебраїчних рівнянь. Метод послідовного виключення невідомих (метод Гаусса).
- •Поняття вектора, лінійні операції над векторами.
- •Поняття лінійно залежних і лінійно незалежних систем векторів.
- •Геометрична інтерпретація поняття лінійної залежності.
- •Поняття базису простору і площини
- •Афінна система координат.
- •Додатковий матеріал з векторної алгебри
- •Поняття лінійного простору.
- •Найпростіші властивості векторного простору.
- •Теорія визначників n-го порядку.
- •Перестановки з n символів.
- •Підстановки n-го степеня.
- •Поняття і властивості визначника n-го порядку
- •Мінори і алгебраїчні доповнення визначника
- •Лема до теореми Лапласа. Теорема Лапласа.
- •Застосування теорії визначників до лінійних систем алгебраїчних рівнянь. Теорема Крамера та лема до неї
- •Векторний простір
- •Подальше вивчення векторного простору.
- •Поняття рангу системи векторів.
- •Поняття рангу матриці. Теорема про ранг матриці.
- •Загальна теорія лінійно-алгебраїчних рівнянь
- •Критерій сумісності лінійних алгебраїчних рівнянь
- •Критерій визначеності і невизначеності системи
- •Однорідна система рівнянь. Фундаментальна система розв'язків однорідної системи рівнянь.
- •Зв’язок між розв’язком неоднорідної і відповідної однорідної системи рівнянь.
- •Алгебра матриць
- •Множиння матриць.
- •Матриці обернені до даних. Умови їх існування.
- •Операції додавання і множення на число.
- •Скалярні матриці.
- •Операції над прямокутними матрицями.
- •Псевдообернені матриці.
- •Комплесні числа.
- •Побудова множини комплексних чисел.
- •Полярна система координат.
- •Тригонометрична форма комплексного числа. Операції множення та ділення в тригонометричній формі.
- •Операції піднесення до степеня
- •Операція здобуття кореняn-ого степеня з комплексного числа
- •Кореніn-ого степеня з одниці
- •Комплексно-спряжені числа
- •Нерівність трикутника
- •Література
Поняття вектора, лінійні операції над векторами.
Розглянемо в просторі (на площині) множину всіх направлених відрізків. В цій множині можна по-різному ввести означення рівності напрямленнях відрізків і отримати три поняття вектора.
Означення 1. Два напрямлених відрізки називаються рівними, якщо:
вони колінеарні (знаходяться на одній або паралельних прямих);
мають однаковий напрямок;
мають однакові довжини.
Означення 2. Вільним вектором називається множина всіх рівних між собою в сенсі означення 1 напрямлених відрізків.
Введемо іншим чином означення рівності.
Означення 1'. Два напрямлених відрізки називаються рівними, якщо:
вони колінеарні;
мають однаковий напрямок;
знаходяться на одній прямій;
мають однакові довжини.
Означення 2'. Ковзним вектором називається множина всіх рівних між собоюусенсі означення1'напрямлених відрізків.
Означення 1''.Два напрямлених відрізки називаються рівними, якщо :
в них рівні довжини;
знаходяться на одній прямій;
однаково направлені і мають спільний початок.
Означення 2''. Зв'язаним вектором називається множина рівних між собою в сенсі означення 1'' напрямлених відрізків.
З останнього означення випливає, що зв'язаний вектор дорівнює лише собі. В даному курсі розглядатимемо лише вільні вектори.
Над векторами вводяться дві основні лінійні операції :
додавання векторів;
множення векторана число.
Означення 3. Сумою
двох векторів![]() і
і ![]() ,
називається вектор, що умовно позначається
,
називається вектор, що умовно позначається![]() ,
початок якого знаходиться в початку
вектора
,
початок якого знаходиться в початку
вектора![]() ,
кінець – у кінці вектора
,
кінець – у кінці вектора![]() ,
за умови, що початок вектора
,
за умови, що початок вектора![]() знаходиться в кінці вектора
знаходиться в кінці вектора![]() .
.
Означення 4. Добутком
вектора а на число к називається вектор,
що умовно позначається ![]() і має такі властивості:
і має такі властивості:
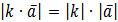
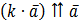 ,
якщо
,
якщо 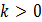 ,
і
,
і 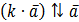 ,
якщо
,
якщо 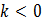
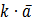 не має певного напрямку,
якщо
не має певного напрямку,
якщо 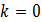 .
.
Властивості лінійних операцій (довести самостійно).
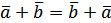 –комутативність
додавання.
–комутативність
додавання.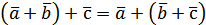 –асоціативність
додавання.
–асоціативність
додавання.Існує так званий нульовий вектор
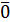 ,
тобто такий, для якого
,
тобто такий, для якого
![]() для довільного вектора
для довільного вектора
![]() .
.
Зрозуміло, що початок і кінець нульового вектора збігаються, тобто він має нульову довжину, а напрямок цього вектора невизначений.
Для будь-якого вектора
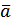 існує так званий протилежний вектор
існує так званий протилежний вектор
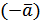 ,
тобто такий, що
,
тобто такий, що 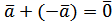 .
.
Вектори
![]() та
та ![]() мають протилежні напрямки та однакові
довжини.
мають протилежні напрямки та однакові
довжини.
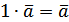 для довільного вектора
для довільного вектора
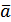 .
.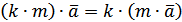 –асоціативність множення
на число.
–асоціативність множення
на число.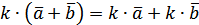 – дистрибутивність.
– дистрибутивність.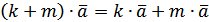 – дистрибутивність.
– дистрибутивність.
Поняття лінійно залежних і лінійно незалежних систем векторів.
Означення. Лінійною комбінацією
векторів![]() називається вектор
називається вектор![]() деpi- будь-які числа.
деpi- будь-які числа.
Означення 1. Система
векторів ![]() називається лінійно залежною, якщо
принаймні один з векторів цієї системи
є лінійною комбінацією інших.
називається лінійно залежною, якщо
принаймні один з векторів цієї системи
є лінійною комбінацією інших.
Інакше кажучи, ![]() .
.
Означення 2. Система
векторів ![]() називається лінійно залежною, якщо
існують числа
називається лінійно залежною, якщо
існують числа ![]() ,
серед яких принаймні одне
,
серед яких принаймні одне ![]() ,
що виконується рівність:
,
що виконується рівність:
![]()
![]() .
.
Теорема. При
![]() перше і друге означення лінійнозалежної системи еквівалентні.
перше і друге означення лінійнозалежної системи еквівалентні.
Доведення.
Нехай система векторів лінійно залежна за означенням 1.Треба довести, що вона лінійно залежна у сенсі означення 2.
Скористаємось означенням 1. Тоді виконується (1):
![]() .
.
Додамо
до обох частин даної рівності вектор
протилежний до ![]() :
:
![]()
Внаслідок комутативності і означення нульового вектора маємо:
![]()
Тобто
![]() ,
що виконується і рівність
,
що виконується і рівність ![]() ісистема лінійно залежна
за означенням 2.
ісистема лінійно залежна
за означенням 2.
Нехай тепер система векторів лінійно залежна за означенням 2:
![]() (
(![]() ).
).
Треба довести, що ![]() .
.
Додамо вектор ![]() до лівої та правої частини даної рівності:
до лівої та правої частини даної рівності:
![]()
Відомо,
що ![]() ,
тоді помноживши обидві частини рівності
на
,
тоді помноживши обидві частини рівності
на ![]() маємо:
маємо:
![]()
Тобто система є лінійно залежною за означенням 1.
Теорему доведено.
Зауваження. При
![]() ,
означення 1 лінійної залежності втрачає
сенс, тоді як за означенням 2
рівність
,
означення 1 лінійної залежності втрачає
сенс, тоді як за означенням 2
рівність ![]() при
при ![]() стає
стає![]() ,
тобто
,
тобто ![]() .
Маємо, що система з одного вектора
лінійно залежна тоді і тільки тоді, коли
цей вектор нульовий.
.
Маємо, що система з одного вектора
лінійно залежна тоді і тільки тоді, коли
цей вектор нульовий.
Теорема. Якщоусистемі векторів є лінійно залежна підсистема, то і вся система лінійно залежна.
Доведення.
Нехай
задана система ![]() .
Візьмемо її підсистему. Не зменшуючи
загальності міркувань вважатимемо, що
підсистема
.
Візьмемо її підсистему. Не зменшуючи
загальності міркувань вважатимемо, що
підсистема ![]() – лінійно залежна. Тоді
– лінійно залежна. Тоді ![]() :
:![]() .
.
Запишемо рівність в такому виді:
![]()
Тоді![]() такі, що
такі, що ![]() .
.
Система лінійно залежна за означенням 2.
Теорему доведено.
Означення. Система
векторів ![]() називається лінійно незалежною, якщо
рівність
називається лінійно незалежною, якщо
рівність ![]() виконується тоді і тільки тоді, коли
виконується тоді і тільки тоді, коли
![]() .
.
З вище доведеної теореми випливає, що якщо система лінійно незалежна, то всі її підсистеми також лінійно незалежні.
