
- •1.2 Акустические волны в скалярных средах
- •1.3 Интенсивность ультразвукового излучения
- •1.4 Биологическое действие ультразвука
- •1.5 Сферические волны
- •Функция Грина и формулы Кирхгофа
- •2.4 Поле сферического фокусирующего преобразователя
- •3.2 Уравнение Вестервельта и волны комбинационных частот
- •3.2. Коэффициент нелинейности биологических сред
- •Таблица 3.2
- •4. ГИДРОДИНАМИЧЕСКИЕ МЕТОДЫ
- •4.1 Уравнения течения вязкой несжимаемой жидкости
- •4.2 Элементы гемодинамики
- •4.3 Аппарат искусственного кровообращения
- •4.4 Вискозиметрия
- •4.5 Измерение артериального давления крови
- •5.1 Методы ультрацентрифугирования
- •5.2 Метод скорости седиментации
- •5.1. Электрические свойства биотканей
- •5.2. Источник внеклеточного поля
- •5.3 Воздействие постоянными и переменными токами и полями
- •5.4 Механизмы поглощения высокочастотных полей
- •Спектр ЭМИ
- •Вопросы для самостоятельного изучения
- •Литература
- •Излучение
- •Ионизирующее
- •6. ПОГЛОЩЕНИЕ ЭМИ
- •6.1 Поглощение СВЧ волн в биологических тканях
- •6.2 Обратные переходы и процессы релаксации
- •6.3 Флуктуационно-диссипационная теорема
- •6.4 Индуктотермия
- •6.5 Биологическое действие высокочастотного ЭМИ
- •Вопросы для самостоятельного изучения
- •Литература
- •7.1 История развития метода
- •7.2 Условие резонанса
- •7.3 Кинетика переходов
- •7.4 Уравнение Блоха
- •7.5 Спектр ЯМР
- •Квадратурное детектирование ЯМР сигналов
- •Чувствительность cw-ЯМР
- •РЧ импульсы и импульсная ЯМР-спектроскопия
- •Чувствительность импульсного ЯМР
- •Применение ЯМР-спектроскопии в биохимии
- •Зависящие от времени процессы в ЯМР
- •Химический анализ
- •Тип движения
- •Область значений частоты, Гц
- •Вибрационные и торсионные движения
- •Латеральная диффузия в мембранах
- •Диффузия в растворах
- •Вращательная диффузия в растворах
- •Конформационные изменения протеинов
1.ФИЗИЧЕСКИЕ ОСНОВЫ УЗИ
1.1Приборы и аппараты в медицине
Современная медицина базируется на широком использовании разнообразной аппаратуры, которая в подавляющем большинстве случаев является физической по методу измерения и измеряемым величинам. Понимание физических принципов, используемых для работы большей части современных устройств медицинского назначения, требует достаточно глубокого знания ряда специальных физических дисциплин. В одном курсе невозможно рассмотреть физические принципы устройства медицинской аппаратуры всех типов и различного клинического назначения, поэтому здесь наибольшее внимание будет уделено тем физическим методам, которые используют наиболее современные физические и технические достижения и в то же время не нашли своего отражения в других учебных курсах по медицинской физике. В соответствии с этим изложение коснется преимущественно физических основ эластографии, методов ультразвуковой медицинской диагностики, электрографии и методов магнито-резонансной томографии.
В то же время целесообразно сразу дать самые общие сведения о конструкции медицинской аппаратуры и применяемой в ней электронике. Являясь технической наукой, электроника основывается прежде всего на достижениях физики. В частности, выделяют физическую электронику, имея в виду раздел физики, рассматривающий электропроводимость тел, контактные и термоэлектронные явления и т.д.; под технической электроникой понимают те ее разделы, в которых описывается устройство приборов и аппаратов и схемы их включения; полупроводниковой электроникой называют все то, что относится к применению полупроводниковых приборов, и т.д..
Важно понимать, что медицина, как область применения электроники, использует ту же элементную базу и принципы конструирования аппаратов и систем, что и все другие области ее применения. Электронику можно разделить на три крупных раздела: вакуумная электроника, которая касается создания и применения электровакуумных приборов (электронные лампы, фотоэлектронные устройства, рентгеновские трубки, газоразрядные приборы); твердотельная электроника, которая охватывает вопросы создания и применения полупроводниковых приборов, в том числе и интегральных микросхем; квантовая электроника – специфический раздел электроники, имеющий отношение к лазерам и мазерам. С точки зрения конструирования разнообразные области применения электроники отличаются только полнотой использования указанных разделов. В частности, в настоящее время многие традиционно «неэлектрические» характеристики – температура, смещение тела, биохимические показатели и другие – стремятся при измерениях преобразовывать в электрические сигналы. Информацию, представленную электрическими сигналами, удобно регистрировать, сохранять и передавать на
большие расстояния.
Можно выделить следующие основные группы электронных приборов и аппаратов, используемых для медико-биологических целей. Во-первых, это аппараты, обеспечивающие дозирующее воздействие на организм различных физических факторов (ультразвук, электрический ток, электромагнитные поля и др.) с целью лечения. К ним относятся, в частности, аппараты микроволновой терапии, аппараты для электро- и лазерной хирургии, кардиостимуляторы, различные источники излучений и др. С физической точки зрения эти устройства являются генераторами различных полей и электрических сигналов.
Во-вторых – это аппараты для получения (съема) и регистрации медикобиологической информации. Такая информация может быть не только о процессах, происходящих в организме (биологические ткани, органы, системы), но и о состоянии окружающей среды (санитарно-гигиеническое назначение), о процессах, происходящих в протезах, и т.д. Сюда относится большая часть диагностической аппаратуры: ультразвуковые, рентгеновские и ЯМРтомографы, баллистокардиографы, фонокардиографы, реографы и др.. Для подавляющего большинства этих приборов в радиотехническом отношении характерно наличие усилителей электрических сигналов, аналого-цифровых преобразователей (АЦП), фильтров – аналоговых и цифровых, сигнальных процессоров и контроллеров, блоков памяти и т.д.. К этой группе можно отнести и относительно простую электромедицинскую аппаратуру для лабораторных исследований, например рН-метры.
Третью группу устройств составляют устройства передачи (телеметрии), обработки и хранения медико-биологической информации. В частности, для хранения и отображения информации в подавляющем большинстве современной диагностической аппаратуры используется встроенный или внешний компьютер. Первичная обработка и преобразование полученных данных (аналоговая фильтрация, аналого-цифровое преобразование и цифровая обработка зарегистрированной медико-биологической информации) может производиться, как отмечалось выше, соответствующими устройствами непосредственно в аппарате съема информации. В данном случае речь идет об устройствах, обеспечивающих передачу информации, и об устройствах, осуществляющих после ввода информации ее отображение, обработку математическими методами с последующим анализом, постановкой диагноза и созданием баз данных для хранения. Такого рода устройства в своей совокупности получили название телемедицинских систем, интенсивно развивающихся в последнее десятилетие. Отличительной особенностью таких систем является непременное использование встроенных и внешних компьютеров, компьютерных сетей и необходимого для этих целей программно-математического обеспечения. Иными словами, по сути речь идет о современных компьютерных технологиях в их чистом виде.
Применение электронных медицинских приборов и аппаратов повышает эффективность диагностики, оперативность и результативность лечения, расширяет их возможности, что в конечном итоге приводит к увеличению производительности труда медперсонала и сокращению времени лечения.

1.2 Акустические волны в скалярных средах
Наиболее полное описание многих явлений, принципиально важных для медицинских приложений ультразвука и акустической томографии, возможно только в рамках общей теории упругих сплошных сред. Такое описание способно полностью учесть вязкоупругие свойства биологических объектов и все виды упругих волн в них. Для медицинской УЗИ и акустической томографии наиболее важное значение имеет распространение ультразвуковых волн в неоднородных средах, а его рассмотрение является наиболее простым и наглядным при использовании гидродинамического подхода. Применимость гидродинамического подхода для акустики мягких тканей вытекает из малости модуля сдвига тканей, в результате чего ультразвук распространяется практически так же, как в жидкостях.
Рассмотрим вначале уравнения гидродинамики в однородной жидкой среде. Математически при гидродинамическом изучении движения жидкости ее состояние описывается с помощью функций, определяющих распределение скорости жидкости v(r,t) и каких-либо двух ее термодинамических величин,
например давления P(r,t) и плотности ρ(r,t). Иными словами, в
гидродинамике следят не за движением отдельных элементов объема жидкости, а за изменениями поля скоростей, давлений и плотности в каждой фиксированной точке пространства. В этом случае полное изменение скорости выделенного элемента объема жидкости включает в себя изменение, связанное с неоднородностью потока жидкости, т.е. с зависимостью скорости от точки наблюдения в пространстве. В таких эйлеровых координатах уравнение движения элемента объема жидкости с учетом сил вязкого трения имеет вид
∂v |
|
|
|
|
η |
|
(1.1) |
|
ρ |
∂t |
+ (v )v |
= − P +η∆v + (ς + |
3 |
)grad divv , |
|||
|
|
|
|
|
|
|
||
где η- динамическая сдвиговая вязкость и ς - объемная или вторая вязкость
жидкости. Уравнение (1.1) называется уравнением Навье-Стокса, которое без учета вязкости жидкости переходит в уравнение Эйлера. Второе слагаемое в квадратных скобках левой части носит название конвективной производной.
Второе уравнение – это обычное уравнение непрерывности
∂ρ |
|
|
, |
(1.2) |
|
+ (ρv) = 0 |
|||
∂t |
||||
которое получается из закона сохранения вещества в любом выделенном объеме:
∂ ∫ρdV = −∫ρvds . |
|
∂t V |
S |
Наконец, нужно учесть уравнение термодинамического равновесия, определяющее связь между мгновенными значениями плотности среды и давлением. Если считать неизменной энтропию каждого элемента объема жидкости, то полное изменение во времени давления, связанного с движением этого элемента, имеет вид
∂P |
|
∂P |
|
∂ρ |
= c 2 ∂ρ . |
(1.3) |
|
= |
|
||||||
∂t |
|
∂ρ |
|
∂t |
0 |
∂t |
|
|
S |
|
|
||||
Рассмотрим теперь среду без диссипации энергии и будем полагать, что распространяющаяся волна приводит к небольшим возмущениям плотности и давления на равновесном фоне: ρ = ρ0 + ρA , P = P0 + PA . Тогда и колебательные
скорости движения в каждой точке можно считать малыми. С учетом только линейных членов по малым ρA , PA и v из (1.1) и (1.2) получаем
ρ |
|
∂v |
|
(1.4) |
|
|
= − P , |
||||
|
0 |
∂t |
A |
|
|
∂ρA |
|
|
|
||
+ ρ0 v = 0 . |
(1.5) |
||||
|
|||||
∂t |
|
|
|
|
|
Если теперь применить операцию к первому уравнению, взять производную по времени от второго и учесть (1.3), то получим
|
ρ |
|
|
∂v |
= −∆P , |
(1.6) |
||||
|
|
|
∂t |
|||||||
|
|
0 |
|
|
|
|
A |
|
||
|
|
∂v |
|
1 |
∂2 P |
|
||||
ρ |
|
|
|
|
= − |
|
A . |
(1.7) |
||
|
∂t |
c 2 |
||||||||
0 |
|
|
|
|
|
∂t2 |
|
|||
|
|
|
|
|
|
|
|
0 |
|
|
Вычитая эти уравнения, получим волновое уравнение для изменения |
||||||||||
акустического давления |
|
|
|
|
1 |
|
∂2 P |
|
|
|
∆P |
− |
|
|
= 0. |
(1.8) |
|||||
|
|
|
|
A |
||||||
c 2 |
|
|||||||||
|
A |
|
|
∂t2 |
|
|
||||
|
|
|
|
|
0 |
|
|
|
|
|
Достаточно просто убедиться с помощью уравнений (1.3) – (1.5), что такой же вид будут иметь волновые уравнения для возмущений плотности и колебательной скорости.
1.3 Интенсивность ультразвукового излучения
Как известно, плотность потока энергии в любом волновом процессе описывается вектором Умова-Пойнтинга. Для звуковых волн эта величина
определяется как I = Pv , |
где P - акустическое давление. Интенсивность |
||
звукового излучения или |
акустическая интенсивность I = |
I |
показывает |
|
|
|
|
количество энергии, переносимой ультразвуковым излучением через единичную площадку за единицу времени. Для плоской бегущей волны, а также для участков волнового фронта, небольших по сравнению с его радиусом кривизны, можно воспользоваться следующим соотношением между
акустическим давлением и колебательной скоростью: P / ρ0 2c0 = v. Тогда
мгновенное значение интенсивности ультразвукового излучения в точке пространства с координатой r описывается выражением
|
1 |
|
|
2 |
|
|
|
I(r;t) = |
|
|
P |
|
(r;t), |
(1.9) |
|
ρ |
c |
|
|||||
|
0 |
|
0 |
|
|
|
|
где радиус-вектор положения точки наблюдения часто удобно выбирать в

цилиндрических координатах r = (z,r,ϕ) с учетом аксиальной симметрии
большинства фокусирующих ультразвуковых преобразователей. Для прямоугольной излучающей апертуры на больших расстояниях от нее также достаточно удобно пользоваться этими координатами.
Физически справедливость формулы (1.9) вытекает из следующих соображений. Несложно записать кинетическую энергию единицы объема скалярной среды, в которой распространяется звуковая волна. Для этого достаточно в обычном выражении для кинетической энергии заменить массу
тела на плотность среды: εK = ρ0 v2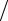 2 . Для нахождения потенциальной энергии
2 . Для нахождения потенциальной энергии
единицы объема среды следует учесть, что энергия любой упругой деформации по определению равна той работе, которую нужно совершить, чтобы изменить объем на величину dV . Такая работа, отнесенная к самой величине объема, с учетом только квадратичных членов по малым акустическим добавкам к плотности и скорости звука равна:
dA = −P dV |
= P dρ = |
P |
|
∂P |
|
−1 |
P |
|
||
|
|
dP = |
dP . |
|||||||
|
|
2 |
||||||||
V |
V |
ρ ρ |
|
∂ρ |
|
|
|
|||
|
|
|
ρ0c0 |
|
||||||
Интегрирование этого выражения |
приводит |
|
|
к простому |
выражению |
||||||||||
ε |
П |
= P2 2ρ c 2 |
. В результате полная энергия единицы объема скалярной среды, |
||||||||||||
|
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
участвующей в процессе распространения звука, описывается выражением |
|||||||||||||||
|
|
|
ε =ε |
K |
+ε |
П |
= ρ |
v2 |
+ |
P2 |
|
|
. |
(1.10) |
|
|
|
|
2 |
2ρ |
c |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
С другой стороны, непосредственно из уравнений гидродинамики (1.1) – (1.3) можно получить дифференциальное уравнение
∂ |
|
v2 |
|
|
P2 |
|
|
|
|
|
|
|
ρ |
|
+ |
|
|
|
+ div(Pv) = 0 |
, |
(1.11) |
|
|
|
2 |
|||||||
∂t |
|
2 |
|
2 |
ρ0c0 |
|
|
|
|
|
которое по форме выражает собой некоторый закон сохранения в дифференциальной форме. В данном случае это закон сохранения звуковой энергии.
Действительно, если полную энергию объема V обозначить через E , то
E = ∫V εdV
и
∂E |
= −∫Ids |
= −∫divIdV . |
(1.12) |
∂t |
S |
V |
|
Это интегральная форма закона сохранения энергии, из которой вместе с (1.11)
следует, что I = Pv .
Интенсивность акустического излучения является определяющей для многих физически интересных и практически важных явлений. Одним из них являются так называемые акустические течения в жидкостях, включая биологические жидкости. Если в выражении (1.12) под объемом

интегрирования понимать достаточно большой объем, вне которого акустического излучения уже нет (например, в результате поглощения волн), то интеграл по поверхности обращается в ноль. Следовательно, полная акустическая энергия во всем объеме распространения волн сохраняется, а ее убыль в результате диссипации энергии компенсируется притоком акустической энергии от ультразвукового преобразователя.
Распространение акустической волны, занимающей в пространстве конечную область (пространственный волновой пакет), приводит к переносу вещества, т.е. к движению жидкости. Действительно, импульс единицы объема жидкости можно определить в соответствии с выражением q = (ρ0 + ρ)v .
Подставляя сюда ρ = P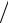 c02 , получаем
c02 , получаем
q = ρ0v + I . c0
При интегрировании этого выражения по объему первое слагаемое вклада в интеграл не дает, поскольку для потенциального движения скалярной жидкости
v = − ϕ . Тогда объемный интеграл снова можно преобразовать в поверхностный от потенциала ϕ , который равен нулю вне области
распространения волны. В результате полный импульс, связанный с движением жидкости, описывается выражением
|
1 |
|
∫V qdV = |
|
∫V IdV . |
c 2 |
||
|
0 |
|
Вид и характер акустического течения зависит от геометрии звукового поля, создаваемого ультразвуковым преобразователем, а его скорость значительно меньше колебательной скорости v , поскольку сам эффект представляет собой эффект второго порядка малости по v .
1.4 Биологическое действие ультразвука
Интенсивность ультразвукового излучения является главным параметром, способным описать потенциальный риск возникновения биологических эффектов при прохождении ультразвука. Кроме интенсивности к числу таких параметров относятся термический индекс (thermal index – TI), механический индекс (mechanical index – MI), выход акустической энергии (the acoustic power output) и максимальное отрицательное давление.
По международным стандартам механический индекс MI дается выражением
MI = k P−f
где P− - пиковое отрицательное давления в МПа, k =1МПа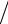

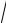 кГц – размерный
кГц – размерный
коэффициент. Термический индекс представляет собой отношение акустической мощности в данной точке ткани к такой акустическая мощности, которая вызывает при тех же условиях локальное повышение температуры в
тканях на 1 C . Эти параметры не указывают однозначно на возникновения негативных биоэффектов прохождения ультразвука, но могут служить, как описано ниже, для оценки потенциального риска их возникновения. Широкое применение ультразвуковых методов в диагностике обусловлено, в частности, его толерантностью. Тем не менее, ультразвуковое зондирование следует применять осторожно, с минимальным временем экспонирования и малыми уровнями акустической интенсивности.
Биологические эффекты, возникающие при акустических мощностях, превышающих диагностические уровни, хорошо известны. Эти эффекты широко используются в терапии. Повышение качества ультразвуковой диагностической аппаратуры иногда достигается за счет увеличения выходной мощности, которое сопровождается ростом пиковых значений интенсивности, поэтому необходимо иметь представление о возникающих биологических эффектах и физических механизмах, отвечающих за их возникновение. Анализ вопроса о связи между дозой облучения и результирующим биоэффектом усложняется, как правило, тем, что при разных условиях преобладают разные механизмы.
Тепловые механизмы проявляются, когда поглощение акустической энергии приводит к росту температуры среды (≈1ºС). Основной вклад в поглощение дают здесь такие механизмы диссипативных потерь, как молекулярная релаксация и внутреннее трение. Косвенный, но весьма заметный вклад в поглощение вносят нелинейные механизмы взаимодействия, приводящие к появлению быстрозатухающих гармоник излучения. Наиболее адекватно тепловое воздействие описывает интенсивность I(SPTA). Принято считать, что диагностические уровни интенсивности не вызывают заметного увеличения температуры тканей.
Кавитация, под которой понимается процесс роста, колебаний и схлопывания газовых пузырьков в поле акустической волны, обычно возникает в тех случаях, когда используется ультразвук высокой интенсивности при непрерывном излучении. При использовании импульсного излучения возможности появления кавитации весьма ограничены (она не успевает «развиться»). Кавитационные биоэффекты связаны с I(SPPA), I(SPTP) и механическим индексом, т.е. с отрицательным давлением P− . Значения
последнего в импульсах достаточны для возникновения кавитации, но при большом числе периодов колебаний, характерном для некоторых импульснодоплеровских систем, что требует тщательного контроля при их применении. С другой стороны, пороговые значения возникновения кавитации установлены при исследовании кавитации в газонасыщенных жидкостях, в то время как в тканевых структурах она менее вероятна. Кавитация опасна из-за механического воздействия образующихся ударных волн и акустических течений на клеточные мембраны, а также с химическими реакциями, инициируемыми высвобождением водорода и гидроксильных ионов.
Среди других механизмов действия ультразвука выделяют радиационное давление, влияющее на тканевые структуры (особенно подвижные), перемешивание поглощающих ультразвук жидкостей за счет
