
- •1.2 Акустические волны в скалярных средах
- •1.3 Интенсивность ультразвукового излучения
- •1.4 Биологическое действие ультразвука
- •1.5 Сферические волны
- •Функция Грина и формулы Кирхгофа
- •2.4 Поле сферического фокусирующего преобразователя
- •3.2 Уравнение Вестервельта и волны комбинационных частот
- •3.2. Коэффициент нелинейности биологических сред
- •Таблица 3.2
- •4. ГИДРОДИНАМИЧЕСКИЕ МЕТОДЫ
- •4.1 Уравнения течения вязкой несжимаемой жидкости
- •4.2 Элементы гемодинамики
- •4.3 Аппарат искусственного кровообращения
- •4.4 Вискозиметрия
- •4.5 Измерение артериального давления крови
- •5.1 Методы ультрацентрифугирования
- •5.2 Метод скорости седиментации
- •5.1. Электрические свойства биотканей
- •5.2. Источник внеклеточного поля
- •5.3 Воздействие постоянными и переменными токами и полями
- •5.4 Механизмы поглощения высокочастотных полей
- •Спектр ЭМИ
- •Вопросы для самостоятельного изучения
- •Литература
- •Излучение
- •Ионизирующее
- •6. ПОГЛОЩЕНИЕ ЭМИ
- •6.1 Поглощение СВЧ волн в биологических тканях
- •6.2 Обратные переходы и процессы релаксации
- •6.3 Флуктуационно-диссипационная теорема
- •6.4 Индуктотермия
- •6.5 Биологическое действие высокочастотного ЭМИ
- •Вопросы для самостоятельного изучения
- •Литература
- •7.1 История развития метода
- •7.2 Условие резонанса
- •7.3 Кинетика переходов
- •7.4 Уравнение Блоха
- •7.5 Спектр ЯМР
- •Квадратурное детектирование ЯМР сигналов
- •Чувствительность cw-ЯМР
- •РЧ импульсы и импульсная ЯМР-спектроскопия
- •Чувствительность импульсного ЯМР
- •Применение ЯМР-спектроскопии в биохимии
- •Зависящие от времени процессы в ЯМР
- •Химический анализ
- •Тип движения
- •Область значений частоты, Гц
- •Вибрационные и торсионные движения
- •Латеральная диффузия в мембранах
- •Диффузия в растворах
- •Вращательная диффузия в растворах
- •Конформационные изменения протеинов

частотами ω1 и ω2 в результате их нелинейного взаимодействия со средой появляются волны суммарной (ВСЧ) и разностной (ВРЧ) частоты Ω± =ω1 ±ω2 .
Если учесть нелинейное взаимодействие, которое описывается членами более высокого порядка малости, то спектр частот ультразвукового поля в общем случае будет содержать комбинационные частоты Ω = mω1 ± nω2 , где m и n -
целые числа. Эти волны также могут быть использованы для ультразвуковой медицинской диагностики, что является предметом интенсивных исследований.
3.2. Коэффициент нелинейности биологических сред
Потенциально параметр нелинейности B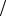 A представляет собой мощный
A представляет собой мощный
инструмент для локальной диагностики состояния мягких тканей. Значения нелинейного параметра некоторых жидкостей и биологических сред приведены в табл.1.2. Из данных табл.1.2 следует, что для биологических жидкостей величина нелинейного параметра B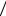 A около 6, у мягких тканей с низким
A около 6, у мягких тканей с низким
cодержанием жира порядка 7 и наибольшее значение порядка 10 в тканях с большим содержанием жира. Исследования паренхимы печени привели к следующей эмпирической зависимости при 37°С
|
|
Таблица 3.2 |
|
Измеренные значения параметра B A для некоторых жидкостей и |
|||
биологических сред |
|
|
|
Среда |
Температура °С |
B A |
|
Вода |
20 |
4,96 |
|
Вода |
40 |
5,38 |
|
3,5% раствор соли |
20 |
5,25 |
|
Макромолекулы в растворе |
20 |
5,3 – 7,6 |
|
Плазма крови |
30 |
5,74 |
|
Кровь |
26 |
6,1 |
|
Нормальные мягкие ткани |
|
6,3 – 8.0 |
|
Глицерин |
20 |
8,8 |
|
Жирные мягкие ткани |
|
9,6 – 11,3 |
|
1015 |
|
B |
=1,378 +0,106x |
w |
+ 4,037x |
f |
, |
(3.8) |
|
ρ c 3 |
|
A |
|||||||
|
|
|
|
|
|||||
0 |
0 |
|
|
|
|
|
|
|
|
где xw и xf - объемное содержание в мягкой ткани воды и жира соответственно.
Нелинейный параметр, однако, чувствителен не только к содержанию жира в мягких тканях. В биомолекулярных растворах величина B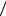 A зависит от
A зависит от
концентрации раствора и очень слабо – от молекулярной массы растворенного вещества. Обнаружена сильная зависимость нелинейных свойств от молекулярного взаимодействия растворителя и растворенного вещества, особенностей их молекулярной структуры и соотношения между свободной и связанной водой. Проведенные исследования выявили также зависимость нелинейного параметра от характера и сложности организации биологических

структур, включая вторичную и третичную структуру белков, структуру клеточных мембран и величину сил межклеточной адгезии. Эти данные свидетельствуют о перспективности исследования и разработки акустических методов визуализации in vivo параметров B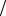 A и ε .
A и ε .
4.ГИДРОДИНАМИЧЕСКИЕ МЕТОДЫ
4.1Уравнения течения вязкой несжимаемой жидкости
Вразделе 1 уже приводились уравнение Навье-Стокса, которое описывает движение элемента объема жидкости с учетом сил вязкого трения
∂v |
|
|
|
|
η |
|
|
ρ |
∂t |
+ (v )v |
= − P +η∆v + (ς + |
3 |
)grad divv , |
||
|
|
|
|
|
|
||
уравнение непрерывности
∂∂ρt + (ρv) = 0,
и уравнение термодинамического равновесия
∂P |
|
∂P |
|
∂ρ |
= c 2 ∂ρ . |
|
= |
|
|||||
∂t |
|
∂ρ |
|
∂t |
0 |
∂t |
|
S |
|
||||
(4.1)
(4.2)
(4.3)
Несложно проверить прямой подстановкой, что уравнение Эйлера можно представить в виде
∂∂t ρvi = − ∂∂Пxik ,
k
где Пik - тензор плотности потока импульса. Из вида этого уравнения понятно, что величина Пik dsk есть поток i -й компоненты импульса, который протекает
через элемент поверхности ds , поэтому Пik |
– это поток i -й |
компоненты |
|||||||||
импульса через единицу поверхности, перпендикулярную к оси |
xk . В случае |
||||||||||
вязкой жидкости тензор потока импульса описывается выражением |
|||||||||||
П |
ik |
= Pδ |
ik |
+ ρv v |
k |
−σ (v) = −σ |
ik |
+ ρv v |
k |
, |
(4.4) |
|
|
i |
ik |
i |
|
|
|||||
так что слагаемое
σik = −Pδik +σik(v) ,
называют тензором напряжений, а σik(v) - вязким тензором напряжений. Єта
сумма, дающая вклад в полній тензор плотности потока импульса, определяет ту часть потока, которая не связана с непосредственным переносом импульса вместе с передвигающейся жидкостью. Тензор вязких напряжений имеет такой же вид, как и у твердых тел
σ (v) =η( |
∂vi |
+ |
∂vk − |
2 |
δ |
∂vl |
) +ςδ |
∂vl . |
|
|
3 |
||||||||
ik |
∂x |
k |
|
∂x |
|
ik ∂x |
|
ik ∂x |
|
|
|
|
i |
|
|
l |
|
l |
|
Эти уравнения позволяют описать все движения вязкой несжимаемой

жидкости. В частности, если жидкость несжимаема, то из уравнения (4.2) находим divv = 0 . Тогда можно пользоваться уравнением движения в виде
|
|
1 |
|
η |
|
|
(v )v |
= − |
|
P + |
|
∆v . |
(4.5) |
ρ |
ρ |
4.2 Элементы гемодинамики
Кровь представляет собой вязкую жидкость с динамической вязкостью в норме η =4-5 мПа·с. При патологии она колеблется от 1,7 до 22,9 мПа·с.
Поэтому рассмотрим вначале задачу о стационарном течении вязкой жидкости по трубе произвольного сечения, которое одинаково по всей длине трубы. Будем считать ось x направленной вдоль оси трубы, тогда скорость жидкости направлена везде по оси x и является функцией только y и z . Тогда уравнение
непрерывности удовлетворяется тождественно, а y - и z -компоненты
уравнения (4.4) приводят к условию постоянства давления по сечению трубы: ∂P ∂y = ∂P
∂y = ∂P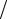 ∂z = 0 . Остается x -компонента уравнения (4.4), которая имеет вид
∂z = 0 . Остается x -компонента уравнения (4.4), которая имеет вид
∂2v + ∂2v = 1 dP . ∂y2 ∂z2 η dx
Левая часть этого уравнения зависит только от y и z , а правая может зависеть
только x . Такое уравнение может иметь решения только в случае, если его левая и правая части являются постоянными величинами. В частности dP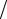 dx = const = − ∆P
dx = const = − ∆P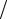 l , где ∆P - падение давления на участке с длиной l .
l , где ∆P - падение давления на участке с длиной l .
Таким образом, распределение скоростей в потоке жидкости в трубе определяется двухмерным уравнением типа ∆v = const с граничным условием v = 0 на контуре сечения трубы. Для трубы с круговым сечением начало координат естественно выбрать на оси трубы и перейти к цилиндрическим координатам. Воспользовавшись выражением для оператора Лапласа в цилиндрических координатах, получаем
1 d |
(r dv) = − |
∆P . |
||
|
|
|||
r dr |
||||
dr |
ηl |
|||
Решение этого уравнения получаем после интегрирования v = − 4∆ηPl r2 +C1 ln r +C2 .
Постоянная C1 = 0, поскольку скорость должна оставаться конечной по всему
сечению трубы, включая ось. C2 |
находим из требования v = 0 при r = R |
|||||
v = |
∆P |
(R2 − r2 ) = v0 |
(1− |
r2 |
), |
|
4ηl |
R2 |
|||||
|
|
|
|
|||
где R - радиус трубы. Таким образом, скорость распределена по сечению трубы по параболическому закону.
Зная распределение скоростей, можно найти количество (объем) жидкости Q , протекающей за единицу времени через поперечное сечение трубы (расход
жидкости). Для этого надо просуммировать расход жидкости через каждый кольцевой элемент площади сечения трубы
Q = 2π ∫R rvdr =2π |
∆P |
∫R |
(R2r − r3 )dr = |
π∆P R4 . |
(4.6) |
|
|||||
0 |
4ηl 0 |
|
8ηl |
|
|
Это выражение позволяет понять принцип действия некоторых лекарственных препаратов, понижающих кровяное давление. Как видим, при заданном расходе крови Q это можно сделать, либо увеличивая радиус кровеносного сосуда
(сосудорасширяющие препараты), либо уменьшая вязкость при помощи препаратов, разжижающих кровь.
При самом общем описании кровеносной системы человека полезно воспользоваться очевидной аналогий расхода крови с силой тока и разности давлений с разностью потенциалов. Таким способом можно ввести понятие о гидравлическом сопротивлении
Q = |
∆P |
, |
Z = |
8ηl |
. |
|
Z |
|
|
πR4 |
|
При последовательном и параллельном соединении сосудов гидравлические сопротивления складываются точно так же, как и электрические. Кроме того, при постоянном расходе крови для работы, совершаемой за время t против сил вязкого трения, можно сразу записать выражение
A = ∆PQt = |
∆P2 |
t = ZQ2t . |
(4.7) |
|
Z |
||||
|
|
|
Допустим, что для нормальной работы какого-либо органа минимально необходим расход крови Q . Тогда для обеспечения при последовательном
соединении N кровеносных сосудов сердце совершит за время t работу
A = NZQ2t .
При параллельном соединении кровеносных сосудов полный расход делится между N сосудами, в результате чего работа равна
A = NZ(Q / N)2 t = N −1ZQ2t .
Таким образом, постоянно разветвляющаяся система кровеносных сосудов представляется очень целесообразной с точки зрения минимизации работы сердца несмотря на то, что каждая бифуркация кровеносного сосуда представляет собой потенциальный источник турбулентного течения.
Рассмотрим теперь самую простую гидродинамическую модель кровеносной системы, которая позволяет установить связь между ударным объемом крови Vу (объем крови, выбрасываемый желудочком сердца за одну
систолу), гидравлическим сопротивлением периферической части системы кровообращения X0 и изменением давления в артериях. Артериальная часть
системы кровообращения моделируется упругим резервуаром с коэффициентом упругости k . Тогда объем крови, находящейся в упругом резервуаре, зависит от давления по следующему соотношению:
V =V0 + kP
где V0 - объем резервуара в отсутствие давления. Отсюда
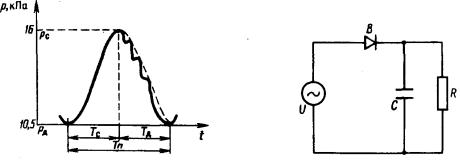
dVdt = k dPdt .
Обозначим через Q расход крови, поступающей из сердца в упругий резервуар (артерии), а через Q0 – расход крови, вытекающей из резервуара в периферическую систему (артериолы, капилляры). На основании закона
Пуазейля можно записать Q |
= (P − P )X |
−1 |
, где P - венозное давление, которое |
|||
0 |
В |
|
0 |
|
|
В |
может быть принято равным нулю. |
Если гидравлическое сопротивление X0 |
|||||
периферической системы постоянно, то справедливо, очевидно, уравнение |
||||||
|
Q = k dP + |
|
P |
. |
||
|
|
|
||||
|
|
dt |
|
|
X0 |
|
Проинтегрируем это уравнение по периоду пульса от 0 до TП . Этим моментам времени соответствует одно и то же минимальное диастолическое давление PД :
T |
PД |
1 |
PД |
||
∫П |
Qdt = ∫ dp + |
∫ |
pdt . |
||
X0 |
|||||
0 |
P |
0 |
|
||
|
Д |
|
|
|
|
Интеграл с равными пределами равен нулю, поэтому
T |
1 |
T |
|
|
∫П Qdt = |
∫П |
pdt . |
||
X0 |
||||
0 |
0 |
|
Экспериментальная кривая, показывающая временную зависимость давления в сонной артерии, приведена на рис.4.1 (сплошная линия). На рисунке показан период пульса, длительность систолы и диастолы и максимальное систолическое давление PC . Интеграл в левой части получившегося уравнения
равен ударному объему крови Vу . Он может быть найден экспериментально,
равно как и интеграл от давления, что позволяет вычислить гидравлическое сопротивление периферической части системы кровообращения.
Во время систолы (сокращение сердца) происходит расширение упругого резервуара, после систолы (диастола) – отток крови к периферии, причем Q = 0,
поскольку желудочек запирается сердечным клапаном. Для этого периода p = pC exp −t (kX0 ) .
(kX0 ) .
а) |
|
|
|
б) |
|
|
|
|
Рис.4.1 Давление в сонной артерии (а) и эквивалентная электрическая схема (б) однокамерной модели
