
- •1.2 Акустические волны в скалярных средах
- •1.3 Интенсивность ультразвукового излучения
- •1.4 Биологическое действие ультразвука
- •1.5 Сферические волны
- •Функция Грина и формулы Кирхгофа
- •2.4 Поле сферического фокусирующего преобразователя
- •3.2 Уравнение Вестервельта и волны комбинационных частот
- •3.2. Коэффициент нелинейности биологических сред
- •Таблица 3.2
- •4. ГИДРОДИНАМИЧЕСКИЕ МЕТОДЫ
- •4.1 Уравнения течения вязкой несжимаемой жидкости
- •4.2 Элементы гемодинамики
- •4.3 Аппарат искусственного кровообращения
- •4.4 Вискозиметрия
- •4.5 Измерение артериального давления крови
- •5.1 Методы ультрацентрифугирования
- •5.2 Метод скорости седиментации
- •5.1. Электрические свойства биотканей
- •5.2. Источник внеклеточного поля
- •5.3 Воздействие постоянными и переменными токами и полями
- •5.4 Механизмы поглощения высокочастотных полей
- •Спектр ЭМИ
- •Вопросы для самостоятельного изучения
- •Литература
- •Излучение
- •Ионизирующее
- •6. ПОГЛОЩЕНИЕ ЭМИ
- •6.1 Поглощение СВЧ волн в биологических тканях
- •6.2 Обратные переходы и процессы релаксации
- •6.3 Флуктуационно-диссипационная теорема
- •6.4 Индуктотермия
- •6.5 Биологическое действие высокочастотного ЭМИ
- •Вопросы для самостоятельного изучения
- •Литература
- •7.1 История развития метода
- •7.2 Условие резонанса
- •7.3 Кинетика переходов
- •7.4 Уравнение Блоха
- •7.5 Спектр ЯМР
- •Квадратурное детектирование ЯМР сигналов
- •Чувствительность cw-ЯМР
- •РЧ импульсы и импульсная ЯМР-спектроскопия
- •Чувствительность импульсного ЯМР
- •Применение ЯМР-спектроскопии в биохимии
- •Зависящие от времени процессы в ЯМР
- •Химический анализ
- •Тип движения
- •Область значений частоты, Гц
- •Вибрационные и торсионные движения
- •Латеральная диффузия в мембранах
- •Диффузия в растворах
- •Вращательная диффузия в растворах
- •Конформационные изменения протеинов
возникающих акустических потоков и сдвиговые напряжения в структурах, обтекаемых потоками вязких биологических жидкостей. Подавляющее большинство экспериментальных исследований при интенсивностях ультразвука, существенно превышающих диагностические, показало отсутствие биоэффектов на генетическом уровне (данные по облучению эмбрионов млекопитающих in utero).
К настоящему времени установлено, что: а) ультразвук не оказывает заметного биологического действия на ткани млекопитающих при пиковой по пространству и средней по времени интенсивности излучения I(SPTA) ниже 100мВт/см2 и б) даже при более высоких уровнях интенсивности отчетливо выраженные биологические эффекты отсутствуют, если произведение I(SPTA) на полное время экспозиции (как при импульсном, так и при непрерывном излучении) не превышает 50Дж/см2. По этой причине используемые сейчас в диагностике уровни интенсивности I(SPTA) не отличаются от средних по пространству и времени интенсивностей излучения I(SАTA) в терапии, если применяется импульсная модуляция и фокусирование, обеспечивающее локальность воздействия.
1.5 Сферические волны
Акустические поля, связанные с продольными волнами в изотропной среде, являются потенциальными, поэтому колебательные скорости и смещения можно выразить через потенциал скоростей ϕ или потенциал
смещений Φ :
|
|
∂u |
|
|
∂Φ |
. |
(1.13) |
|
v |
= − ϕ = |
|
l |
= |
|
|||
∂t |
∂t |
|||||||
|
|
|
|
|
||||
Для гармонических волн эти потенциалы связаны, очевидно, соотношением
ϕ = iωΦ .
Из уравнения (1.13) следует, что акустическое давление также может быть выражено через потенциалы. В частности
pA = ρ0 |
∂ϕ |
= −ρ0 |
∂2Φ |
. |
(1.14) |
|
∂t |
∂t2 |
|||||
|
|
|
|
Оба потенциала удовлетворяют обычному волновому уравнению вида
∆ϕ − |
1 |
∂2ϕ |
= 0. |
(1.15) |
||
c0 |
2 |
∂t2 |
||||
|
|
|
||||
Если волновое движение происходит по гармоническому закону exp(−iωt), то
∆ϕ(r) + k 2ϕ(r) = 0 . |
(1.16) |
Это уравнение носит название уравнения Гельмгольца.
В сферических координатах общее волновое уравнение (1.16) имеет вид
1 |
|
∂ |
2 |
∂ϕ |
|
1 |
|
∂ |
∂ϕ |
|
1 |
∂2ϕ |
|
1 |
∂2ϕ |
|
|
|||
|
|
|
r |
|
|
+ |
|
|
|
sinϑ |
|
+ |
|
|
= |
|
|
|
. |
(1.17) |
r2 |
|
∂r |
|
∂r |
|
r2 sinϑ ∂ϑ |
∂ϑ |
|
r2 sin2 ϑ ∂φ2 |
|
c0 |
2 |
∂t2 |
|
|
|||||
В соответствии с симметрией задачи изменения потенциала по углам ϑ и φ не происходит, поэтому уравнение (1.17) можно представить в виде

∂2∂(rr2ϕ) = c10 2 ∂2∂(tr2ϕ) .
Общее решение этого одномерного волнового уравнения будет иметь вид решения д’Аламбера
ϕ(r,t) = |
A |
f (t ± |
|
r |
). |
|
||
|
|
|
|
|||||
|
r |
|
c |
|
||||
|
|
|
0 |
|
волне, а знак «+» – |
|||
Знак «–» соответствует расходящейся сферической |
||||||||
сходящейся. Для гармонической волны |
A |
|
|
|
||||
ϕ(r,t) =ϕ(r)e−iωt = |
e−i(ωt−kr ) . |
(1.18) |
||||||
|
||||||||
|
|
|
r |
|
||||
где ϕ(r) - амплитуда потенциала, которая является |
решением уравнения |
|||||||
Гельмгольца.
Рассмотрим теперь возбуждение волн малой колеблющейся сферой радиуса a , что позволит в дальнейшем рассчитывать волны, возбуждаемые преобразователями различных форм. По определению потенциала скоростей
v(r) = −∂ϕ(r) |
= − Aeikr (ikr −1) . |
|
||
∂r |
|
r2 |
|
|
Если известна амплитуда радиальных колебаний поверхности сферы |
|
|||
v(a) = − Aeika (ika −1) , |
|
|||
|
|
a2 |
|
|
то можно определить постоянную A , в результате чего выражение (1.18) для |
||||
амплитуды потенциала приобретает вид |
|
|||
ϕ(r) = − |
|
v(a)a2 |
eik (r−a) . |
(1.19) |
|
|
|||
|
r(ika −1) |
|
||
По существу этим задача об излучении звука пульсирующей сферой решена, поскольку в соответствии с (1.14) выражение (1.19) позволяет вычислить амплитуду акустического давления
P(r) = iωρ |
|
v(a)a2 |
eik (r−a) |
(1.20) |
|
0 |
r(ika −1) |
||||
|
|
|
и, в соответствии с определением потенциала (1.13), амплитуду колебательной скорости
vr (r) = v(a)a2 |
ikr −1 eik (r−a) . |
(1.21) |
r2 |
ika −1 |
|
Эти выражения приводят к следующему значению для эффективного акустического импеданса, который по определению равен
z = |
P |
= ρ |
c |
|
ikr |
|
= ρ |
c |
|
k 2r2 −ikr |
|
|
|
ikr −1 |
|
k 2r2 +1 |
|||||||
|
vr |
0 |
|
0 |
0 |
|
0 |
||||
и оказывается комплексным. |
|
|
|
|
|
|
|
|
|
||
Отметим, что вдали |
от |
источника, |
где kr >>1, волновой импеданс |
||||||||
приближается к z0 = ρ0c0 . Однако в случае малых источников в области вблизи источника (ka ≤ kr <<1) волновой импеданс становится чисто мнимым, и в этой

области вещественная часть потока энергии очень мала. Из-за очень малого вещественного потока энергии вблизи источника трудно возбудить акустические волны при диаметре источника, намного меньшем длины волны. Чтобы изложить это другим путем, определим среднюю по времени интенсивность излучения радиально колеблющейся сферы, воспользовавшись выражением для вектора Пойнтинга ультразвуковых волн. Тогда вблизи сферы
|
|
|
|
|
|
1 |
|
|
1 r |
|
|
|
2 |
|
1 r |
2 v(a)2 a2 |
(ka)2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
I |
= Pv |
= |
4 |
(Pv |
+ P v) = |
2 r |
|
vr |
|
|
Re z ≈ |
2 r z0 |
r2 |
|
. |
(1.22) |
|||
|
|
|
1+ (ka)2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В соответствии с выражением (1.22) интенсивность излучения всегда пропорциональна площади излучающей поверхности. Однако плотность потока энергии при заданной амплитуде колебаний становится очень малой при ka → 0 .
При изменении r |
реактивная мощность не сохраняется и в случае сферического |
преобразователя |
становится преобладающей при ka <<1. В этом случае |
давление (1.20) в преобразователе сдвинуто по фазе почти на π/2 по отношению к колебательной скорости (1.21) и очень мало, а эффективный импеданс вблизи преобразователя является индуктивным и равен −ikz0r . Иными словами,
активная нагрузка на преобразователь близка к нулю и при любой амплитуде колебаний интенсивность излучения стремится к нулю.
Эти выводы сохраняются также и в случае плоского преобразователя и преобразователей других форм. Чтобы достичь эффективного возбуждения в среде акустических волн, размер преобразователя (в данном случае его диаметр) должен быть порядка половины длины волны или более.
Функция Грина и формулы Кирхгофа
Кратко остановимся на процедуре вывода функции Грина, которая будет использована далее для анализа дифракции волн, возбуждаемых преобразователями. Итак, из сферически симметричного решения волнового
уравнения |
следует, |
|
что |
|
потенциал |
в |
|
точке x, y, z продольной волны, |
||||||||||||||
вызванной источником, находящимся в точке x , y |
, z |
, может быть записан в |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ ′ ′ |
|
|
|
||
виде |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
ik |
|
r |
−r′ |
|
|
|
′ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
′ |
2 |
|
′ 2 |
′ 2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
G(r − r ) = |
|
|
r − r′ |
|
e |
|
|
|
|
, |
R = |
r − r |
|
= (x − x ) |
|
+ |
(y − y ) |
+ (z − z ) |
. |
|||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Иными словами, это выражение является решением волнового уравнения для потенциала при наличии точечного источника волн с координатами r′
∆G + k |
|
G = δ(x − x , y − y , z − z ) = δ(x − x )δ(y − y )δ(z − z ) = δ(r − r ) , |
(1.23) |
||||||||
|
2 |
′ |
′ |
′ |
′ |
′ |
′ |
′ |
|
|
|
где производные по-прежнему берутся относительно переменных |
x, y, z . |
||||||||||
Функция δ(r − r ) является трехмерной дельта-функцией Дирака, |
а функция |
||||||||||
|
|
′ |
|
|
|
|
|
|
|
|
|
G есть так называемая функция Грина свободного пространства. |
|
|
|
|
|||||||
Для |
|
нахождения |
постоянной |
A проинтегрируем |
уравнение |
(1.23) |
по |
||||
объему малой сферы радиусом |
a , |
включающей в себя точку x , y , z |
. |
По |
|||||||
|
|
|
|
|
|
|
|
′ ′ |
′ |
|
|
определению дельта-функции получаем
∫a→0 (∆G + k 2G)dr =1.
Первый интеграл в этом выражении в силу теоремы Гаусса сводится к интегралу по поверхности сферы. Если ввести новую переменную
интегрирования R = r − r′, то при a → 0 этот интеграл равен
|
|
eikR |
|
R |
|
G dSa = A |
∫Sa R2 |
(ikR −1) |
R |
dSa = −4πA. |
|
∫Sa |
|
|
|
||
Второе слагаемое в подынтегральном выражении при a → 0 стремится к нулю, поэтому постоянная A = −1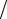 4π , а функция Грина свободного пространства
4π , а функция Грина свободного пространства
равна
G(R) = − |
1 |
eikR . |
(1.24) |
|
4πR |
||||
|
|
|
Используя уравнение (1.23), которому удовлетворяет функция Грина, теперь несложно убедиться, что интегральное выражение вида
|
|
′ |
′ |
′ |
ϕ(r ) = ∫V ′ |
G(r |
− r ) f (r )dr |
||
представляет собой решение уравнения Кирхгофа |
|
|||
∆ϕ + k 2ϕ = f (r ) |
(1.25) |
|||
с распределенными в некотором объеме V ′ источниками излучения. В этом можно убедиться прямой подстановкой выражения для потенциала в уравнение (1.25), если учесть уравнение (1.23), которому удовлетворяет функция Грина
(∆ + k 2 )∫V ′ G(r − r′) f (r′)dr′ = ∫V ′[∆G(r − r′) + k 2G(r − r′)] f (r′)dr′ = f (r ) .
Пространственное распределение объемных источников излучения задается
функцией объемных источников f .
Теперь будем искать решение для потенциала, обусловленного волнами, возбуждаемыми некоторой активной (рабочей) поверхностью (ультразвукового преобразователя). В этом случае в уравнении (1.25) величина f (r ) = 0 , а
источники излучения являются не объемными, а поверхностными. Используем теорему Грина, для чего умножим уравнение (1.25) на G и вычтем результат из произведения уравнения (1.23) на ϕ(r ). Полученное в результате уравнение
проинтегрируем попроизвольномуобъему V , тогда
′ |
|
|
|
ϕ(r ) = ∫V |
(ϕ∆G −G∆ϕ)dr = ∫V |
(ϕ G −G ϕ)dr = |
|
|
= ∫S (ϕ G −G ϕ)dS . |
(1.26) |
|
где снова использована теорема Гаусса. Мы видим, что потенциал ϕ можно
найти в любой точке r′, если известны его значения и значения его производной на любой замкнутой поверхности, ограничивающей объем V . Иными словами, для волнового поля результат вычисления потенциала не будет зависеть от выбранной поверхности. Этот факт называют интегральной теоремой Гельмгольца. Если в первом интеграле формулы (1.26) произвести замену r ↔ r′ и учесть объемные источники, то получим общую формулу Кирхгофа
ϕ(r ) = ∫S [ϕ(r′) ′G(r′− r ) −G(r′− r ) ′ϕ(r′)dS′+ ∫V ′ G(r − r′) f (r′)dr′. (1.27)

Более того, если объем V содержит какие-то иные замкнутые поверхности, на которых известны значения потенциала и его производных, то в выражении (1.27) под поверхностью S нужно понимать все такие замкнутые поверхности. В этом случае интеграл в (1.27) представляет сумму интегралов по всем поверхностям, а само решение (1.27) является справедливым для области Ω, ограниченной всеми поверхностями.
Рассмотрим теперь плоский (поршневой) преобразователь площадью S1 в экране площадью S2 (рис.1.1) в отсутствие объемных источников. Оставшуюся
часть поверхности, окружающей рассматриваемый объем, обозначим через Σ. Тогда для бесконечно удаленной поверхности Σ, т.е. при r′ → ∞, функция ϕ(r′)
асимптотически представляет собой сферически расходящуюся волну, как и функция Грина. В этом случае вклад в интеграл, который дает поверхность Σ в выражении (1.27), становится равным нулю, поскольку два слагаемых в подынтегральном выражении взаимно уничтожаются. Следовательно, вклад в интеграл от поверхности, удаленной на бесконечность, можно не учитывать.
Это положение называется условием излучения Зоммерфельда.
Пусть потенциал и его градиент на поверхности экрана S2 равны нулю.
Это эквивалентно предположению, что в жидкости на экране как давление, так и нормальное смещение равно нулю. При этих условиях и в отсутствие объемных
источников ( f (r ) = 0 ) |
излучающей будет только поверхность S1 , так что |
||||||||
выражение (1.28) можно записать в виде |
|
|
|
|
|
|
|||
|
′ ′ |
′ |
|
′ |
|
′ ′ |
′ |
. |
(1.28) |
ϕ(r ) = ∫S |
[ϕ(r ) G(r |
− r ) −G(r |
− r ) ϕ(r )dS |
|
|||||
1 |
|
|
|
|
|
|
|
|
|
Это выражение также часто называют формулой Кирхгофа. Ее иногда применяют для оценок на практике, но она не является строго корректной, поскольку не может быть самосогласованной. Физически формула (1.28) не учитывает так называемые краевые поля, которые обязательно приводят к
ненулевым давлениям (ϕ ≠ 0) и/или смещениям ( ′ϕ ≠ 0) на экране S2 . Математически обе эти величины не могут быть заданы произвольно на всех
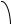 ϑ
ϑ
Рис.1.1 Расположение излучающей поверхности S1 и экранов S2 и Σ (для всех
поверхностей нормаль направлена вовне из объема V , в частности, на поверхности преобразователя – внутрь него)
окружающих поверхностях – это приведет к переопределению потенциала, как функции.
Не является строго корректным даже задание Φ и ′Φ на преобразователе. Однако для преобразователей, конечные размеры которых много больше длины волны, обычно допустимо использовать простое условие, относящееся к плоским волнам ∂ϕ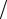 ∂z′ = ikϕ на преобразователе, и считать
∂z′ = ikϕ на преобразователе, и считать
∂ϕ ∂z′ =ϕ = 0 на S2 . Если поперечные размеры преобразователяочень велики, то
∂z′ =ϕ = 0 на S2 . Если поперечные размеры преобразователяочень велики, то
граничные условия на экране не очень важны и уравнение (1.29) даетрезультаты, близкие к действительным. Граничные условия на экране приобретают важное значение тогда, когда преобразователь сравнительно мал (т.е. его диаметр порядка или меньше длины волны). Так бывает, например, с малыми элементами электронных фазированных решеток, которые используют в современных устройствах формирования ультразвуковыхизображений.
2.ПОЛЯ УЛЬТРАЗВУКОВЫХ ПРЕОБРАЗОВАТЕЛЕЙ
2.1Формулы Рэлея-Зоммерфельда и Гюйгенса-Френеля
Всвязи с указанными выше противоречиями, возникающими при рассмотрении вопроса об излучении волн поверхностными источниками, лучше найти такую возможность, при которой необходимо задавать на границе только потенциал или его градиент. Иными словами, в формуле для поля излучения в виде поверхностного интеграла предпочтительна такая функция Грина, что G(r′, r ) = 0 или ∂G(r′, r )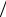 ∂z′ = 0 на преобразователе и его экране (z′ = 0 ). Тогда на
∂z′ = 0 на преобразователе и его экране (z′ = 0 ). Тогда на
преобразователе достаточно задать соответственно только градиент потенциала или потенциал. Для этого рассмотрим две функции
|
′ |
|
|
|
|
′ |
|
′ |
1 |
|
eikR+ |
|
eikR− |
|
|
||
G± (r |
, r ) = G(r − r+ ) ±G(r |
− r− ) = − |
|
( |
R+ |
± |
R− |
) , |
(2.1) |
||||||||
4π |
|||||||||||||||||
R± = |
|
r − r±′ |
|
= |
|
|
. |
|
|
||||||||
|
|
|
(x − x′)2 + (y − y′)2 + (z z′)2 |
|
|
||||||||||||
|
|
|
|
||||||||||||||
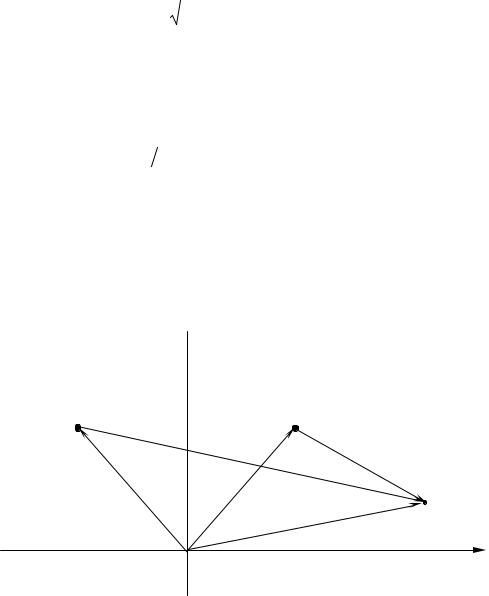
Из вида этих функций понятно, что они описывают такое пространство, в котором появление источника в точке r+′ = (x′, y′, z′) всегда сопровождается
появлением синфазного (+) или противофазного (–) источника в зеркально
отраженной точке r−′ = (x′, y′,−z′) , как показано на рис.2.1. |
|
Несложно убедиться, |
что для синфазных источников на поверхности |
z = 0 величина G+ ≠ 0 , а ∂G+ |
∂z = 0. В соответствии с формулами (1.13) и (1.14) |
это означает, что на этой поверхности всегда равны нулю нормальные смещения, в то время как акустическое давление отлично от нуля. В этом случае говорят, что функция G+ является функцией Грина для
полупространства с абсолютно жесткой границей. Заметим, что функция G+ является точной функцией Грина такого полупространства. В обратном
±δ(r − r′) |
δ(r − r+′) |
||||||||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
r+′ |
||||||
|
|
|
|
|
|
|
|
r − r+′ |
|
|
r−′ |
||||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
r − r−′ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z
Рис.2.1 Взаимное расположение источников и границы раздела пространства

случае противофазных источников потенциального поля, когда G− = 0 и ∂G− 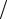 ∂z ≠ 0 при z = 0, можно говорить о полупространстве с абсолютно мягкой
∂z ≠ 0 при z = 0, можно говорить о полупространстве с абсолютно мягкой
границей, на которой всегда отличны от нуля смещения и равно нулю давление. Теперь рассмотрим более подробно случай ультразвукового излучателя, находящегося в абсолютно жестком экране. Понятно, что функции G± (r′, r )
обладают такими же свойствами по переменной r |
′ |
, что и функции G± (r, r ) по |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
переменной r . Тогда из о |
бщей |
формулы Кирхгофа (1.27) в отсутствие |
||||||||||||||||||||||
объемных источников излучения получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
′ |
′ |
′ |
|
′ |
− |
∫S |
|
|
|
|
|
′ |
|
|
′ |
′ |
′ |
= |
(2.2) |
||||
ϕ(r ) = ∫S |
G+ (r |
, r ) ϕ |
(r )dS |
|
2 |
|
G+ (r |
, r ) ϕ |
(r )dS |
|
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
r′−r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
′ |
′ |
|
|
|
eik |
|
|
|
|
|
|
′ |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
= |
|
∫S v(x , y ,0) |
|
|
|
|
|
|
dS |
|
, |
|
|
|
|
|
|||||||
|
2π |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
|
|
|
r′ |
− r |
|
|
|
|
|
|
|
|
|
|
|||||
поскольку теперь смещения и колебательная скорость могут быть ненулевыми только вблизи рабочей поверхности преобразователя, а на экране они везде
равны нулю. При выводе формулы (2.2) мы учли, что нормаль поверхности S′ направлена внутрь преобразователя. Выражение (2.2) называется формулой Релея-Зоммерфельда, которая корректна для плоского поршневого преобразователя, окруженного абсолютно жестким экраном. О плоском преобразователе здесь говорится потому, что введенные функции Грина (2.1) справедливы для полупространства с плоской границей (рис.2.1).
Выбор функции Грина со знаком минус в выражении (2.2), соответствующий абсолютно мягкому экрану, дает решение для потенциала в любой точке с z ≥ 0 в виде
|
1 |
∫S ϕ(x′, y′,0) |
eik |
|
r′−r |
|
(1−ik |
|
|
r′− r |
|
) |
cosϑ dS′, |
|
|||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|||||||||||||||||
ϕ(r ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.3) |
|||
2π |
|
|
( |
|
|
|
) |
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
1 |
|
|
|
r |
′− r |
|
|
|
|
|
|
|||||||
где ϑ - угол между вектором R = r − r′ и осью z , показанный на рис.1.1. В соответствии с выражением (1.14) эта формула определяет связь между акустическими давлениями на поверхности преобразователя и в возбуждаемой волне.
Обычно интерес представляют области, удаленные от преобразователя на
несколько длин волн. В этом случае можно принять, что k |
|
r′− r |
|
>>1, и написать |
|||||||||||||
|
|
||||||||||||||||
формулу (2.3) в форме Гюйгенса-Френеля: |
|
|
|
|
r′−r |
|
|
|
|
|
|
|
|
|
|
||
|
ik |
′ ′ |
|
eik |
|
|
|
|
cosϑ dS |
′ |
|
|
|
||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||
ϕ(r ) = − |
|
∫S ϕ(x , y ,0) |
|
|
|
|
|
|
|
. |
(2.4) |
||||||
2π |
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||
|
1 |
|
r |
′− r |
|
|
|
|
|
|
|||||||
Отметим, что результаты, даваемые формулами (2.3) – (2.4), не являются точными для волн в твердом теле, поскольку предполагается, что потенциал на плоскости вне преобразователя равен нулю. Это предположение о нулевом потенциале в случае жидкости эквивалентно допущению, что нормальное упругое напряжение равно нулю на плоскости z = 0 вне преобразователя. Но нулевой потенциал для продольных волн не означает, что все упругие напряжения обращаются в нуль в твердом теле и их нужно учитывать отдельно.
Наконец, аналогичные выражения для источника v(x′, y′,0) или
ϕ(x′, y′,0) , изменяющегося произвольно во времени, можно найти, выполнив
обратное преобразование Фурье или Лапласа выражения (2.2)или (2.4). Результат для преобразователя в абсолютно жестком экране, например, таков:
ϕ(t;r ) = |
1 |
|
∫S |
1 |
v(t − |
R |
)dS′ |
|
|
2π |
|
|
|
|
|||||
|
1 |
R |
c0 |
′ |
= (x , y ,0) |
||||
где v является функцией времени, |
заданной в каждой точке r |
||||||||
|
|
|
|
|
|
|
|
′ ′ |
|
поверхности преобразователя.
Таким образом, если величина смещений или потенциал равны нулю на окружающем преобразователь экране, но известны на его поверхности, то можно найти потенциал в произвольной точке в произвольный момент времени. Приведенные здесь выражения служат основой для расчета полей преобразователей, используемых в ультразвуковой медицинской томографии. Отличия между поведением преобразователя в абсолютно жестком и абсолютно мягком экранах еще будут обсуждаться, сейчас заметим лишь, что примером преобразователя в жестком экране может служить преобразователь в воде, окруженный круглой металлической пластиной, импеданс которой значительно больше импеданса воды. Примером преобразователя в абсолютно мягком экране может служить преобразователь, контактирующий с поверхностью тела пациента. Иной пример – это малый преобразователь или один элемент решетки идентичных преобразователей с периодом в одну длину волны или более, отделенных от ванны с водой майларовой (капроновой) пленкой, так что с одной стороны пленки вода, а с другой– воздух.
На практике режим работы решетки преобразователей зависит от расстояния между ее элементами и заполнителя. Таким образом, угловая характеристика элемента решетки преобразователей оказывается промежуточной между характеристикой преобразователя в абсолютно мягком экране и характеристикой преобразователя в абсолютно жестком экране.
2.2 Осевое распределение поля плоского поршневого преобразователя
Воспользовавшись общими результатами для полей излучения, рассмотрим поле плоского круглого поршневого преобразователя радиуса a , излучающего волны в скалярную среду (жидкость). Для описания ультразвуковых полей, применяемых в медицинской диагностике и терапии, в наибольшей степени подходит условие излучения в абсолютно мягком экране, поскольку граница «воздух-поверхность тела» с очевидностью очень хорошо удовлетворяет этому условию. Однако общие принципы расчета и приближения, которые делают при рассмотрении ультразвуковых полей, одинаковы для преобразователей в любом экране, поэтому ограничимся случаем абсолютно жесткого экрана, при котором исходное выражение для потенциала несколько проще. При этом все практически важные выводы будут справедливы и для преобразователя в мягком экране.
Положим, что колебательная скорость на поверхности преобразователя v(x′, y′,0) = v0 однородна по радиусу, а вне этой поверхности равна нулю, тогда

|
a |
|
eik |
|
r′−r |
|
′ |
′ |
|
|
|
|
|
|
|
||||||||
ϕ(r ) = v0 |
∫0 |
|
|
r′ |
|
− r |
|
r dr |
|
. |
(2.5) |
|
|
|
|
||||||||
Рассмотрим вначале распределение поля на оси преобразователя, тогда
расстояние от точки с координатой |
z на оси до |
элементов кольца между |
||||||||
окружностями с радиусом r′ и |
r′+ dr′ равно |
R = |
|
r′− r |
|
= |
|
и |
||
|
|
r′2 + z2 |
||||||||
|
|
|||||||||
RdR = r dr |
′ |
. Таким образом, амплитуда волны в точке |
z на оси равна |
|||||||
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
eik |
|
2 |
|
2 |
|
−eikz |
|
|
ϕ(0, z) = v0 |
|
a |
∫+z |
|
eikR dR = v0 |
|
a |
+z |
|
|
|
= |
||||
|
|
|
|
z |
|
|
|
|
|
ik |
|
|
||||
= 2v0k −1eik ( |
|
a2 +z2 |
+z ) 2 sin{k( |
a2 |
+ z2 |
|
|
|
− z) 2}. |
|||||||
Продифференцировав это выражение по z , несложно показать, что
|
|
∂ϕ(0, z) |
|
|
|
|
|
z |
|
|
ik |
|
|
|
|
|
ikz |
|
|
|
|
a2 +z2 |
|||||
v |
(0, z) = − |
∂z |
= v |
e |
|
− |
|
|
|
e |
|
|
. |
|
|
|
|
||||||||||
|
a2 + z2 |
||||||||||||
z |
|
0 |
|
|
|
|
|
|
|
|
|
(2.6)
(2.7)
Эта формула сводится к vz = v0 при z = 0, тогда как амплитуда величины ϕ(0,0) равна 2v0k −1 sin{ka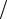 2}. Как мы увидим позднее, величины vz (r, z) и ϕ(r, z)
2}. Как мы увидим позднее, величины vz (r, z) и ϕ(r, z)
быстро изменяются с радиусом вблизи от преобразователя. Выражение (2.6) позволяет вычислить величину акустического давления путем простого умножения на −iρ0ω :
P(0, z) = −2iρ c v |
eik ( |
a2 +z2 |
+z ) 2 sin{k( |
a2 |
+ z2 |
− z) 2}. |
(2.8) |
||
0 |
0 |
0 |
|
|
|
|
|
|
|
При рассмотрении полей на больших расстояниях от преобразователя,
когда z2 >> a2 , всегда используют френелевское или параксиальное приближение. А именно, в этой области можно разложить квадратные корни в выражениях (2.7) и (2.8) до второго порядка малости по a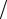 z , учесть эти члены в
z , учесть эти члены в
фазовых множителях и отбросить в амплитудных. Тогда для колебательной скорости и акустического давления получаем
vz (0, z) = v0 (eikz −eik ( z+a2 2 z ) )= −2iv0eikz+iπa2 2 zλ sin |
πa2 |
, |
(2.9) |
|
|
πa2 . |
2zλ |
|
|
P = −2iρ0c0v0eikz+iπa2 2 zλ sin |
|
|
(2.10) |
|
|
2zλ |
|
|
|
Отсюда вытекает выражение для интенсивности излучения на оси преобразователя
|
I(0, z) = 2ρ0c0v0 2 sin2 |
|
lF |
|
|
|
|
|
|
|
|||||||||
|
2z |
|
|
|
|
|
|||||||||||||
где lF =πa2 |
λ - длина зоны |
Френеля. |
|
|
|
|
|
|
|
|
|||||||||
Часто |
вводят также безразмерное |
||||||||||||||||||
расстояние или параметр Френеля, который имеет вид |
|
|
|||||||||||||||||
|
|
S = zλ a2 |
=πz lF . |
|
|
|
|
|
|
(2.11) |
|||||||||
Область, в |
которой z >> lF , |
т.е. |
безразмерный |
параметр |
S >>1, называется |
||||||||||||||
областью дальнего поля или зоной Фраунгофера. В зоне Фраунгофера |
|||||||||||||||||||
|
I(0, z) = |
1 |
ρ |
c |
v |
2 |
l |
2 |
= |
1 |
|
ρ |
c |
v |
2 |
|
π |
2 |
|
|
2 |
|
|
F |
2 |
|
|
|
|
(2.12) |
|||||||||
|
|
0 |
0 |
|
0 |
z |
|
|
0 |
0 |
|
0 |
|
S |
|
||||

плотность потока акустической энергии уменьшается с расстоянием пропорционально z−2 .
Область, в которой z <π −1lF и S <1, называется зоной Френеля. В зоне
Френеля поле имеет резко осциллирующий характер, в то время как дальняя зона Фраунгофера отличается плавным убыванием амплитуды колебаний с
расстоянием по закону x−1 , который характерен для сферически расходящихся волн. При S <1 потенциал акустического поля, а вместе с ним акустическое давление и колебательная скорость, максимален на оси в точках, для которых аргумент синуса в выражениях (2.10) и (2.11) равен (2m +1)π 2. Из выражения
2. Из выражения
(2.6) следует, что координата z в точке, где потенциал максимален, равна
zmax = |
a2 |
− |
(2m +1)λ |
≈ |
a2 |
при ka >> (2m +1)π . |
(2.13) |
|
(2m +1)λ |
4 |
(2m +1)λ |
||||||
|
|
|
|
|
Приближенное выражение в соотношении (2.13) является точным для определения максимумов акустического давления (2.10) и колебательной скорости (2.9). Теперь видно, что эти выражения и само приближение Френеля справедливо, как правило, при очень больших значениях ka , когда диаметр преобразователя составляет много длин волн.
В точках (2.13) максимума амплитуда колебаний (скорости и давления) равна своему удвоенному значению на преобразователе. Скорость и давление обращаютсявнульвточкахскоординатами
zmin = |
a2 |
, |
при ka >> 2mπ . |
|||
|
||||||
Заметим, что при малых z |
|
2mλ |
|
|
|
|
поля на оси быстро изменяются с расстоянием. Это |
||||||
обусловлено тем, что величина kR = k |
|
r′2 + z2 |
быстро изменяется с радиусом |
|||
при малых z , вследствие чего волновые |
поля, излучаемые отдельными |
|||||
кольцевыми элементами |
преобразователя, |
попеременно складываются и |
||||
вычитаются. Однако при больших R , таких, что R ≈ z + r′2 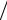 2z , с изменением
2z , с изменением
радиуса r′ происходят лишь малые изменения kR = k 
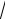 r′2 + z2 , так что все излучение от диска складывается в одной фазе. Это происходит, когда разность проходимых лучами путей меньше половиныдлины волны: S >1.
r′2 + z2 , так что все излучение от диска складывается в одной фазе. Это происходит, когда разность проходимых лучами путей меньше половиныдлины волны: S >1.
Условие z = a2 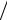 λ ( S =1) точно соответствует условию m =0 (последний
λ ( S =1) точно соответствует условию m =0 (последний
максимум) в выражении (8). Назовем эту точку S =1 точкой пересечения зон Френеля и Фраунгофера или пределом Френеля. Внутри зоны Френеля следует ожидать резких изменений амплитуды смещений в зависимости от радиуса. Однако вне радиуса a эти поля быстро спадают до нуля, так что большая часть
энергии содержится в пределах радиуса a . Таким образом, при z < a2 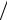 λ или
λ или
S <1 пучок в основном сохраняет свой первоначальный диаметр. Предположим теперь, что для приема прошедшей волны используется другой преобразователь такого же размера. В этом случае резкие изменения поля по диаметру приемного преобразователя сглаживаются и сигнал, регистрируемый приемным преобразователем, изменяется в пределах зоны Френеля очень слабо. Это в равной степени относится и к случаю, когда в качестве излучателя и приемника

0 |
0,5 |
1 |
Рис.2.2 Зависимость нормированного поля смещений и скоростей на оси преобразователя от нормированного расстояния S
отраженной без искажений волны используется один и тот же преобразователь, а общая длина пути, проходимого пучком, меньше a2 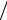 λ.
λ.
График зависимости амплитуды смещения от безразмерного расстояния представлен на рис.2.2 при большом значении ka =100. Этот график построен по точному решению (3), тогда как штриховая линия на рис.2.2 соответствует приближению Френеля. Таким образом, максимальные значения величины смещения при малых значениях S меньше двух, а минимальные значения больше нуля, но по мере возрастания S они приближаются к соответствующему параксиальному, или френелевскому решению.
Использование приближения Френеля удобно, поскольку получаемые с его помощью результаты могут быть выражены только через один параметр S , и оно часто оказывается достаточно точным. Это решение носит универсальный характер и справедливо при значениях ka , используемых во многих практических преобразователях, работающих в изотропных средах; кроме того, для точек, лежащих вне оси, проще проводить вычисления с помощью этих решений, чем с помощью точного решения. Дополнительные графики изменения поля на оси и вне ее приведенына рис.2.3.
2.3 Распределение поля плоского преобразователя в зоне Фраунгофера
Для нахождения полей вне оси преобразователя можем использовать простейший анализ, соответствующий зоне Фраунгофера, полагая по прежнему
z >π −1lF >> a . Начинать удобнее в цилиндрических координатах, введенных
таким образом, что нештрихованные цилиндрические координаты точки (r , z,ψ) соответствуют точке наблюдения, а штрихованные, по которым ведется
интегрирование в (2.2), соответствуют точкам на поверхности преобразователя. Тогда расстояние между точкой наблюдения и точкой на поверхности есть
R = 
 z2 + r 2 + r′2 − 2r r′ cos(ψ′−ψ) =
z2 + r 2 + r′2 − 2r r′ cos(ψ′−ψ) = 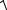
 r2 + r′2 − 2rr′ sinθ cos(ψ′−ψ) .
r2 + r′2 − 2rr′ sinθ cos(ψ′−ψ) .
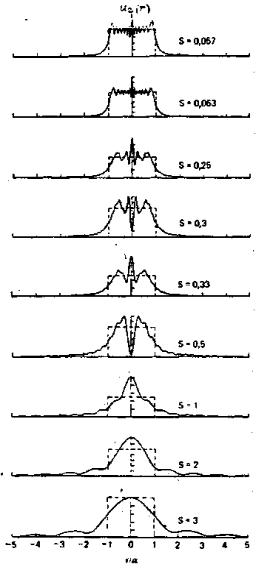
Рис.2.3 Радиальная зависимость смещения при ka =100 и при разных значениях S (штриховые линии – величина смещений и скоростей на преобразователе)
Здесь для точек наблюдения совершен переход к сферическим координатам
путем подстановки z2 + r |
2 = r2 и r = r sinθ , где полярный угол θ = 0 для точек |
на оси преобразователя z . |
|
В приближении Фраунгофера полагают, что r >> r′, а в фазовых членах |
|
оставляют только линейные по малым r′ слагаемые. В результате |
|
|
R = r − r′ sinθ cos(ψ′−ψ) . |
Если по-прежнему учитывать влияние изменения расстояния только на фазовый множитель и положить в знаменателе выражения (1) R = r , то получим
|
v |
0 |
eikr |
2π a |
−ikr′ |
sinθ cos(ψ′−ψ ) |
′ ′ |
′ |
|
ϕ(r,θ) = |
|
|
∫∫e |
|
|
(2.14) |
|||
|
|
|
|
|
|||||
2π |
r |
|
|
dψ r dr . |
|||||
|
0 0 |
|
|
|
|
|
|||
Интеграл по угловой переменной в выражении (2.14) |
является табличным и |
||||||||
вместе с множителем (2π)−1 есть ничто иное, как интегральное представление
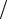
функции Бесселя J0 первого рода нулевого порядка. Поэтому после интегрирования по угловой переменной получаем
eikr a
ϕ(r,θ) = v0 r ∫0 J0 (kr′sinθ)r′dr′.
Наконец, используя интегральное соотношение между функциями Бесселя ∫zJ0 (z)dz = zJ1 (z) , приходим к окончательному выражению для потенциала
смещений волны, возбуждаемой круглым поршневым преобразователем
ϕ(r,θ) = v0a |
2 |
J1 |
(kasinθ) eikr |
. |
(2.15) |
|
|
|
|
|
|||
|
|
kasinθ r |
||||
|
|
|
|
|
||
В соответствии с выражением (2.15) амплитуда колебательной скорости и акустического давления описываются выражениями
v(r, R0 ) = −i2v0 |
πa2eikr |
J1 (kasinθ) |
. |
|
|
|
|||||||||||
r |
|
|
kasinθ |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
πa2eikr J1 (kasinθ) |
|
|
|
||||||||
P(r, R0 ) = −i2c0 ρ0v0 |
|
|
|
|
|
|
|
|
, |
|
|
||||||
r |
|
kasinθ |
|
|
|
||||||||||||
так что интенсивность излучения равна |
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
I(r,θ) = |
1 |
ρ |
c |
v |
2 |
πa2 |
jinc |
2 |
a sinθ |
|
, |
(2.16) |
|||||
2 |
0 |
|
|
|
|
λ |
|
|
|||||||||
|
0 |
0 |
|
λr |
|
|
|
|
|
|
|
|
|
||||
где функция jinc(x) = J1 (2πx) πx . |
Если |
θ → 0, |
то |
значение этой |
функции |
||||||||||||
стремится к единице, а выражение (2.16) совпадает с формулой (2.2), поскольку при θ = 0 величина r = z . Далее, первый нуль интенсивности излучения лежит при ka sinθ =3,83. При ka >>1 величина угла θ1 , соответствующего первому
нулю, очень мала и равнаθ1 = 0,61λ a .
a .
Суммируя, можно сделать вывод, что при z <π −1lF акустический пучок
практически сохраняет свой первоначальный радиус. За точкой S =1 его интенсивность изменяется с углом θ и в диаграмме направленности излучения появляются несколько лепестков. В зоне Фраунгофера интенсивность излучения убывает как r−2 . Эти выводы справедливы и для поля преобразователя,окруженного абсолютно мягким экраном. В этом случае при расчете в качестве исходного необходимо использовать не выражение (2.2), а формулу Гюйгенса-Френеля (2.4). В результате получается выражение, эквивалентное формуле (2.16):
I(r,θ) = |
1 |
ρ |
c |
v |
2 |
πa2 |
2 |
jinc |
2 |
a sinθ |
2 |
θ . |
|||
2 |
|
|
λr |
|
|
|
λ |
cos |
|
||||||
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|||
Таким образом, даже преобразователь с очень малым радиусом, для которого функция jinc(x) является очень широкой, в абсолютно мягком экране дает
угловое распределение с уровнем 3дБ при θ =45°.
Изложенную дифракционную теорию можно также видоизменить применительно к прямоугольным системам. Удобнее всего это выполнить, например, с помощью подхода, основанного на преобразовании Фурье. В этом случае отсутствует простое аналитическое решение для изменения поля произвольного прямоугольного преобразователя, однако существуют
