5. ОСНОВЫ ДИАГНОСТИЧЕСКИХ И ТЕРАПЕВТИЧЕСКИХ ПРИМЕНЕНИЙ ЭЛЕКТРОМАГНИТНЫХ ИЗЛУЧЕНИЙ В МЕДИЦИНЕ
5.1. Электрические свойства биотканей
Биоткань проявляет по крайней мере три важных электрических свойства. Во-первых, в ней существуют свободные носители заряда, и поэтому ее можно считать объемным электрическим проводником электролитического типа. Электропроводность является характерным свойством всех биотканей и можно ожидать, что по картинам распределений электропроводности можно различать структуры и обнаруживать очаги патологии. Далее, ткань не является чисто омической средой. Внеклеточные токи текут не только по межклеточным щелям, но и через клетки, пересекая мембраны. Клеточные мембраны представляют собой естественные емкости, поэтому необходимо учитывать емкость тонких мембран клеток. Наконец, биоткань содержит также связанные заряды, приводящие к диэлектрическим эффектам, и потому кроме терапевтических применений, основанных на этом физическом свойстве, можно, по-видимому, получать изображение распределений относительной диэлектрической проницаемости.
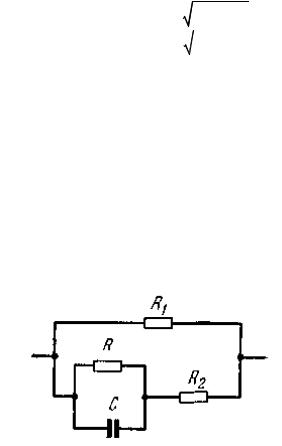
Емкостную поправку к электрическому импедансу мягких тканей легко учесть при помощи эквивалентной электрической схемы (рис.5.1) элемента внеклеточного пространства. Соответствующий импеданс есть
|
Z(ω) |
|
= |
R1(R + R2 ) |
|
|
1+ω2τ2 |
2 |
|
, |
(5.1) |
|
|
|
|
||||||||||
|
|
R + R1 + R2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
1+ω2τ12 |
|
|
|
|||
где R1 - активное сопротивление току |
|
в межклеточном объеме, |
R2 - |
|||||||||
сопротивление клеточной плазмы и межклеточного пространства для той части тока, которая пересекает мембрану, представленную на схеме RC -элементом, R - активное сопротивление мембраны этому же току. Величины
τ1 =τ |
R + R2 |
|
, |
τ2 =τ |
R2 |
||
|
|
||||||
R + R |
+ R |
R + R |
|||||
|
|
|
|||||
|
1 |
|
2 |
|
|
2 |
|
где τ = R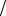
C - постоянная релаксации RC -элемента.
Сдвиг фазы в электрической цепи на рис.5.1 описывается выражением
Рис.5.1 Эквивалентная электрическая схема элементов мягких тканей
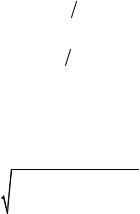
ϕ(ω) = arctg ωτ1 −arctg ωτ2 , |
(5.2) |
В рассматриваемой простой модели импеданс тканей монотонно уменьшается с увеличением частоты от
|
Z(0) |
|
= R1(R + R2 ) |
(R + R1 + R2 ) |
(5.3) |
|||
|
|
|||||||
до |
(R1 + R2 ) . |
(5.4) |
||||||
|
|
Z(∞) |
|
= R1R2 |
||||
|
|
|
||||||
Из формулы (5.1) видно, что чем меньше R1, т.е. чем больше объем внеклеточной жидкости, тем меньше импеданс и диапазон его изменения с частотой, т.е. слабее дисперсия импеданса.
Сдвиг фазы равен нулю при v = 0, ∞ и обладает максимумом на частоте
ω = |
1 |
(1+ |
|
R |
)(1+ |
R |
) |
τ |
R + R |
|
|||||
|
|
|
R |
||||
|
|
|
1 |
2 |
|
2 |
|
Если использовать, например, величину τ ≈ 7мс для нейронной мембраны, то из этого выражения для частоты получим f > 20Гц.
Существует много данных, подтверждающих качественную пригодность эквивалентной схемы рис.5.1 для объяснения электрического импеданса мягких тканей и, в частности, серого вещества мозга. Для него комплексный характер сопротивления обнаруживается, хотя реактивная составляющая мала, а
максимум сдвига фазы ϕ = −7o приходится на диапазон частот 50 – 100 Гц.
Следовательно, в проводимости серого вещества преобладает межклеточная жидкость. По этой причине, в частности, емкостная проводимость не может качественно изменить поля, создаваемые потенциалами действия (спайками) во внеклеточном пространстве серого вещества мозга. Роль реактивной составляющей, вероятно, возрастает в результате распространяющейся депрессии и ишемии, когда, как полагают, уменьшается межклеточное пространство.
О значительности емкостного сопротивления в других мягких тканях свидетельствуют большие значения сдвига фаз (5.2). В частности, в коже
(человека, лягушки) ϕ = −55o , в мышцах кролика ϕ = −65o , в нерве лягушки ϕ = −640 и т.д.. С точки зрения диагностики частотная зависимость импеданса
позволяет оценить, например, жизнеспособность тканей организма, что важно знать для трансплантации тканей и органов. Различие в частотных зависимостях импеданса получается также для ткани в норме и при патологии. Наконец, импеданс тканей и органов зависит от их физиологического состояния. Так, при кровенаполнении сосудов импеданс изменяется в зависимости от состояния сердечно-сосудистой деятельности. Диагностический метод, основанный на регистрации изменения импеданса тканей в процессе сердечной деятельности, называют реографией (или импедансплетизмография). С помощью этого метода получают реограммы головного мозга (реоэнцефалограмма), сердца (реокардиограмма), магистральных кровеносных сосудов и т.д..
Измерения проводят обычно на частоте 30кГц, что соответствует
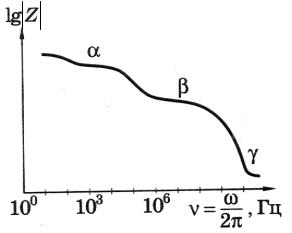
приблизительно пологой части кривой импеданса в α -области на рис.5.2. Дисперсия импеданса (1) в α, β и γ -областях несколько различается из-за
дополнительной частотной зависимости, появляющейся в результате зависимости от частоты диэлектрической проницаемости ε(ω) как
внеклеточной жидкости, так и липидных мембран. Для клеточных мембран это свойство прямо приводит к изменению их емкости C(ω) , которая зависит от
диэлектрической проницаемости среды между «обкладками». Для внеклеточной жидкости в γ -области этот эффект определяется ориентационной
поляризацией молекул воды (частоты порядка 20ГГц), в β -области –
поляризацией крупных полярных молекул (1-10МГц) и в α -области – поляризацией целых клеток (0,1 – 10кГц). Обратные к этим частотам величины представляют собой характерные времена соответствующих процессов. Например, для α -области – это характерное время диффузии ионов внутри клетки, приводящей к ее поляризации.
5.2. Источник внеклеточного поля
Внутренним источником тока в ткани, как в объемном проводнике, является клетка. Будем считать, что вне клетки плотность тока j источников не
имеет, тогда полный средний заряд в любой части объема проводника не изменяется
divj = 0. |
(5.5) |
В однородных изотропных проводниках плотность тока почти всегда связана с напряженностью электрического поля линейной зависимостью (закон Ома):
j =σE = ρ−1E = −ρ−1 U (r ) , |
(5.6) |
где σ и ρ - соответственно проводимость и удельное сопротивление
внеклеточной среды. В результате с учетом (5.5) статическое поле клетки во внеклеточной среде описывается уравнением Лапласа: ∆U = 0 .
Рис.5.2 Частотная зависимость импеданса мышечной ткани в двойном логарифмическом масштабе
Условия на внешней стороне мембраны этой клетки определяют однозначно разрешимую внешнюю краевую задачу. Ее решение является частным случаем формулы Кирхгоффа точно так же, как само уравнение Лапласа является частным случаем более общего уравнения Гельмгольца. Поэтому сразу пишем решение в виде
|
|
|
|
′ |
|
′ |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
U (r ) |
′ |
′ |
|
1 |
|
′ |
|
|
|||
|
|
|
|
|
|
|
|||||||||
U (r ) = − |
|
∫{ |
|
|
|
|
|
|
|
, |
(5.7) |
||||
|
|
−U (r ) ( |
′| |
)}ds |
|||||||||||
|
|
4π S |
| r |
− r ′| |
|
|
|
| r |
− r |
|
|
|
|||
где r - радиус-вектор точки наблюдения, |
|
r ′- |
радиус-вектор |
элемента |
|||||||||||
поверхности мембраны |
ds′. Здесь вектор нормали направлен из клетки, что |
||||||||||||||
привело к появлению общего знака минус. |
|
|
|
|
|
|
|
|
|||||||
Если считать мембрану |
бесконечно |
тонкой, |
то в соответствии с |
||||||||||||
непрерывностью нормальной компоненты плотности тока и законом Ома (5.6) нормальную производную от потенциала во внеклеточном пространстве можно связать с нормальной производной потенциала V внутри клетки
|
∂U |
|
|
|
|
|
ρ |
′ |
|
ρ |
|
′ |
|
ρ ∂V |
|
||||
En = − |
|
= ρjn |
= |
|
|
|
ρ jn = |
|
En = − |
|
|
|
, |
||||||
∂n |
ρ′ |
ρ′ |
ρ′ |
∂n |
|||||||||||||||
где ρ′- внутриклеточное удельное сопротивление. |
Тогда первое слагаемое в |
||||||||||||||||||
интегральном уравнении (5.6) равно. |
′ |
′ |
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
|
ρ |
|
|
|
|
|
|
|
|||||||
|
|
|
|
V (r ) |
|
|
|
|
|
|
|||||||||
|
|
− |
|
|
|
∫S |
| r |
− r ′| |
ds′. |
|
|
|
|
(5.8) |
|||||
|
|
4π |
|
ρ′ |
|
|
|
|
|||||||||||
Это выражение легко преобразовать к виду, аналогичному второму слагаемому в (5.6). Действительно, рассмотрим следующую разность интегралов
|
′V (r ′) |
′ ′ |
|
1 |
|
′ |
|
′ |
′V (r ′) |
′ ′ |
|
1 |
|
)}dv |
′ |
|
||||
∫{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.9) |
||||||
′| |
−V (r ) ( |
′| |
)}ds |
= ∫ { |
′| |
−V (r ) ( |
′| |
|
||||||||||||
S |
| r |
− r |
|
| r |
− r |
|
v |
|
| r |
− r |
|
| r |
− r |
|
|
|
||||
Здесь применена теорема Остроградского-Гаусса, в результате чего интегрирование производится по объему v внутри клетки. Производя дифференцирование в (5.9), нужно учесть, что внутри клетки источников тока также нет, поэтому внутриклеточный потенциал удовлетворяет уравнению Лапласа. Этому же уравнению удовлетворяет и статическая функция Грина −1
(4π | r − r ′|) , поэтому выражение (5.9) тождественно равно нулю при всех r
и произвольной форме поверхности клетки.
Подставляя теперь в уравнение (5.5) найденное значение интеграла (5.8), находим
|
|
1 |
|
|
|
ρ |
V |
′ |
|
′ |
′ |
|
1 |
|
|
|
′ |
|
|
|
U (r ) = − |
|
|
|
∫{ |
|
|
|
|
|
|
|
|
= |
(5.10) |
||||||
|
|
|
ρ′ |
(r ) −U (r )} ( |
|
|
′| |
)ds |
||||||||||||
|
|
4π S |
′ |
|
|
′ |
|
| r |
− r |
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
ρ |
r |
− r ′ |
|
|
′ |
|
|
|
|||||
= |
|
|
|
∫{U (r ) − |
|
V (r )} |
|
|
|
|
ds |
. |
|
|
||||||
|
|
|
ρ′ |
′| |
3 |
|
|
|||||||||||||
|
4π S |
|
|
|
|
| r − r |
|
|
|
|
|
|
|
|||||||
Этот красивый аналог основного интегрального решения (5.7) называется в честь автора формулой Плонзи и по сути связывает внеклеточные поля с мембранным потенциалом ϕ
U (r ′) − ρρ′V (r ′) = (1 − ρρ′)U (r ′) − ρρ′ϕ(r ′) .
В биологических тканях и в сером веществе мозга внутриклеточные потенциалы на один-два порядка превышают внеклеточные. Для серого
вещества мозга ρ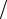
ρ′ ≈ 
10 ( ρ = 300 Ом·см), следовательно для оценок можно учитывать только слагаемое, пропорциональное ϕ . При ρ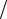
ρ′ =1 только это
слагаемое дает вклад в (5.10), а сама формула переходит в известную формулу потенциала двойного электрического слоя в однородной бесконечной среде.
Из вида выражения (5.10) следует, что главный вклад в поле вносят дипольные моменты. Это факт, известный еще из первых экспериментальных исследований внеклеточных полей. Для определения P используем формулу Плонзи. Согласно (7а) элемент мембраны характеризуется диполем
|
1 |
|
ρ |
|
|
dP = |
|
(U − |
|
V )ds . |
(5.11) |
4π |
ρ′ |
Для нейтральной совокупности зарядов полная величина диполя не зависит от выбора начала координат и есть сумма элементарных диполей
|
1 |
|
ρ |
|
|
P = |
|
∫(U − |
|
V )ds . |
(5.12) |
|
ρ′ |
||||
|
4π s |
|
|
||
Рассмотрим выражение (5.12) в применении к клетке-волокну. Учитывая, что в волокне потенциал меняется только в аксиальном направлении, разобьем интеграл (5.12) на две части. Первая часть учитывает особенности волокна: его дистальные концы, ветвления, в том числе тело клетки, изломы и резкие скачки сечения, иначе говоря, резкие изменения формы, около которых потенциал не успевает измениться (рис.5.3). Вторая часть интеграла соответствует отрезкам волокна между особенностями. Подынтегральное выражение первой части постоянно около каждой особенности, а интеграл поверхности мембраны заменим через противоположный ему вектор, образованный перпендикулярными сечениями, отделяющими особенность от остального волокна:
Рис.5.3 Особенности клетки-волокна I – ветвление; II – излом (угол); III – дистальный конец; 1 – 3 – номера веточек, причем одна и та же веточка может иметь разные номера для каждого из концов. Векторы – диполи веточек, выходящих из данной особенности
∫ds = −∑Sk ,a , |
|
s |
a |
где k - номер особенности, a - номер веточки волокна. Вектор Sk ,a направлен
от особенности вдоль a -й веточки волокна, исходящей от особенности. Отсюда
P1 = − |
1 |
∑(Uk − |
ρ |
Vk )∑Sk ,a . |
(5.13) |
|
4π |
ρ′ |
|||||
|
k |
a |
|
Для анализа второй части диполя волокна заменим интеграл по боковой поверхности малого цилиндра
∫ds = −∫dS dl s dl
векторами сечений, ограничивающих этот цилиндр. На отрезке постоянного
сечения и без искривлений оси P2 исчезает в общем случае: |
|
|||||
P2 = −∑ |
∫ |
(U − |
ρ |
V ) dS dl |
(5.14) |
|
ρ′ |
||||||
k ,a |
|
dl |
|
|||
Понятно, что при суммировании каждую ветвь необходимо учитывать только один раз. Если на некотором участке кабеля сечение меняется так быстро, что потенциалы можно считать постоянными, то интеграл (5.14) на этом участке есть выражение, идентичное (5.13), а сам этот участок можно включить в число особенностей.
Приведенные выражения представляют собой физическую основу для описания всех методов медицинской электрографии и, в частности, электроэнцефалографии (ЭЭГ). В этих методах регистрируются внеклеточные поля, возникающие при прохождении потенциалов действия в сером веществе мозга. В принципе выражения (5.10) – (5.14) дают возможность детального описания работы мозга по его зарегистрированной электрической активности, включая возможность пространственной локализации источников и характера активности в зависимости от состояния человека и вида его деятельности.
Дипольное представление о сердце лежит и в основе теории отведений Эйнтховена в электрокардиографии (ЭКГ). Согласно ей сердце обладает
дипольным моментом Pc , который поворачивается, изменяя свое положение и
точку приложения за время сердечного цикла. Для краткого описания теории отведений учтем, что расстояния от сердца до места наложения электродов много больше характерных размеров самого сердца, как источника поля и регистрируемых токов. Тогда формулу (5.10) с учетом выражения (5.11) можно записать в простом виде
U = ∫| rr −−rr′′|3 dP ≈ Pc rr3 .
На рис 5.4 показана идея отведений Эйнтховена, в соответствии с которой напряжения в отведениях I, II и III соотносятся точно так же, как проекции дипольного момента сердца на стороны равностороннего треугольника. Это дает возможность не только регистрировать зависимость напряжения от