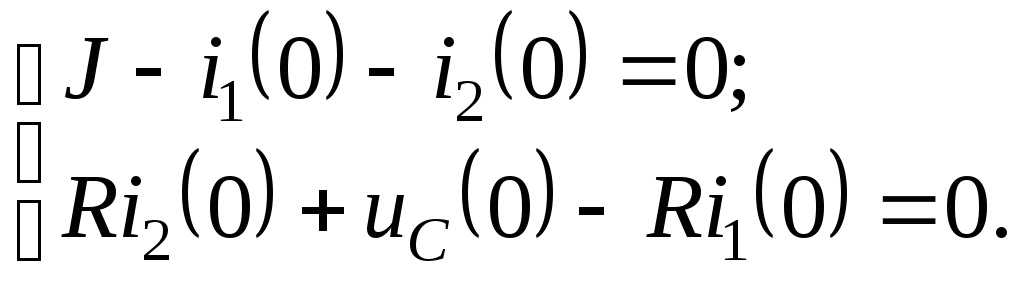- •Министерство образования и науки Российской Федерации
- •Введение
- •Перечень условных обозначений
- •1 Основные теоретические положения
- •1.1. Физические основы переходных процессов
- •1.2 Математический аппарат и алгоритмы расчетов
- •1.2.1 Классический метод анализа переходного процесса
- •1.2.2 Операторный метод расчета (метод преобразования Лапласа)
- •1.2.3 Расчет методом интеграла Дюамеля
- •1.2.4 Метод переменных состояния переходных процессов
- •2 Классический метод расчета переходных процессов в линейных электрических цепях
- •2.1 Примеры расчета переходных процессов в цепях с индуктивностью
- •Имеет один отрицательный и действительный корень
- •Решение
- •И подставим его в первое уравнение системы:
- •Источника напряжения
- •Получим характеристическое уравнение
- •Решение
- •Первый способ
- •Решение
- •Ом; Ом.
- •Решение
- •Решение
- •И падение напряжение на индуктивности
- •Решение
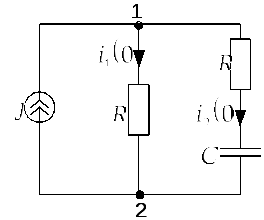
- •Поэтому в соответствии с первым законом Кирхгофа для узла “1” ток в индуктивности, питаемый источником тока равен току в ветви с резистором: а.
- •Откуда составляем характеристическое уравнение:
- •Где ток в конденсаторе.
- •Отсюда находим характеристическое уравнение:
- •С-1; с-1.
- •С-1; с-1.
- •Решение
- •Напряжение между узлами 1 и 2 определяется как:
- •И подставим туда ток конденсатора (2.6.6):
- •Откуда характеристическое уравнение оду будет иметь вид:
- •2.8 Задачи для самостоятельного решения
- •3 Операторный метод расчета переходных процессов в линейных электрических цепях
- •3.1 Примеры расчета переходных процессов в цепях постоянного тока
- •Решение
- •Решение
- •3.2 Примеры расчета переходных процессов в цепях переменного тока
- •С-1; с-1;
- •По закону Ома для участка цепи определяем искомый операторный ток:
- •С-1; с-1;
- •4 Расчет переходных процессов с помощью интеграла дюамеля
- •4.1 Примеры расчета переходных и импульсных характеристик
- •Тогда по закону Ома в операторной форме определяем ток
- •Решение
- •С-1; с-1;
- •4.2 Примеры расчета переходных процессов с помощью интеграла Дюамеля
- •Решение
- •4.3 Задачи для самостоятельного решения
- •5 Расчет переходных процессов методом переменных состояния
- •5.1 Примеры расчета
- •Определим собственные значения матрицы a, т.Е. Корни уравнения
- •. Определим собственные значения матрицы a, т.Е. Корни уравнения
- •5.2 Задачи для самостоятельного решения
- •Список литературы
- •Содержание
- •Часть II
- •190008, Г.С.-Петербург, ул. Лоцманская, 3.
Получим характеристическое уравнение
![]()
которое имеет один отрицательный, вещественный корень
![]() с-1.
с-1.
Поэтому решение приведенного НДУ имеет вид:
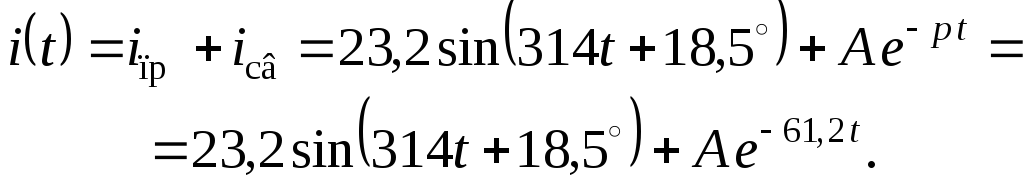
Постоянную интегрирования
![]() найдем используя начальные условия:
найдем используя начальные условия:
![]()
где
![]() ток в момент замыкания ключа К, который
по первому закону коммутации равен току
в цепи до коммутации:
ток в момент замыкания ключа К, который
по первому закону коммутации равен току
в цепи до коммутации:
![]()
Тогда
![]()
Таким образом, переходной ток в индуктивности
![]() А.
А.
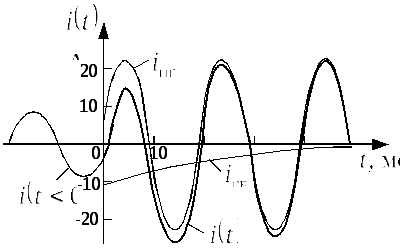
График тока приведен на рис. 2.1.7.г.
|
|
|
Рис. 2.1.7.г |
2.2 Примеры расчета переходных процессов в цепях с емкостью
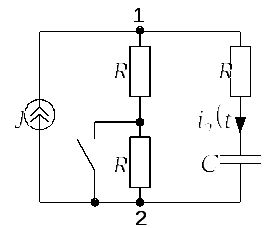
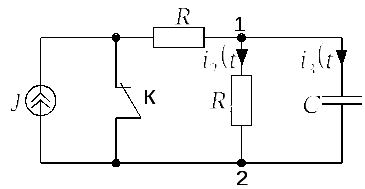
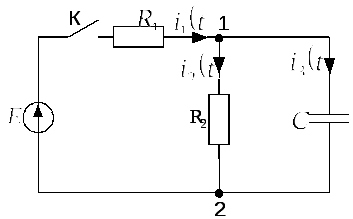
Задача 2.2.1Источник тока создает в
цепи, представленной на рис. 2.2.1.а ток![]() А. В момент времени
А. В момент времени![]() ключ К шунтирует резистор с сопротивлением
ключ К шунтирует резистор с сопротивлением![]() Ом. Определить ток
Ом. Определить ток![]() в этот момент времени.
в этот момент времени.
|
|
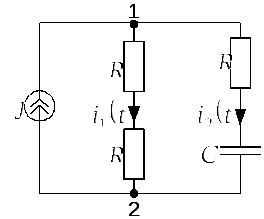
Решение 1) На
рис. 2.2.1.б приведена схема до коммутации
По
закону Ома определим напряжение на
емкости
2) В
момент коммутации, т.е. при
Для
определения тока в момент коммутации
Из
первого уравнения системы выразим
ток
и подставим во второе уравнение:
откуда искомый ток
т.е. его истинное направление противоположно выбранному. |
|
Рис. 2.2.1.а | |
|
| |
|
Рис. 2.2.1.б | |
|
| |
|
Рис. 2.2.1.в |
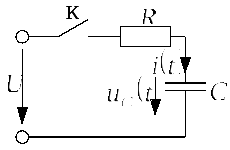
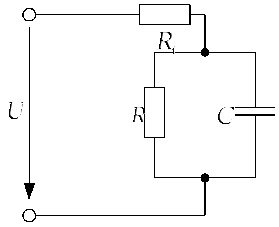
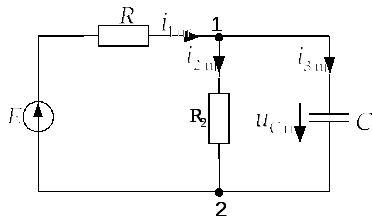
Задача 2.2.2 На рис. 2.2.2.а представлена
простейшая![]() цепь с параметрами:
цепь с параметрами:![]() Ом,
Ом,![]() мкФ. В момент
мкФ. В момент![]() в цепи происходит коммутация – замыкание
ключа К, в результате чего в цепь
подключается источник постоянного
напряжения
в цепи происходит коммутация – замыкание
ключа К, в результате чего в цепь
подключается источник постоянного
напряжения![]() В. Найти законы изменения в функции
времени следующих физических величин:
напряжения между обкладками конденсатора
В. Найти законы изменения в функции
времени следующих физических величин:
напряжения между обкладками конденсатора![]() тока в конденсаторе
тока в конденсаторе![]() и падения напряжения на резисторе
и падения напряжения на резисторе![]()
|
|
Решение 1) До
коммутации
2) Схема после
коммутации
|
|
Рис. 2.2.а |
|
|
Это значит, что конденсатор разрывает цепь протекания тока и поэтому
Тогда из уравнения, составленного по второму закону Кирхгофа
|
|
Рис. 2.2.б |
ввиду равенства нулю слагаемого
![]() следует, что напряжение между обкладками
конденсатора уравновешивается постоянным
напряжением
следует, что напряжение между обкладками
конденсатора уравновешивается постоянным
напряжением![]() :
:
![]()
То есть конденсатор в установившемся
режиме работы цепи после коммутации
заряжен до напряжения источника
![]()
3) С целью расчета переходного процесса
для схемы, изображенной на рис. 2.2.а, в
момент коммутации
![]() при замкнутом ключе К составляем исходное
уравнение по второму закону Кирхгофа:
при замкнутом ключе К составляем исходное
уравнение по второму закону Кирхгофа:
![]()
Решим это уравнение относительно
напряжения
![]() Для этого воспользуемся формулой,
связывающую мгновенные значения тока
и напряжения конденсатора:
Для этого воспользуемся формулой,
связывающую мгновенные значения тока
и напряжения конденсатора:
![]()
Тогда исходное уравнение можно записать иначе:
|
|
(2.2.1) |
Последнее уравнение является НДУ первого
порядка, разрешенного относительно
напряжения
![]() Приравняв правую часть НДУ (2.2.1) к нулю
Приравняв правую часть НДУ (2.2.1) к нулю![]() получим ОДУ первого порядка:
получим ОДУ первого порядка:
![]()
Из ОДУ составим характеристическое
уравнение с помощью известных правил
математики (заменив производную
![]() переменной
переменной![]() и неизвестную величину
и неизвестную величину![]() единицей):
единицей):
![]()
Отсюда находим корень характеристического уравнения:
![]() с-1.
с-1.
Характеристическое уравнение имеет один вещественный и отрицательный корень, поэтому в цепи будет наблюдаться апериодический переходной процесс первого порядка.
Общее решение НДУ (2.2.1) для напряжения
![]() представим как принужденного напряжения
представим как принужденного напряжения![]()
![]()
Здесь
![]() – принужденная составляющая напряжения
(это частное решение НДУ), определенная
в пункте 2,
– принужденная составляющая напряжения
(это частное решение НДУ), определенная
в пункте 2,
![]() В;
В;
![]() – свободная составляющая (это общее
решение ОДУ), выражение для которой при
одном отрицательном и вещественном
корне характеристического уравнения
представляется в виде:
– свободная составляющая (это общее
решение ОДУ), выражение для которой при
одном отрицательном и вещественном
корне характеристического уравнения
представляется в виде:
![]()
Тогда окончательно запишем общее решение НДУ (2.2.1):
![]()
Для нахождения постоянной интегрирования
![]() подставим в последнее выражение время
подставим в последнее выражение время![]()
![]()
где
![]() – напряжение на конденсаторе в момент
замыкания ключа К, которое в соответствии
со вторым законом коммутации в момент
начала переходного процесса не должно
измениться скачком и поэтому должно
быть равно напряжению при
– напряжение на конденсаторе в момент
замыкания ключа К, которое в соответствии
со вторым законом коммутации в момент
начала переходного процесса не должно
измениться скачком и поэтому должно
быть равно напряжению при![]()
![]()
Тогда имеем:
![]()
откуда
![]()
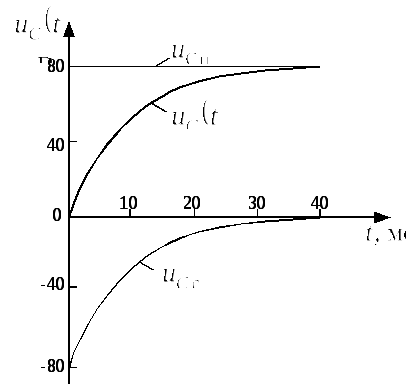
Таким образом, закон изменения напряжения на конденсаторе в функции времени имеет вид:
![]() В.
В.
Рассчитаем с помощью приведенного выше соотношения ток в цепи:
![]() А.
А.
По закону Ома определяем падение
напряжения на резисторе
![]()
![]() В.
В.
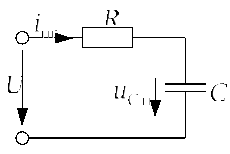
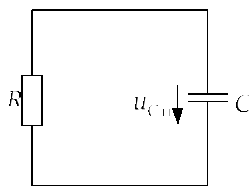
Задача 2.2.2Конденсатор с утечкой,
параметры которого![]() мкФ,
мкФ,![]() кОм в момент
кОм в момент![]() при размыкании ключа К отключается от
источника постоянного напряжения
при размыкании ключа К отключается от
источника постоянного напряжения![]() В. Определить напряжение на конденсаторе
через
В. Определить напряжение на конденсаторе
через![]() мс после выключения в схеме, изображенной
на рис. 4.2.2.а. Внутренним сопротивлением
источника напряжения
мс после выключения в схеме, изображенной
на рис. 4.2.2.а. Внутренним сопротивлением
источника напряжения![]() пренебречь.
пренебречь.
|
|
|
|
|
Рис. 2.2.2.а |
Рис. 2.2.2.б |
Рис.2.2.2.в |
1) Цепь, соответствующая установившемуся
режиму работу цепи до коммутации
![]() приведена на рис. 2.2.2.б. Конденсатор
полностью заряжен до напряжения источника
питания:
приведена на рис. 2.2.2.б. Конденсатор
полностью заряжен до напряжения источника
питания:
![]() В.
В.
2) Послекоммутационная схема
![]() дана на рис. 4.2.2.в. В установившемся
режиме конденсатор полностью разрядиться
через резистор
дана на рис. 4.2.2.в. В установившемся
режиме конденсатор полностью разрядиться
через резистор![]() поэтому напряжение емкостном элементе
поэтому напряжение емкостном элементе
![]()
3) Для расчета переходного процесса в
схеме, представленной на рис. 22.2.а, в
момент коммутации
![]() при замыкании ключа К составим уравнение
по второму закону Кирхгофа для замкнутого
при замыкании ключа К составим уравнение
по второму закону Кирхгофа для замкнутого![]() контура:
контура:
![]()
Т.к. ток в конденсаторе
![]() то
последнее уравнение примет следующий
вид:
то
последнее уравнение примет следующий
вид:
![]()
Это уравнение является НДУ первого порядка, которое в силу равенства нулю правой части совпадает с ОДУ
![]()
Характеристическое уравнение
![]()
имеет один отрицательный действительный корень
![]() с-1.
с-1.
Поэтому общее решение НДУ представиться в виде:
![]()
Постоянную интегрирования
![]() определим, используя начальные условия.
Для этого запишем последнее выражение
при
определим, используя начальные условия.
Для этого запишем последнее выражение
при![]()
![]()
Учтем, что в соответствии со вторым законом коммутации напряжение на конденсаторе не может изменяться скачком, поэтому
![]()
Тогда
![]()
Итак, напряжение на конденсаторе
![]() В.
В.
4) Определим напряжение на конденсаторе
через
![]() мс
после выключения путем подстановки в
последние выражение
мс
после выключения путем подстановки в
последние выражение![]() с:
с:
![]() В.
В.
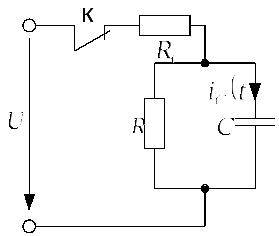
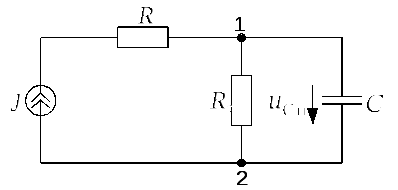
Задача 2.2.3Цепь, представленная на
рис. 2.2.3.а, в момент![]() при размыкании ключа К включается под
действие источника постоянного тока
при размыкании ключа К включается под
действие источника постоянного тока![]() А. Определить напряжение на конденсаторе
в функции времени и построить его график,
если
А. Определить напряжение на конденсаторе
в функции времени и построить его график,
если![]() Ом,
Ом,![]() Ом,
Ом,![]() мкФ.
мкФ.
|
|
Решение 1) До
коммутации
2)
Схема после коммутации
3) Для расчета переходного процесса в послекоммутационной схеме составим для |
|
Рис. 2.2.3.а | |
|
| |
|
Рис. 2.2.3.б |
контура, не содержащего источника тока:
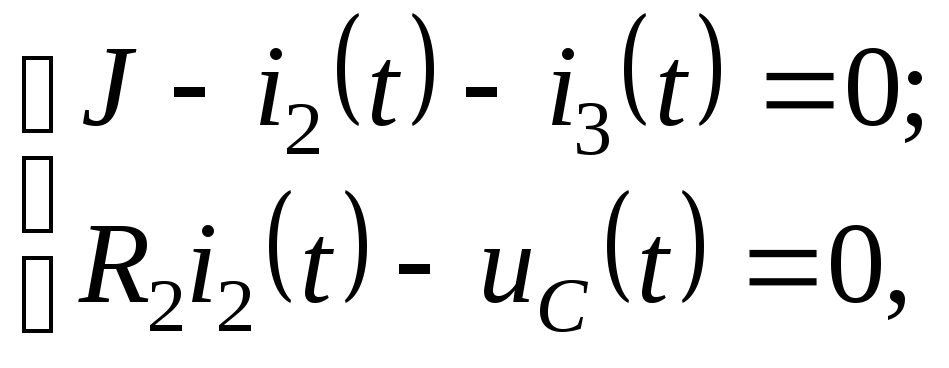
где
![]() ток
в конденсаторе.
ток
в конденсаторе.
Решим ее относительно напряжения
![]() способом подстановки. Для этого из
второго уравнения системы выразим ток
во второй ветви
способом подстановки. Для этого из
второго уравнения системы выразим ток
во второй ветви
![]()
и подставим его, а также ток
![]() в первое уравнение исходной системы:
в первое уравнение исходной системы:
![]()
После простых преобразований получим искомое НДУ первого порядка:
![]()
Приравняв правую часть этого уравнения
к нулю:
![]() т.е. освободив цепь от действия вынуждающей
силы в виде источника тока, получим ОДУ
первого порядка:
т.е. освободив цепь от действия вынуждающей
силы в виде источника тока, получим ОДУ
первого порядка:
![]()
Характеристическое уравнение имеет вид:
![]()
Его корень
![]() с-1.
с-1.
получается единственным, вещественным и отрицательным, в силу чего общее решение НДУ примет следующий вид:
![]() В.
В.
Постоянную интегрирования
![]() определим, используя начальные условия:
определим, используя начальные условия:
![]()
|
|
где
Таким образом, напряжение на конденсаторе определяется выражением:
График напряжения построен на рис. 4.2.3.в.
|
|
Рис. 2.2.4.в |
Задача 2.2.4Цепь, представленная на
рис. 2.2.4.а, в момент![]() замыкается ключом К к источнику постоянной
ЭДС
замыкается ключом К к источнику постоянной
ЭДС![]() В. Найти все токи и напряжение
В. Найти все токи и напряжение![]() на емкости. Параметры цепи:
на емкости. Параметры цепи:![]() Ом,
Ом,![]() Ом,
Ом,![]() пФ.
пФ.
|
|
|
|
Рис. 2.2.4.а |
Рис. 2.2.4.б |