С-1; с-1.

5) Определение постоянных интегрирования. Так характеристическое уравнение имеет один отрицательный корень и два комплексно – сопряженных то выражение для тока представим в следующем виде:

(2.5.17)

Постоянные интегрирования и найдем следующим образом.

Найдем первую и вторую производную от выражения (2.5.17) по и составим систему из этих двух уравнений а также из уравнения (2.5.17), записанных при Тогда используя начальные условия мы получим замкнутую систему из трех уравнений для определения трех неизвестных – и . И тогда из этой системы можно найти постоянные интегрирования, а значит и выражение для переходного тока .

Согласно намеченному плану определим первую производную по от выражения (2.5.17):

Продифференцируем (2.5.18) по

Теперь перепишем (4.5.17) и два последних уравнения при В результате получим следующую систему уравнений:

(2.5.18)

В системе уравнений (2.5.18) можно определить зависимые начальные условия – и через ранее найденные независимые начальные условия.

Запишем уравнение (2.5.5) при

откуда определяем первую производную от тока в индуктивности в момент коммутации

А/с.

Для определения второй производной перепишем уравнение (2.5.5) следующим образом:

Теперь продифференцируем левую и правую части данного выражения по

при имеем:

(2.5.19)

Здесь можно легко определить токи и из уравнений (2.5.9) и (2.5.10), записанных при

Тогда уравнение (2.5.19) преобразуется к виду:

поэтому вторая производная

Подставив теперь значения тока , а также его производных и в систему (4.5.18) и сделав группировку слагаемых, окончательно получим:

	(2.5.20)
	(2.5.21)
	(2.5.22)

где

Умножим левую и правую части уравнения (2.5.22) на множитель Тогда получим:

(2.5.23)

Сложим почленно уравнение (2.5.21) с уравнением (2.5.23):

После упрощений получаем:

(2.5.24)

где

Выразим из уравнения (2.5.20)

(2.5.25)

Подставим (2.5.25) в выражение (2.5.24):

откуда определяем постоянную интегрирования

Подставив (4.5.25) в уравнение (4.5.21), находим

Тогда по формуле (4.5.25) определим

Зная все постоянные интегрирования, окончательно запишем закон изменения переходного тока в катушке индуктивности:

А.

Проверим первый закон коммутации, подставив в последнее выражение для тока

Тождество выполняется, что говорит о правильности определения данного тока.

Задача 2.5.2 Цепь, представленная на рис. 2.5.2.а, запитывается от источника постоянного напряжения с ЭДС В. В момент происходит подключение ветви с индуктивностью к цепи. Известны следующие параметры цепи: мГн, мГн, мкФ, Ом, Ом. Определить выражения для вех токов и напряжения между обкладками конденсатора

Рис. 2.5.2.а	Рис. 2.5.2.б

Решение

1) Схема до коммутации приведена на рис. 2.5.2.б. Ток в катушке с индуктивностью равен току заряженного до напряжения источника ЭДС конденсатора т.е.:

В.

Пи этом тока в катушке с индуктивностью нет:

Тогда используя первые и вторые законы коммутации, получаем следующие независимые начальные условия:

В.

	2) Схема после коммутации вычерчена на рис. 2.5.2.в. Падение напряжения от постоянного тока на катушке с индуктивностью Составим уравнение по второму закону Кирхгофа для замкнутого контура
Рис. 2.5.2.в

Учтем, что ток в заряженном до установившегося (т.е. неизменного во времени) напряжения равен нулю:

Тогда падение напряжения на резисторе в предпоследнем уравнении равно нулю, и, следовательно,

Запишем уравнение по второму закону Кирхгофа для внешнего контура:

Так как и то

откуда

А.

По первому закону Кирхгофа, составленного для узла “1”, следует, что

А.

3) Для послекоммутационной схемы (ключ К замкнут) составляем исходную систему из трех уравнений: первое – по первому закону Кирхгофа для узла “1”, второе – по второму закону Кирхгофа для контура третье – по второму закону Кирхгофа для контура

(2.5.26)

где – ток, протекающий через конденсатор с емкостью С и резистор

(2.5.27)

Решим систему (2.5.26) относительно напряжения между обкладками конденсатора способом подстановки.

Подставим в третье уравнение системы (2.5.26) ток (2.5.27):

Выразим из последнего выражения ток в функции напряжения

(2.5.28)

иначе:

Проинтегрировав правую и левые части последнего соотношения, получаем:

Подставим последнее выражение и соотношение (2.5.27) в первое уравнение системы (2.5.26):

Теперь сделаем подстановку двух последних выражений и тока по выражению (2.5.27) во второе уравнение системы (2.5.26):

Дважды продифференцировав это уравнение, сделав ряд упрощений, получаем НДУ третьего порядка:

Из этого НДУ составим ОДУ третьего порядка:

Из приведенного ОДУ получаем характеристическое уравнение:

Определяем с помощью ЭВМ (например, персональный компьютер, программа “Маткад”) корни кубического уравнения:

с^-1;

Общее решение составленного выше НДУ в случае одного отрицательного вещественного корня и двух комплексно – сопряженных корня представим в виде:

Для определения постоянных интегрирования найдем первую и вторую производные от последнего выражения:

Составим систему уравнений из трех последних уравнений при

(2.5.29)

Определим два неизвестных начальных условия: и

Подставим формулу (2.5.27) в первое уравнение системы (4.5.26):

(2.5.30)

В частности, для момента

Так как и значит

следовательно,

Теперь для нахождения значения продифференцируем по уравнение (2.5.30):

(2.5.31)

При уравнение (2.5.31) приобретает вид:

(2.5.32)

Из второго уравнения системы (2.5.26), записанного при можно сразу определить

Определим значение из третьего уравнения системы (2.5.26), составленного при

А/с.

Здесь в соответствии со вторым законом Кирхгофа ток

Тогда из формулы (2.5.32) определяем

В²/С².

Тогда система уравнений (2.5.29) преобразуется к виду:

(2.5.33)

Отсюда найдем три неизвестных постоянных интегрирования.

Из первого уравнения системы (2.5.33) выразими подставим во второе уравнение:

Откуда

(2.5.34)

Исключим из третьего уравнения системы (2.5.33) и путем их подстановки:

Подставим (2.5.34) в последнее уравнение:

Из этого уравнения определяем

Тогда согласно формуле (4.5.33)

Теперь определим

Итак, запишем выражение для напряжения между обкладками конденсатора:

В.

По выражению (4.5.27) определим ток в конденсаторе:

А.

Запишем общее решение для тока

.

Постоянные интегрирования определим аналогично предыдущему случаю: составим систему из трех уравнений, записанных для

Здесь начальное условие определим дифференцирования по ранее составленного уравнения (2.5.28):

При получаем:

А²/с².

Тогда последняя система уравнений преобразуется к виду:

Постоянные интегрирования:

выраженные из первого второго уравнения последней системы подставим в третье уравнение этой же системы:

Отсюда определяем

Тогда:

Окончательно получаем:

А.

В соответствии с первым уравнением системы (4.5.26) определяем ток во входной ветви:

А.

Окончательно запишем полученные искомые временные функции:

А;

А;

А;

В.

2.6 Примеры расчета переходных процессов при наличии двух источников энергии

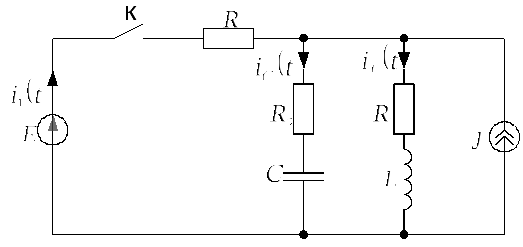
Задача 2.6.1В цепи, изображенной на рис. 4.4.1.а., размыкается ключ К в ветви с резистором Определить токи во второй и третьей ветвях схемы, если: В, А, Ом, Гн. Построить графики этих токов.

Рис. 2.6.1.а	Рис. 2.6.1.б

Решение

1) Составляем (вычерчиваем) схему исходной цепи. Схема при представлена на рис. 4.4.1.б. Определим ток в индуктивности, используя, например, метод двух узлов. Для этого найдем напряжение между узлами 1 и 2 –

В,

тогда ток в катушке индуктивности (в третьей ветви)

А.

	2) Вычерчиваем цепь для установившегося режима. Схема для изображена на рис.2.6.1.в. Для определения тока запишем уравнение, составленное по второму закону Кирхгофа для контура не содержащего источника тока и подставим в него ток выраженный из уравнения, составленного по первому закону Кирхгофа для узла “1”:
Рис. 2.6.1.в

откуда

А.

3) Для расчета переходного процесса в схеме, представленной на рис. 2.6.1.а, в момент коммутации при размыкании ключа К составим систему дифференциальных уравнений:

Решим систему относительно тока протекающего в катушке индуктивности, так как для нее выполняется первый закон коммутации ­– запрет скачка тока в индуктивности. Для этого из первого уравнения системы найдем ток

и подставим его во второе уравнение системы:

После группировки слагаемых получим искомое НДУ первого порядка:

Приравнивая правую часть последнего уравнения к нулю, получим ОДУ:

откуда получаем характеристическое уравнение

Корень характеристического уравнения

с^-1

получается единственным, вещественным, отрицательным, следовательно решение ОДУ имеет вид

Полное решение НДУ запишем в виде:

Постоянную интегрирования найдем, используя начальные условия. Для этого запишем последнее уравнение при

Учтем, что в соответствии с первым законом коммутации ток в индуктивности не может измениться скачком и должен быть равен току при Получим

А.

Тогда

Таким образом, закон изменения тока в цепи с катушкой индуктивности:

А.

Применяя первый закон Кирхгофа для узла 1 найдем ток :

А.

Графики токов приведены на рис. 2.6.1.г.

Рис. 2.6.1.г

Задача 2.6.2В цепи, представленной на рис. 2.6.2.а, замыкается ключ К в первой ветви. Определить токи и напряжение , если В, А, Ом, мкФ, Гн.

Решение

1) Для момента времени схема изображена на рис. 2.6.2.б. Так как конденсатор отрывает цепь после заряда то ток в индуктивности будет равен току источника А, а ток в конденсаторе Напряжение на конденсаторе будет равно напряжению между узлами 1 и 2 или падению напряжения на резисторе так как на постоянном токе индуктивное сопротивление у катушки отсутствует

Рис. 2.6.2.а	Рис.2.6.2.б
	2) Расчет установившегося режима после коммутации . Схема, соответствующая установившемуся режиму (при ) представлена на рис. 2.6.2.в. Постоянный ток в конденсаторе не течет, следовательно Согласно методу двух узлов
Рис. 2.6.2.в