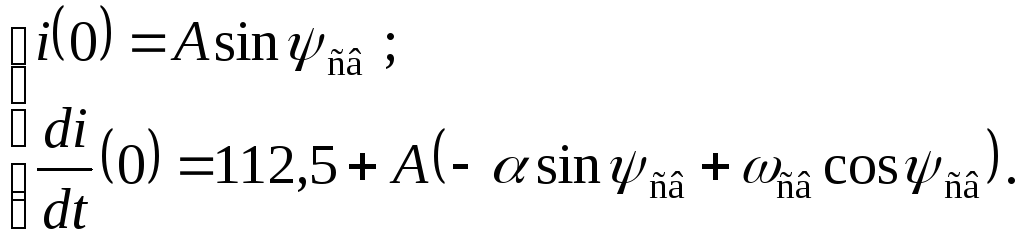- •Министерство образования и науки Российской Федерации
- •Введение
- •Перечень условных обозначений
- •1 Основные теоретические положения
- •1.1. Физические основы переходных процессов
- •1.2 Математический аппарат и алгоритмы расчетов
- •1.2.1 Классический метод анализа переходного процесса
- •1.2.2 Операторный метод расчета (метод преобразования Лапласа)
- •1.2.3 Расчет методом интеграла Дюамеля
- •1.2.4 Метод переменных состояния переходных процессов
- •2 Классический метод расчета переходных процессов в линейных электрических цепях
- •2.1 Примеры расчета переходных процессов в цепях с индуктивностью
- •Имеет один отрицательный и действительный корень
- •Решение
- •И подставим его в первое уравнение системы:
- •Источника напряжения
- •Получим характеристическое уравнение
- •Решение
- •Первый способ
- •Решение
- •Ом; Ом.
- •Решение
- •Решение
- •И падение напряжение на индуктивности
- •Решение
- •Поэтому в соответствии с первым законом Кирхгофа для узла “1” ток в индуктивности, питаемый источником тока равен току в ветви с резистором: а.
- •Откуда составляем характеристическое уравнение:
- •Где ток в конденсаторе.
- •Отсюда находим характеристическое уравнение:
- •С-1; с-1.
- •С-1; с-1.
- •Решение
- •Напряжение между узлами 1 и 2 определяется как:
- •И подставим туда ток конденсатора (2.6.6):
- •Откуда характеристическое уравнение оду будет иметь вид:
- •2.8 Задачи для самостоятельного решения
- •3 Операторный метод расчета переходных процессов в линейных электрических цепях
- •3.1 Примеры расчета переходных процессов в цепях постоянного тока
- •Решение
- •Решение
- •3.2 Примеры расчета переходных процессов в цепях переменного тока
- •С-1; с-1;
- •По закону Ома для участка цепи определяем искомый операторный ток:
- •С-1; с-1;
- •4 Расчет переходных процессов с помощью интеграла дюамеля
- •4.1 Примеры расчета переходных и импульсных характеристик
- •Тогда по закону Ома в операторной форме определяем ток
- •Решение
- •С-1; с-1;
- •4.2 Примеры расчета переходных процессов с помощью интеграла Дюамеля
- •Решение
- •4.3 Задачи для самостоятельного решения
- •5 Расчет переходных процессов методом переменных состояния
- •5.1 Примеры расчета
- •Определим собственные значения матрицы a, т.Е. Корни уравнения
- •. Определим собственные значения матрицы a, т.Е. Корни уравнения
- •5.2 Задачи для самостоятельного решения
- •Список литературы
- •Содержание
- •Часть II
- •190008, Г.С.-Петербург, ул. Лоцманская, 3.
Отсюда находим характеристическое уравнение:
![]()
![]()
![]()
Определим корни последнего уравнения:
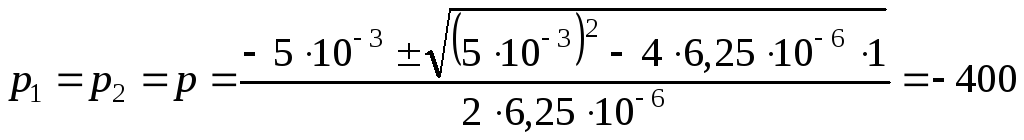 с-1.
с-1.
Так как корни характеристического уравнения получились кратными, отрицательными и действительными, то общее решение ОДУ будет иметь вид:
|
|
(2.3.15) |
Постоянные интегрирования найдем следующим образом. Запишем ток в конденсаторе через его напряжение по выражению (2.3.15):
![]()
Составим систему из выражения (2.3.15) и последнего уравнения:

При
![]() получаем:
получаем:

Здесь в соответствии с законами коммутации можно записать:
![]()
![]() А.
А.
Тогда получаем систему уравнений:
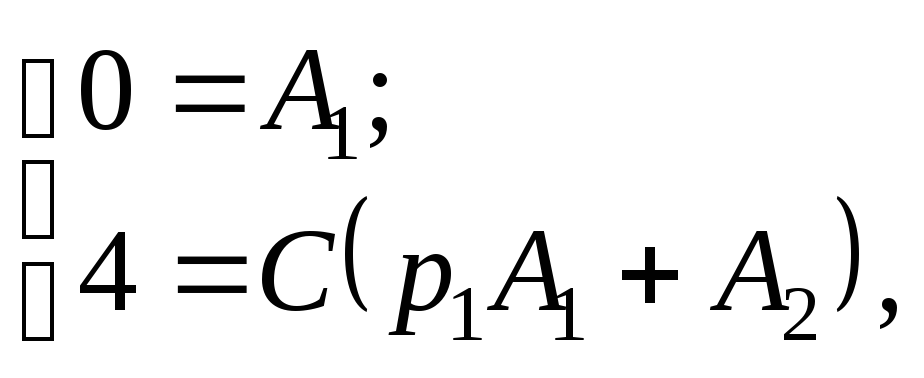
из которой следует что
![]()
![]()
Таким образом, напряжение на конденсаторе
![]() В,
В,
а ток в цепи
![]()
![]() А.
А.
Задача 2.3.11 В цепи, изображенной на
рис. 2.3.11.а действует источник синусоидальной
ЭДС![]() с амплитудой
с амплитудой![]() В и угловой частотой
В и угловой частотой![]() с-1. В момент
с-1. В момент![]() происходит подключение к цепи ветви с
резистором
происходит подключение к цепи ветви с
резистором![]() Определить закон изменения тока
Определить закон изменения тока![]() Параметры цепи:
Параметры цепи:![]() Ом,
Ом,![]() Ом,
Ом,![]() Гн,
Гн,![]() мкФ.
мкФ.
|
|
|
|
Рис. 2.3.11.а |
Рис. 2.3.11.б |
Решение
Для определения установившихся состояний цепи рассчитаем реактивные сопротивления:
![]() Ом;
Ом;
![]() Ом.
Ом.
1) Схема до коммутации
![]() приведена на рис. 2.3.11.б. Расчет произведем
символическим методом. Сначала найдем
эквивалентное комплексное сопротивлении
цепи
приведена на рис. 2.3.11.б. Расчет произведем
символическим методом. Сначала найдем
эквивалентное комплексное сопротивлении
цепи![]()
![]() Ом.
Ом.
В этой цепи наблюдается резонанс токов.
Тогда по закону Ома комплекс тока на входе цепи
![]() А.
А.
Методом “чужой ветви” определим комплекс тока в катушке:
![]() А.
А.
По закону Ома определяем напряжение в емкости:
![]() В.
В.
Прейдем от комплексных изображений к их мгновенным значениям:
![]() А;
А;
![]() В.
В.
2) Послекоммутационная схема вычерчена на рис. 4.3.15.в. Расчет схемы произведем символическим методом.
Определим эквивалентное комплексное
сопротивлении цепи
![]()

 Ом.
Ом.
Здесь также наблюдается режим резонанса токов.
Определим комплекс входного тока:
|
|
Тогда его временная функция представиться в следующем виде:
3)
Расчет цепи в момент коммутации.
Используя схему, представленную на
рис. 2.3.11.а, составим исходную систему
уравнений на основании первого и
второго законов Кирхгофа для нахождения
переходного тока
| |
|
Рис. 2.3.11.в | ||
|
|
(2.3.16) | |
|
(2.3.17) | ||
|
(2.3.18) | ||
|
(2.3.19) | ||
где
![]()
Из уравнения (2.3.17) выразим
ток![]()
|
|
(2.3.20) |
Для того чтобы избавиться от интеграла
в уравнении (2.3.18) продифференцируем по
времени
![]() его правую и левую части:
его правую и левую части:
![]()
откуда
|
|
(2.3.21) |
Подставим выражения (2.3.19) и (2.3.20) в уравнение (2.3.16):
![]()
Тогда
|
|
(2.3.22) |
Подставим (2.3.22) в уравнение (2.3.18):


![]()
После упрощений получаем НДУ второго
порядка относительно тока
![]()
![]()
![]()
Приравняв правую часть этого уравнения к нулю, получаем ОДУ второго порядка:
![]()
Тогда имеем следующее характеристическое уравнение:
![]()
![]()
![]()
Определим его корни:
![]() с-1.
с-1.
Так как корни характеристического уравнения получаются комплексно –сопряженными, то общее решение НДУ представим в виде:
|
|
(2.3.23) |
Постоянные интегрирования определим следующим образом.
Продифференцируем НДУ (2.3.23)
по![]()

Составим систему из выражения (2.3.23) и последнего уравнения:

При
![]() получаем:
получаем:
|
|
(2.3.24) |
Здесь можно найти зависимые начальные
условия
![]() и
и![]() через независимые начальные условия.
Используя закону коммутации запишем
независимые начальные условия:
через независимые начальные условия.
Используя закону коммутации запишем
независимые начальные условия:
![]() А;
А;
![]()
Для определения тока
![]() запишем уравнение (4) при
запишем уравнение (4) при![]()
![]()
где
![]()
Тогда
![]()
Для определения производной от тока
![]() в момент коммутации –
в момент коммутации –![]() перепишем уравнение (2.3.21) следующим
образом:
перепишем уравнение (2.3.21) следующим
образом:
![]()
где
![]() В/с.
В/с.
Тогда производная
тока
![]()
![]()
При
![]() можно записать:
можно записать:
![]()
Здесь
![]() В/с. Найдем ток в конденсаторе
В/с. Найдем ток в конденсаторе![]() .
.
Из уравнения (2.3.17), записанного при
![]()
![]()
находим ток
![]()
Из (2.3.16) при
![]() имеем:
имеем:
![]()
или
![]()
Следовательно,
![]() А.
А.
Окончательно получаем:
![]() А/с.
А/с.
Тогда система уравнений (2.3.24) предстанет в виде:

Так как левая часть второго уравнения
не может быть равно нулю, значит
![]() и из первого уравнения следует, что
и из первого уравнения следует, что![]() Тогда получаем постоянные интегрирования:
Тогда получаем постоянные интегрирования:
![]()
![]()
Итак,
![]() А.
А.
Задача 4.3.12 Цепь, изображенная на
рис. 2.3.12.а, питается от источника
переменного напряжения промышленной
частоты с ЭДС![]() В. В момент
В. В момент![]() происходит переключение ключа К с
положения “1” в положение “2”. Найти
выражения для тока в индуктивном элементе
происходит переключение ключа К с
положения “1” в положение “2”. Найти
выражения для тока в индуктивном элементе![]() и напряжения между обкладками конденсатора
и напряжения между обкладками конденсатора![]() если известны следующие параметры цепи:
если известны следующие параметры цепи:![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом,
Ом,![]() мГн,
мГн,![]() мкФ.
мкФ.
|
|
|
|
Рис. 2.3.12.а |
Рис. 2.3.12.б |
Решение
Определим реактивные сопротивления индуктивного и емкостного элементов:
![]() Ом;
Ом;
![]() Ом.
Ом.
1) До коммутации
![]() схема изображена на рис. 2.3.12.б. Здесь
ветвь с резистором
схема изображена на рис. 2.3.12.б. Здесь
ветвь с резистором![]() отключена. Найдем эквивалентное
сопротивление цепи:
отключена. Найдем эквивалентное
сопротивление цепи:
![]() Ом.
Ом.
По закону Ома определяем комплекс
входного тока
![]()
 А,
А,
т.е. здесь имеет место совпадения фазы входного тока и ЭДС – резонанс напряжений.
Напряжение на конденсаторе здесь определиться как между узлами “1” и “2”:
![]() В.
В.
Зная комплексные изображения тока в катушке индуктивности и напряжения на конденсаторе определим их мгновенные значения:
![]() А,
А,
![]() В.
В.
|
|
2) Цепь
в установившимся режиме после коммутации
|
|
Рис. 2.3.12.в |
 А,
А,
![]() В.
В.
Тогда мгновенные значения этих величин имеют вид:
![]() А;
А;
![]() В;
В;
![]() В.
В.
3) Расчет схемы в момент коммутации. Для
послекоммутационной схемы ( ключ К в
положении “2”) cоставляем
исходную систему из трех уравнений:
первое – по первому закону Кирхгофа
для узла “1”; второе – в соответствии
со вторым законом Кирхгофа для контура,
включающего источник ЭДС, катушку
индуктивности и конденсатор, третье –
по второму закону Кирхгофу для контура,
образованного из конденсатора и резистора![]()

где
![]()
Решим приведенную систему относительно
тока
![]() Для этого Из второго уравнения исходной
системы выразим напряжение
Для этого Из второго уравнения исходной
системы выразим напряжение![]() ,
а из третьего уравнения – ток
,
а из третьего уравнения – ток![]()
|
|
(2.3.25) |
|
|
(2.3.26) |
Подставим выражение (2.3.26) соотношение (2.3.25):

Выразим ток в конденсаторе через
полученное выше напряжение
![]()
![]()
Теперь подставим последние два тока в первое уравнение исходной системы:
![]()
После упрощений получаем следующее НДУ второго порядка:
![]()
Приравняв правую часть НДУ к нулю получаем ОДУ:
![]()
Отсюда составим характеристическое уравнение:
![]()
![]()
![]()
Определим его корни:
![]() с-1.
с-1.
Общее решение для тока в катушке индуктивности имеет вид:
![]()
Для упрощения объема вычислений будем
искать лишь свободную составляющую
тока –
![]() Решение для нее в случае двух комплексно
– сопряженных корней имеет вид:
Решение для нее в случае двух комплексно
– сопряженных корней имеет вид:
![]()
Для нахождения постоянных интегрирования
найдем производную по
![]() от последнего выражения:
от последнего выражения:
![]()
Составим систему из двух последних
уравнений, записанных при
![]()
|
|
(2.3.27) |
Найдем зависимые начальные условия –
![]() и
и![]() через независимые –
через независимые –![]() и
и![]() .
На основании законов коммутации имеем:
.
На основании законов коммутации имеем:
![]() А;
А;
![]() В.
В.
Тогда свободная составляющая тока в катушке индуктивности определиться как:
![]() А.
А.
Запишем уравнение (2.3.25)
при![]()
![]()
Отсюда определяем значение производной
от тока в индуктивности при
![]()
![]() В.
В.
Тогда
![]() В.
В.
Тогда система уравнений (2.3.27) предстанет в виде:

Выразив из первого уравнения данной
системы
![]() и подставив во второе, получаем:
и подставив во второе, получаем:
![]()
![]()
Следовательно, свободная составляющая тока в индуктивности
![]() А.
А.
Запишем решение для свободной составляющей напряжения на конденсаторе:
![]()
Для нахождения постоянных интегрирования
![]() и
и![]() найдем выражения для свободной
составляющей тока в конденсаторе
найдем выражения для свободной
составляющей тока в конденсаторе
![]()
и составим систему
из двух последних выражений, записанных
при
![]()
|
|
(2.3.28) |
Определим
![]() :
:
![]() В.
В.
Теперь определим![]() .
Для этого запишем первое уравнение
исходной системы уравнений при
.
Для этого запишем первое уравнение
исходной системы уравнений при![]()
![]()
Следовательно,
![]() А.
А.
где значение
![]() определяется подстановкой
определяется подстановкой![]() в уравнение (2.3.26):
в уравнение (2.3.26):
![]() А.
А.
Тогда
![]() А.
А.
Тогда система уравнений (2.3.28) принимает следующий вид:
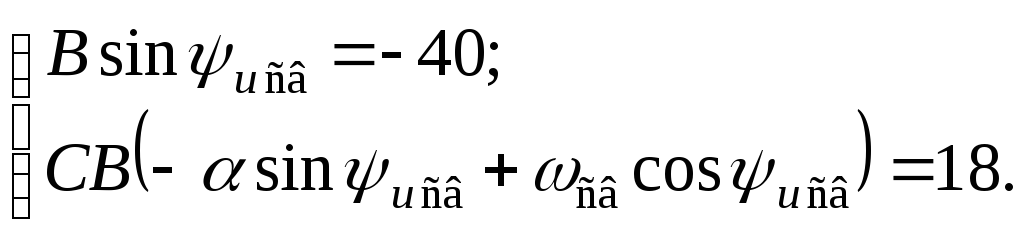
Совместное решение этой системы уравнений дает следующие результаты:
![]()
![]() В.
В.
Итак, свободное напряжение
![]() А.
А.
Окончательно запишем полные выражения для тока в катушке и напряжения на конденсаторе:
![]() А;
А;
![]() В.
В.
Задача 2.3.13Цепь, представленная на
рис. 2.3.13.а, питается от источника
синусоидальной ЭДС![]() В. Параметры цепи:
В. Параметры цепи:![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом,
Ом,![]() Гн,
Гн,![]() мкФ.
Определить ток в катушке индуктивности
мкФ.
Определить ток в катушке индуктивности![]() и напряжение на емкости
и напряжение на емкости![]() после замыкания ключа К.
после замыкания ключа К.
|
|
|
|
Рис. 2.3.13.а |
Рис. 2.3.13.б |
Решение
Составим план решения задачи:
1) Расчет цепи до коммутации;
2) Расчет цепи после коммутации;
3) Составление характеристического уравнения способом алгебраизации дифференциальных уравнений.
Общее решение для временных функций представим как:
![]()
![]()
Далее рассуждения будем вести относительно свободных составляющих токов и напряжений.
4) Определение независимых начальных условий, а также начальных значений для свободных составляющих;
5) Определение постоянных интегрирования;
6) Определение полных выражений для искомых функций путем суммирования принужденных и свободных составляющих токов и напряжений.
1) Расчет цепи до коммутации.
Определим реактивные сопротивления приемников:
![]() Ом.
Ом.
![]() Ом.
Ом.
Комплексное изображение источника ЭДС:
![]() В.
В.
Эквивалентное сопротивление цепи
![]()
![]() Ом.
Ом.
Находим комплекс тока во входной ветви
![]() А.
А.
Согласно методу “чужой” ветви определяем комплекс тока в первой ветви:

На основании закона Ома рассчитываем комплексное изображение напряжения на конденсаторе:
![]() В.
В.
Тогда его мгновенное значение определится как:
![]() В.
В.
2) Расчет принужденных составляющих.
|
|
|
|
Рис. 2.3.13.в |
Рис. 2.3.13.г |
Схема, соответствующая работе цепи после коммутации изображена на рис. 4.3.х.в. На рис. 2.3.13.г составлена схема для комплексных изображений токов. Для этой схемы введены следующие комплексные сопротивления приемников:
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом.
Ом.
Упростим данную схему путем преобразования
треугольника сопротивлений
![]()
![]() и
и![]() в звезду комплексных сопротивлений
в звезду комплексных сопротивлений![]()
![]() и
и![]()
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом.
Ом.
|
|
Тогда получаем упрощенную эквивалентную схему, представленную на рис. 2.3.13.д, для которой теперь можно легко определить искомые комплексы токов. Найдем эквивалентное комплексное сопротивление данной цепи:
По закону Ома определяем комплекс тока во |
|
Рис. 2.3.13.д |
входной ветви:
![]() А.
А.
Методом “чужой” ветви определяем ток
![]()
![]()
![]() А.
А.
По закону Ома находим напряжение на конденсаторе:
![]() В.
В.
По первому закону Кирхгофа для узла “1”
определяем ток
![]()
![]() А.
А.
Тока
![]() найдем через напряжение между узлами
“4” и “3”, определяемого с помощью
второго закона Кирхгофа применительно
для схемы, изображенной на рис. 2.3.13.д:
найдем через напряжение между узлами
“4” и “3”, определяемого с помощью
второго закона Кирхгофа применительно
для схемы, изображенной на рис. 2.3.13.д:
![]() В.
В.
Тогда для схемы, вычерченной на рис.
2.3.13.е, в соответствии с законом Ома легко
рассчитываем комплекс тока в катушке
индуктивности
![]()
![]() А.
А.
Найдем напряжение на индуктивном элементе:
![]() В.
В.
Теперь перейдем от комплексных изображений тока в катушке и конденсаторе. а также напряжения на конденсаторе, индуктивности к их мгновенным значениям:
![]() А;
А;
![]() А;
А;
![]() В;
В;
![]() В.
В.
3) Составление характеристического
уравнения
![]() Запишем исходную систему уравнений,
составленных на основании первого и
второго законов Кирхгофа для цепи,
приведенной на рис. 2.3.13.а (ключ К замкнут):
Запишем исходную систему уравнений,
составленных на основании первого и
второго законов Кирхгофа для цепи,
приведенной на рис. 2.3.13.а (ключ К замкнут):
|
|
(2.3.29) |
|
(2.3.30) | |
|
(2.3.31) | |
|
(2.3.32) | |
|
(2.3.33) | |
|
(2.3.34) |
Составим ОДУ относительно тока
![]() Из
уравнения (2.3.29) и (2.3.30) токи
Из
уравнения (2.3.29) и (2.3.30) токи
![]() ,
,
![]() подставим в выражение (2.3.31):
подставим в выражение (2.3.31):
|
|
(2.3.35) |
Выразив из уравнения (2.3.31) ток
![]() и
подставив его, а также ток
и
подставив его, а также ток
![]() в уравнение (2.3.33), получим:
в уравнение (2.3.33), получим:
|
|
(2.3.36) |
Подставим в выражение (2.3.34) токи
![]() и
и
![]() :
:
|
|
(2.3.37) |
Запишем уравнения (2.3.35), (2.3.36) и (2.3.37) относительно свободных составляющих и сделаем группировку слагаемых. В результате получим систему однородных дифференциальных уравнений:

Проведем так называемую алгебраизацию полученной системы уравнений (т.е. переход от дифференциальных уравнений к алгебраическим): для этого напряжение на конденсаторе представим как:
![]() ,
,
где
![]() – постоянная интегрирования.
– постоянная интегрирования.
Отметим, что при интегрировании отсутствует постоянная интегрирования, так как у свободных составляющих их по определению быть не может.
Аналогично напряжение на индуктивности представим как:
![]()
где
![]() – постоянная интегрирования.
– постоянная интегрирования.
В результате после группировки слагаемых получим систему алгебраических уравнений:
|
|
(2.3.38) |
Для того чтобы свободные токи системы
уравнений (2.3.38)
![]()
![]() были неравны нулю, необходимо, чтобы
определитель этой системы
были неравны нулю, необходимо, чтобы
определитель этой системы
![]() был равен нулю (так как определители
был равен нулю (так как определители
![]() ,
получаемые из алгебраических дополнений
главного определителя
,
получаемые из алгебраических дополнений
главного определителя
![]() равны нулю в силу равенства нулю всех
слагаемых в правой части системы
уравнений (2.3.36):
равны нулю в силу равенства нулю всех
слагаемых в правой части системы
уравнений (2.3.36):
![]() ):
):

откуда получаем характеристическое уравнение:
![]()
или
![]()
Корни этого уравнения
![]()
получаются комплексно – сопряженными, следовательно, переходный процесс имеет колебательный характер.
Запишем общее выражение для искомых временных функций:
![]()
![]()
4) Для расчета переходного процесса
предварительно рассчитаем зависимые
начальные условия – значения свободных
составляющих при
![]()
![]()
![]()
![]() и
и
![]()
Для этого составим исходную систему
из уравнений (2.3.29) – (2.3.34)
![]()
|
|
(2.3.39) |
Здесь
![]() и
и
![]() – независимые начальные условия,
определяемые на основании законов
коммутации:
– независимые начальные условия,
определяемые на основании законов
коммутации:
![]()
![]() В.
В.
Так как
![]() то из второго и третьего уравнений
системы (2.3.39) можно записать:
то из второго и третьего уравнений
системы (2.3.39) можно записать:
![]()
![]()
Подставим два последних соотношения в четвертое и пятое и шестое уравнения системы (2.3.39):
|
|
(2.3.40) |
Выразим ток
![]() из первого уравнения системы (2.3.39) и
подставим во второе и третье уравнение
системы уравнений (2.3.40) и сгруппируем
слагаемые. В итоге получаем:
из первого уравнения системы (2.3.39) и
подставим во второе и третье уравнение
системы уравнений (2.3.40) и сгруппируем
слагаемые. В итоге получаем:

Совместно решая приведенную систему
находим искомые токи
![]() и
и
![]()

![]() А;
А;

![]() А,
А,
где
![]() В.
В.
Из третьего уравнения системы уравнений (2.3.40) находим начальное значение напряжения на индуктивном элементе:
![]() В.
В.
Рассчитаем начальные значения свободных составляющих следующим образом:
![]() А;
А;
![]() А;
А;
![]() В;
В;
![]() В.
В.
4) Определение постоянных интегрирования.
Запишем общее решение ОДУ для тока
![]() в случае колебательного процесса:
в случае колебательного процесса:
![]()
Для нахождения постоянных интегрирования
![]() и
и
![]() определим выражение для свободой
составляющей напряжения на индуктивности:
определим выражение для свободой
составляющей напряжения на индуктивности:
![]() .
.
Теперь, используя два последних уравнения и начальные условия, составим систему уравнений:

Выразив из первого уравнения системы
 и
подставив во второе уравнение, получим:
и
подставив во второе уравнение, получим:
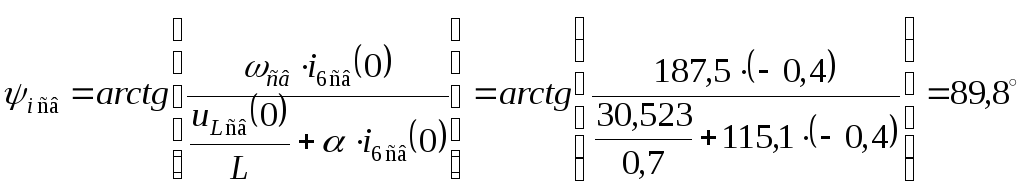 ;
;
 .
.
Итак, закон изменения тока в катушке
![]() А.
А.
Проверка:
![]()
6) Запишем выражение для напряжения
![]()
![]()
Для нахождения постоянных интегрирования
![]() и
и
![]() определим выражение для свободой
составляющей тока, протекающего через
конденсатор:
определим выражение для свободой
составляющей тока, протекающего через
конденсатор:
![]() .
.
Используя два последних уравнения и начальные условия, составим систему уравнений:
 .
.
Выразив из первого уравнения системы
 и
подставив во второе уравнение, получим:
и
подставив во второе уравнение, получим:
 ;
;

Итак, закон изменения напряжения
![]() В.
В.
Проверка:
![]() В.
В.
2.4 Примеры расчета переходных процессов в цепях со взаимоиндуктивностью
Задача 2.4.1Цепь, изображенная на
рис. 2.4.4.а, подключена к источнику
постоянного тока
![]() А. Параметры цепи:
А. Параметры цепи:
![]() Ом;
Ом;
![]() мГн;
мГн;
![]() мГн. Найти токи
мГн. Найти токи
![]() и
и
![]()
|
|
|
|
Рис. 2.4.1.а |
Рис. 2.4.1.б |
Решение
1) Цепь до коммутации
![]() представлена на рис. 2.4.1.б. Ток
представлена на рис. 2.4.1.б. Ток
![]() равен току источника
равен току источника
![]()
![]() А,
А,
тогда
![]()
2) Цепь после коммутации
![]() вычерчена на рис. 2.4.1.б. Падения напряжения
на индуктивных элементах на постоянном
токе равны нулю. Определим ток
вычерчена на рис. 2.4.1.б. Падения напряжения
на индуктивных элементах на постоянном
токе равны нулю. Определим ток
![]() методом “чужой ветви”:
методом “чужой ветви”:
![]() А.
А.
По первому закону Кирхгофа для узла “1”
найдем ток
![]()
![]() А.
А.
3) Для цепи, изображенной на рис. 2.4.1.а, в
момент замыкания ключа К составим
систему из двух уравнений: первое – на
основании первого закона Кирхгофа для
узла “1” и второе – по второму закону
Кирхгофа для контура
![]()

Из первого уравнения системы выразим
ток
![]()
|
|
(2.4.1) |
Подставим (2.4.1) во второе уравнение исходной системы:
![]()
После упрощений окончательно получаем НДУ первого порядка:
|
|
(2.4.2) |
Приравняв слагаемое
![]() к нулю получаем ОДУ первого порядка:
к нулю получаем ОДУ первого порядка:
![]()
Отсюда составим характеристическое уравнение:
![]()
Определим его корень:
![]() с-1.
с-1.
Общее решение НДУ (4.4.2) в случае единственного отрицательного и действительного корня имеет вид:
![]()
Постоянную интегрирования
![]() найдем из последнего уравнения,
записанного при
найдем из последнего уравнения,
записанного при
![]()
![]()
где
![]() ток в катушке момент коммутации,
ток в катушке момент коммутации,
![]() А – по первому закону коммутации.
А – по первому закону коммутации.
Тогда имеем:
![]()
откуда
![]()
Окончательно получим:
![]() А.
А.
Определим ток
![]() по соотношению (2.4.1):
по соотношению (2.4.1):
![]() А.
А.
Задача 2.4.2Цепь, изображенная на
рис. 2.2.2.а, питается от источника постоянной
ЭДС
![]() В. В момент
В. В момент
![]() происходит срабатывание ключа К. в
результате чего в цепи начинается
переходной процесс. Найти закон изменения
во времени токов
происходит срабатывание ключа К. в
результате чего в цепи начинается
переходной процесс. Найти закон изменения
во времени токов
![]() и
и
![]() Известны параметры цепи:
Известны параметры цепи:
![]() Ом,
Ом,
![]() мГн,
мГн,
![]() мГн.
мГн.
Решение
1) Цепь до коммутации изображена на рис. 2.4.2.б, в которой ток определяется в соответствии с законом Ома:
![]() А.
А.
Так как ветвь с другой катушкой отключена, следовательно
![]()
|
|
|
|
Рис. 2.4.2.а |
Рис. 2.4.2.б |
|
|
2) Цепь
после коммутации представлена на рис.
2.4.2.в. На постоянном токе падение
напряжения от магнитной связи катушек
и их собственной индуктивности нет (
По закону Ома определяем ток источника ЭДС: |
|
Рис. 2.4.2.в |
![]() А.
А.
Согласно методу “чужой” ветви с учетом равенства сопротивлений резисторов получаем:
![]() А.
А.
3) Для схемы, изображенной на рис. 2.4.2.а в момент коммутации (К замкнут) для расчета переходного процесса составляем исходную систему из трех уравнений с учетом встречного включения катушек индуктивности:

Решим эту систему относительно тока
![]()
Подставим первое уравнение системы во второе:
![]()
или
|
|
(2.4.3) |
Сложим почленно выражение (2.4.3) с третьим уравнением исходной системы уравнений:
![]()
Сгруппировав слагаемые, получаем уравнение
![]()
из которого выражаем производную от
тока
![]() по
по
![]()
|
|
(2.4.4) |
Подставим (2.4.4) в уравнение (2.4.3):
![]()
Раскрыв скобки, избавившись от выражения
![]() в знаменателе и сгруппировав слагаемые,
получим следующее соотношение:
в знаменателе и сгруппировав слагаемые,
получим следующее соотношение:
|
|
(2.4.5) |
Продифференцируем (2.4.5) по
![]()
![]()
Исключим из последнего уравнения
слагаемое
![]() .
Для этого введем сюда подстановку
.
Для этого введем сюда подстановку
![]() из (2.4.4):
из (2.4.4):
![]()
Сделав ряд преобразований в последнем
выражении, окончательно получаем НДУ
второго порядка, записанного для тока
![]()
![]()
Приравняв правую часть к нулю, получаем ОДУ второго порядка:
![]()
Отсюда составляем характеристическое уравнение:
![]()
![]()
![]()
Определяем корни характеристического уравнения:
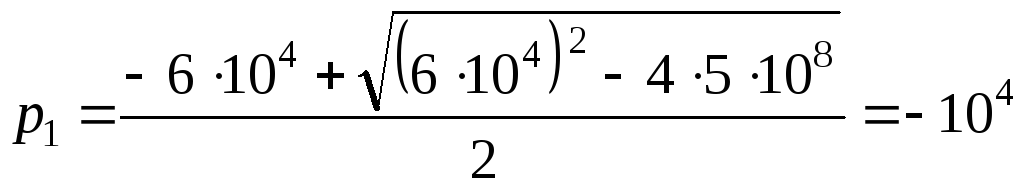 с-1;
с-1;
 с-1.
с-1.
Запишем общее решение НДУ для тока
![]() с учетом двух отрицательных и действительных
корнях характеристического уравнения:
с учетом двух отрицательных и действительных
корнях характеристического уравнения:
|
|
(2.4.6) |
Для нахождения постоянных интегрирования
![]() и
и
![]() составим дополнительное уравнение,
путем дифференцирования выражения
(2.4.6):
составим дополнительное уравнение,
путем дифференцирования выражения
(2.4.6):
![]()
Теперь составим систему последнего
уравнения и выражения (4.4.5), подставив
туда время
![]()
|
|
(2.4.7) |
где
![]() – начальное значение тока
– начальное значение тока
![]() определяемое по первому закону коммутации:
определяемое по первому закону коммутации:
![]() А;
А;
![]() – начальное значение первой производной
от тока
– начальное значение первой производной
от тока
![]() Для его определения запишем уравнение
(2.4.5) при
Для его определения запишем уравнение
(2.4.5) при
![]()
![]()
где
![]() – начальное значение тока
– начальное значение тока
![]() определяемое по первому закону коммутации:
определяемое по первому закону коммутации:
![]() А.
А.
Тогда
![]()
Откуда получаем:
![]() А/с.
А/с.
Таким образом, подставляя найденные
начальные значения
![]() и
и
![]() в систему уравнений (2.4.7), имеем:
в систему уравнений (2.4.7), имеем:

Совместное решение последней системы уравнений дает результаты:
![]()
![]()
Подставляя все известные величины в
(2.4.6), окончательно получаем выражение
для переходного тока
![]()
![]() А.
А.
Запишем общее выражение для тока
![]() с учетом полученных корней характеристического
уравнения:
с учетом полученных корней характеристического
уравнения:
|
|
(2.4.8) |
Запишем производную от этого тока путем дифференцирования (4.4.8):
![]()
Составим систему из двух последних
выражений, записанных при
![]()
|
|
(2.4.9) |
![]() – начальное значение первой производной
от тока
– начальное значение первой производной
от тока
![]() определяемое из соотношения запишем
уравнение (2.4.4) при
определяемое из соотношения запишем
уравнение (2.4.4) при
![]()
![]() А/с.
А/с.
Тогда система уравнений (2.4.9) предстанет в виде:

Совместное ее решение дает следующие результаты:
![]()
![]()
Тогда окончательно получаем следующий ток:
![]() А.
А.
Задача 2.4.3В электрической цепи,
представленной на рис. 2.4.3.а, определить
токи после замыкания ключа К, если
![]() В,
В,
![]()
![]()
|
|
Решение 1) В цепи до коммутации отсутствует источник ЭДС, поэтому в соответствии с первым законом коммутации имеем следующие независимые начальные условия:
2) Определи принужденные составляющие токов. На постоянном токе падение напряжения от магнитной связи катушек и их собственной индуктивности нет, |
|
Рис. 2.4.3.а |
в данной цепи имеются только резисторы. Эквивалентное сопротивление цепи:
![]() Ом.
Ом.
По закону Ома определяем ток источника
ЭДС:
![]()
Согласно методу “чужой” ветви с учетом равенства сопротивлений резисторов получаем:

3) С учетом независимых начальных условий, определим зависимые начальные условия:
![]()
Найдем начальные значения производных
от токов:
![]() и
и
![]() ,
для этого составим систему уравнений
по законам Кирхгофа для момента времени
,
для этого составим систему уравнений
по законам Кирхгофа для момента времени
![]()

Так как
![]() получим:
получим:

Из второго уравнения последней системы
уравнений выразим производную
![]() и подставим в первое уравнение этой же
системы:
и подставим в первое уравнение этой же
системы:
![]()
![]()
Отсюда следует, что

4) Корни характеристического уравнения
можно найти аналогично задаче 2.4.2, или
более просто из операторного сопротивления
![]() ,
осуществив развязку магнитосвязанных
контуров. Послекоммутационная схема с
развязкой катушек показана на рис.
2.4.3.б.
,
осуществив развязку магнитосвязанных
контуров. Послекоммутационная схема с
развязкой катушек показана на рис.
2.4.3.б.
|
|
|
|
Рис. 2.4.3.б |
Характеристическое уравнение:
![]() откуда
откуда

Запишем общее решение НДУ для тока
![]() с учетом двух отрицательных и действительных
корнях характеристического уравнения:
с учетом двух отрицательных и действительных
корнях характеристического уравнения:
|
|
(2.4.10) |
Для нахождения постоянных интегрирования
![]() и
и
![]() составим дополнительное уравнение,
путем дифференцирования выражения
(2.4.10) для тока
составим дополнительное уравнение,
путем дифференцирования выражения
(2.4.10) для тока
![]() :
:
![]()
Определим постоянные интегрирования из начальных условий:

Совместное решение последней системы уравнений дает результаты:
![]()
Окончательно получаем выражение для
переходного тока
![]()
![]() А.
А.
Запишем общее выражение для тока
![]() :
:
![]()
Запишем производную от этого тока:
![]()
Составим систему из двух последних
выражений, записанных при
![]()

Совместное ее решение дает следующие результаты:
![]()
Тогда окончательно получим:
![]()
Ток во второй ветви получим на основании первого закона Кирхгофа:
![]()
Задача 2.4.4Воздушный трансформатор,
изображенный на рис. 2.4.4.а, с нагрузкой
![]() Ом в момент времени
Ом в момент времени
![]() подключается к источнику синусоидальной
ЭДС
подключается к источнику синусоидальной
ЭДС
![]() В. Параметры трансформатора:
В. Параметры трансформатора:
![]() Ом,
Ом,
![]() Гн,
Гн,
![]() Гн,
Гн,
![]() Гн. Определить ток в нагрузке
Гн. Определить ток в нагрузке
![]()
|
|
|
|
Рис. 2.4.4.а |
Рис. 2.4.4.б |
1) В цепи начальные условия, т.е.
![]()
![]()
2) Определим принужденную составляющую
тока в нагрузке
![]() для чего вычертим на рис. 2.4.4.б схему,
соответствующую установившемуся режиму
работы цепи после коммутации
для чего вычертим на рис. 2.4.4.б схему,
соответствующую установившемуся режиму
работы цепи после коммутации
![]() Для этого запишем уравнения по законам
Кирхгофа в комплексной форме:
Для этого запишем уравнения по законам
Кирхгофа в комплексной форме:

Здесь
![]() и
и
![]() и
и
![]() – комплексные сопротивления,
– комплексные сопротивления,
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() – амплитуда комплексного изображения
ЭДС,
– амплитуда комплексного изображения
ЭДС,
![]() В.
В.
Из совместного решения приведенной выше системы уравнений получаем:
![]() А.
А.
Тогда мгновенное значения тока в нагрузке
![]() А.
А.
3) Для цепи, изображенной на рис. 2.4.4.б, в
момент
![]() когда ключ К замкнут, составляем исходную
систему из двух уравнений: первое – по
второму закону Кирхгофа для контура с
источником ЭДС и катушкой с индуктивностью
когда ключ К замкнут, составляем исходную
систему из двух уравнений: первое – по
второму закону Кирхгофа для контура с
источником ЭДС и катушкой с индуктивностью
![]() второе – по второму закону Кирхгофа
для контура с нагрузкой катушкой с
индуктивностью
второе – по второму закону Кирхгофа
для контура с нагрузкой катушкой с
индуктивностью
![]() с учетом согласного включения катушек:
с учетом согласного включения катушек:
|
|
(2.4.11) |
Из второго уравнения системы (2.4.11) имеем:
|
|
(2.4.12) |
Подставим (2.4.12) в первое уравнение исходной системы (2.4.11):
![]()
Продифференцируем полученное выражение:
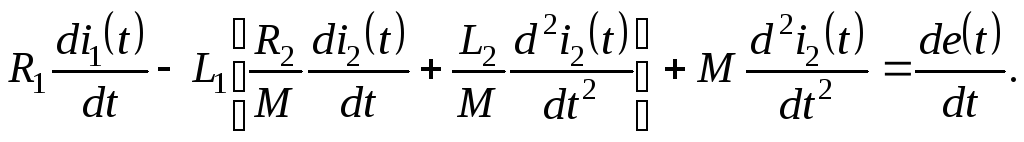
Снова сделаем подстановку (2.4.12) в последнее выражение:

После несложных преобразований получаем НДУ второго порядка:
![]()
Приравняв правую часть данного НДУ к нулю получим ОДУ второго порядка:
![]()
Отсюда получаем следующее характеристическое уравнение:
![]()
![]()
![]()
Определим корни этого уравнения: