- •Министерство образования и науки Российской Федерации
- •Введение
- •Перечень условных обозначений
- •1 Основные теоретические положения
- •1.1. Физические основы переходных процессов
- •1.2 Математический аппарат и алгоритмы расчетов
- •1.2.1 Классический метод анализа переходного процесса
- •1.2.2 Операторный метод расчета (метод преобразования Лапласа)
- •1.2.3 Расчет методом интеграла Дюамеля
- •1.2.4 Метод переменных состояния переходных процессов
- •2 Классический метод расчета переходных процессов в линейных электрических цепях
- •2.1 Примеры расчета переходных процессов в цепях с индуктивностью
- •Имеет один отрицательный и действительный корень
- •Решение
- •И подставим его в первое уравнение системы:
- •Источника напряжения
- •Получим характеристическое уравнение
- •Решение
- •Первый способ
- •Решение
- •Ом; Ом.
- •Решение
- •Решение
- •И падение напряжение на индуктивности
- •Решение
- •Поэтому в соответствии с первым законом Кирхгофа для узла “1” ток в индуктивности, питаемый источником тока равен току в ветви с резистором: а.
- •Откуда составляем характеристическое уравнение:
- •Где ток в конденсаторе.
- •Отсюда находим характеристическое уравнение:
- •С-1; с-1.
- •С-1; с-1.
- •Решение
- •Напряжение между узлами 1 и 2 определяется как:
- •И подставим туда ток конденсатора (2.6.6):
- •Откуда характеристическое уравнение оду будет иметь вид:
- •2.8 Задачи для самостоятельного решения
- •3 Операторный метод расчета переходных процессов в линейных электрических цепях
- •3.1 Примеры расчета переходных процессов в цепях постоянного тока
- •Решение
- •Решение
- •3.2 Примеры расчета переходных процессов в цепях переменного тока
- •С-1; с-1;
- •По закону Ома для участка цепи определяем искомый операторный ток:
- •С-1; с-1;
- •4 Расчет переходных процессов с помощью интеграла дюамеля
- •4.1 Примеры расчета переходных и импульсных характеристик
- •Тогда по закону Ома в операторной форме определяем ток
- •Решение
- •С-1; с-1;
- •4.2 Примеры расчета переходных процессов с помощью интеграла Дюамеля
- •Решение
- •4.3 Задачи для самостоятельного решения
- •5 Расчет переходных процессов методом переменных состояния
- •5.1 Примеры расчета
- •Определим собственные значения матрицы a, т.Е. Корни уравнения
- •. Определим собственные значения матрицы a, т.Е. Корни уравнения
- •5.2 Задачи для самостоятельного решения
- •Список литературы
- •Содержание
- •Часть II
- •190008, Г.С.-Петербург, ул. Лоцманская, 3.
1.2.4 Метод переменных состояния переходных процессов
Для линейной цепи ток каждой ветви и напряжение можно найти как решение составленного для этой ветви дифференциального уравнения, полученного из системы уравнений по законам Кирхгофа:
|
|
(1.2.1) |
Заменим неизвестную величину
![]() и ее производные переменными:
и ее производные переменными:
![]()
![]()
![]()
![]()
При такой замене уравнение (1.2.1) будет сводиться к системе дифференциальных уравнений первого порядка:
|
|
(1.2.2) |
|
|
Переменными состояния являются переменная
![]() и ее производные.
и ее производные.
На переходной процесс в любой электрической
цепи влияют параметры цепи, параметры
источников энергии и независимые
начальные условия (токи в индуктивных
элементах и напряжения на емкостных
элементах коммутации). Поэтому в качестве
переменных состояния целесообразно
здесь выбирать токи в катушках и
напряжения на конденсаторах. За входные
величины примем источники электрической
энергии![]() за выходные – искомые величины
за выходные – искомые величины![]() .
.
Запишем дифференциальное уравнение состояния в матричной форме:
|
|
(1.2.3) |
или
|
|
(1.2.4) |
где
![]() – матрица – столбец переменных состояния
размером
– матрица – столбец переменных состояния
размером![]()
![]() – матрица – столбец электродвижущих
сил и токов источников размером
– матрица – столбец электродвижущих
сил и токов источников размером![]()
![]() – основная квадратная матрица порядка
– основная квадратная матрица порядка![]()
![]() – матрица связи размера
– матрица связи размера![]() Элементы указанных матриц определяются
структурой и параметрами цепи.
Элементы указанных матриц определяются
структурой и параметрами цепи.
Уравнения (1.2.3) и (1.2.4) в матричной форме
можно составить с применением метода
наложения по законам Кирхгофа и других
методов. Для получения зависимостей
между производными переменных состояния,
т.е.
![]()
![]() и переменными состояния
и переменными состояния![]() и
и![]() а также ЭДС и токами источников, будем
полагать, что переменные состояния
заданы.
а также ЭДС и токами источников, будем
полагать, что переменные состояния
заданы.
2 Классический метод расчета переходных процессов в линейных электрических цепях
2.1 Примеры расчета переходных процессов в цепях с индуктивностью
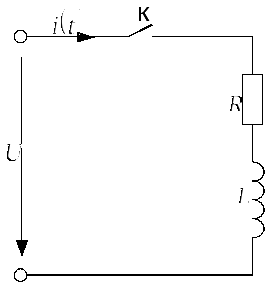
Задача 2.1.1Цепь, представленная на
рис. 2.1.1.а, содержит последовательно
соединенные резистор с сопротивлением![]() Ом и катушку с индуктивностью
Ом и катушку с индуктивностью![]() Гн,
при замыкании ключа К в момент
Гн,
при замыкании ключа К в момент![]() включается на постоянное напряжение
включается на постоянное напряжение![]() В. С какой скоростью нарастает ток в
начальный момент времени? Определить
через какой промежуток времени ток
станет равным 99% тока установившегося
режима. Найти закон изменения ЭДС
самоиндукции, наводимой при включении,
и вычислить, через какой промежуток
времени после включения скорость
нарастания энергии в магнитном поле
В. С какой скоростью нарастает ток в
начальный момент времени? Определить
через какой промежуток времени ток
станет равным 99% тока установившегося
режима. Найти закон изменения ЭДС
самоиндукции, наводимой при включении,
и вычислить, через какой промежуток
времени после включения скорость
нарастания энергии в магнитном поле![]() будет максимальна.
будет максимальна.
|
|
Решение 1) До
коммутации
2)
Рассчитаем ток в катушке после
коммутации
3) Для
расчета переходного процесса в схеме,
представленной на рис. 2.1.1.а, в момент
коммутации
которое является НДУ первого порядка. Из последнего уравнения определим ОДУ:
и характеристическое уравнение
|
|
Рис. 2.1.1.а | |
|
| |
|
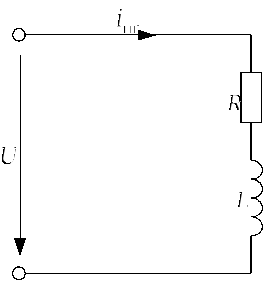
Рис. 2.1.1.б |
Корень последнего уравнения
![]() с-1
с-1
единственный, отрицательный и действительный.
Общее решение составленного НДУ при одном отрицательном корне имеет вид:
![]()
Постоянную интегрирования
![]() определим из начальных условий: для
этого запишем последнее уравнение при
определим из начальных условий: для
этого запишем последнее уравнение при![]()
![]()
Так как в соответствии с первым законом
коммутации ток в катушке индуктивности
![]() не может изменяться скачком и должен
быть равен току при
не может изменяться скачком и должен
быть равен току при![]() т.е.
т.е.
![]()
Тогда
![]()
Окончательное решение для тока в катушке
![]() А.
А.
4) Производная тока в катушке
![]()
Скорость нарастания тока в катушке в начальный момент времени
![]() А/с.
А/с.
5) Промежуток времени, через который ток станет равным 99% тока установившегося режима определим следующим образом:
![]()
или
![]()
![]()
![]() мс.
мс.
6) Определим закон изменения ЭДС самоиндукции, наводимой в катушке индуктиности при замыкании ключа К:
![]() В.
В.
7) Найдем промежуток времени после
включения
![]() ,
через которой скорость нарастания
энергии в магнитном поле
,
через которой скорость нарастания
энергии в магнитном поле![]() будет максимальна. Для этого сначала
вычислим выражение для энергии в
магнитном поле катушки индуктивности:
будет максимальна. Для этого сначала
вычислим выражение для энергии в
магнитном поле катушки индуктивности:
![]()
![]() Дж.
Дж.
Скорость нарастания энергии

Найдем максимум последней функции:
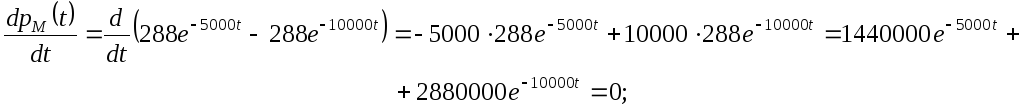
![]()
![]()
откуда
![]() мс.
мс.
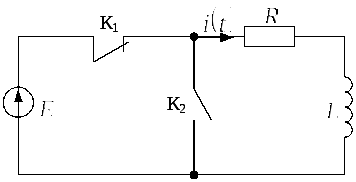
Задача 2.1.2 На рис. 2.1.2.а изображена
простейшая![]() цепь. Сопротивление катушки
цепь. Сопротивление катушки![]() Ом, ее индуктивность
Ом, ее индуктивность![]() Гн. До коммутации в цепи был установившейся
режим и через катушку проходил ток 20 А.
В момент
Гн. До коммутации в цепи был установившейся
режим и через катушку проходил ток 20 А.
В момент![]() она замыкается накоротко путем отключения
ключа К1и включения ключа К2.
Определить скорость убывания тока в
катушке в начальный момент времени и в
момент, когда ток равен 10 А.
она замыкается накоротко путем отключения
ключа К1и включения ключа К2.
Определить скорость убывания тока в
катушке в начальный момент времени и в
момент, когда ток равен 10 А.
|
|
|
|
Рис. 2.1.2.а |
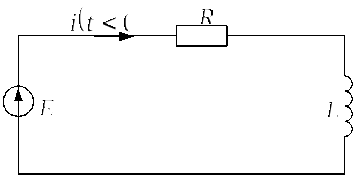
Рис. 2.1.2.б |
Решение
1) Схема до коммутации
![]() приведена на рис. 2.1.2.б. Согласно условию
задачи ток в катушке до коммутации
приведена на рис. 2.1.2.б. Согласно условию
задачи ток в катушке до коммутации
![]() А.
А.
|
|
2)
Вычерчиваем цепь для установившегося
режима. Схема для
3) Для расчета переходного процесса в
момент коммутации
|
|
Рис. 2.1.2.в |
Данное уравнение является НДУ первого порядка, которое в силу равенства нулю правой части совпадает с ОДУ
![]()
Характеристическое уравнение
![]()