Определим собственные значения матрицы a, т.Е. Корни уравнения

откуда получаем:

Матричная экспонента в системе второго порядка имеет вид:

либо в обычной системой алгебраических уравнений:

Тогда отсюда определяем коэффициенты и

Далее по выражению определяем матричную экспоненту

Затем определяем матрицу-столбец начальных значений переменных состояния:

где i_L(0) иu_C(0) – независимые начальные условия, определяемые до режима коммутации. Найденные величины подставляем в уравнениеи получаем:

Из приведенного выражения определяем ток в катушке и напряжение на конденсаторе

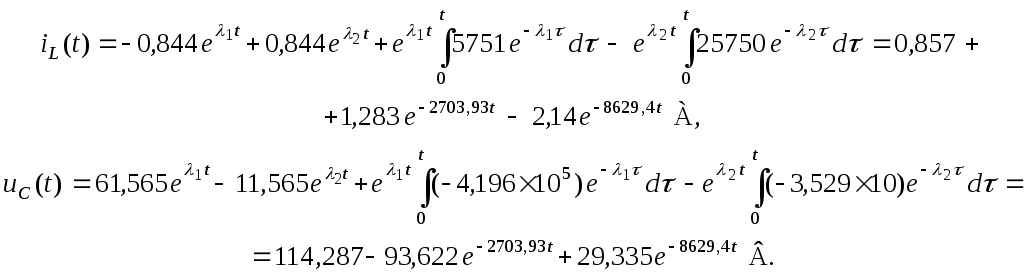
Задача 5.1.3В электрической цепи, представленной на рис. 5.1.3.a, в моментпроисходит замыкание ключа К. Определить ток в катушкеи напряжение на конденсатореметодом переменных состояния, если: В,Ом,Ом,Ом, мкФ, Гн.

	Решение Проведем расчет схемы до коммутации : Тогда запишем независимые начальные условия для данной цепи:
Рис. 5.1.3.а

В качестве переменных состояния выберем вектор .

Для схемы после коммутации покажем направленный топологический граф (рис. 5.1.3.б) и запишем для него уравнения по законам Кирхгофа:

	Выражая все токи и напряжения через ток катушки и напряжение на конденсаторе, получим систему уравнений, записанную относительно переменных состояния:
Рис. 5.1.3.б

Для упрощения, перепишем данную систему уравнений, заменив громоздкие выражения числовыми значениями:

или в матричной форме: ,

где

. Определим собственные значения матрицы a, т.Е. Корни уравнения

откуда получаем:

Полученные значения совпали с корнями характеристического уравнения задачи 2.3.13.

Как и в предыдущих задачах определяем коэффициенты из уравнений:

откуда

Далее по выражению определяем матричную экспоненту:

Запишем матрицу-столбец начальных значений переменных состояния:

где i_L(0) иu_C(0) – независимые начальные условия, которые были определены в начале решения задачи. Найденные величины подставляем в уравнениеи получаем:

Из приведенного выражения определяем ток в катушкеи напряжение на конденсаторе

5.2 Задачи для самостоятельного решения

	Задача 5.2.1На рис. 5.2.1 изображена цепь постоянного тока, запитанная источником токаА. В начальный момент времени замыкается ключ К. Найти ток в катушке индуктивностии напряжение на конденсаторе, при следующих параметрах цепи:Ом,Ом,Гн,мкФ.
Рис. 5.2.1
	Задача 5.2.2 В цепи, представленной на рис. 5.2.2 в момент временипроисходит коммутация – размыкание ключа К. Найти токеслиВ,Ом,Ом,Ом,мГн,мкФ.
Рис. 5.2.2
	Задача 5.2.3На рис. 5.2.3 изображена электрическая цепь с двумя источниками ЭДСВ иВ. В начальный момент времениключ К включает в цепь резисторНайти токи напряжение, при следующих параметрах цепи:Ом,Ом,мГн,мкФ.
Рис. 5.2.3

Задача 5.2.4Решить задачу 2.6.2 методом переменных состояния.

Задача 5.2.5 Решить задачу 3.3.3 методом переменных состояния.

Список литературы

1. Основы теории цепей: Учебник для вузов Зевеке Г.В., Ионкин П.А., Нетушин А.В., С.В.Страхов.- 5-е изд., перераб.- М.: Энергоатомиздат, 1989. – 528 с.: ил.

2. Шебес М.Р.Каблукова М.В. Задачник по теории линейных электрических цепей : Учеб. Пособ. Для электротехнич., радиотехничю спец. вузов. – 4-е изд.. перераб. и доп. – М.: Высш. шк., 1990. – 544 с.: ил.

3. Черевко А.И. Линейные электрические цепи. Л.: ЛКИ, 1989, ч.1, 53 с.

4.Теоретические основы электротехники: В 3-х т. Учебник для вузов. Том 1. – 4-е изд. /С.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. - СПб.:Питер, 2004. – 463 с.: ил.

5. Коровкин Н.В., Селина Е.Е., Чечурин В.Л. Теоретические основы электротехники: Сборник Задач. - СПб.:Питер, 2004. – 512 с.: ил. – (Серия «Учебное пособие»).

6. Беневоленский С.Б., Марченко А.Л. Основы электроники. Учебное пособие для втузов . – М.: Издательство Физико-математической литературы, 2007. – 568 с.: ил.

7. Сборник задач по теоретическим основам электротехники: Теоретические основы электротехники: Учебное пособие для энерг. И приборостр. Спец. Вузов. – 4-е изд., перераб. и испр. / Л.А. Бессонов, И.Г. Демидова, М.Е. Заруди и др.; Под ред. Л.А. Бессонова. – М.: Высш. шк., 2003. – 528 с.: ил.