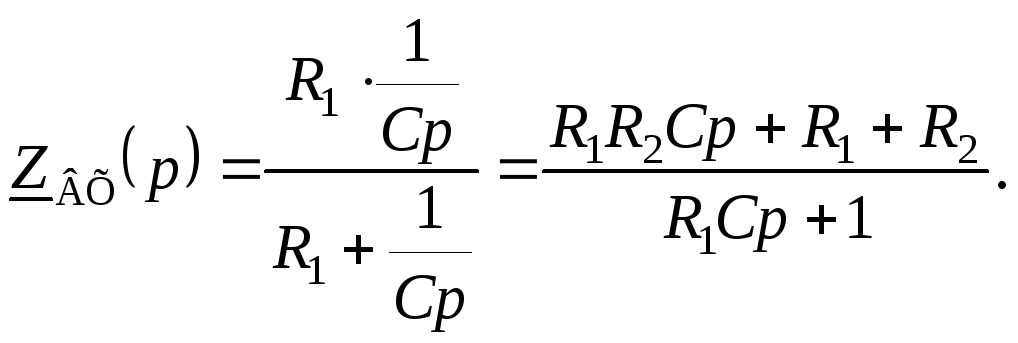- •Министерство образования и науки Российской Федерации
- •Введение
- •Перечень условных обозначений
- •1 Основные теоретические положения
- •1.1. Физические основы переходных процессов
- •1.2 Математический аппарат и алгоритмы расчетов
- •1.2.1 Классический метод анализа переходного процесса
- •1.2.2 Операторный метод расчета (метод преобразования Лапласа)
- •1.2.3 Расчет методом интеграла Дюамеля
- •1.2.4 Метод переменных состояния переходных процессов
- •2 Классический метод расчета переходных процессов в линейных электрических цепях
- •2.1 Примеры расчета переходных процессов в цепях с индуктивностью
- •Имеет один отрицательный и действительный корень
- •Решение
- •И подставим его в первое уравнение системы:
- •Источника напряжения
- •Получим характеристическое уравнение
- •Решение
- •Первый способ
- •Решение
- •Ом; Ом.
- •Решение
- •Решение
- •И падение напряжение на индуктивности
- •Решение
- •Поэтому в соответствии с первым законом Кирхгофа для узла “1” ток в индуктивности, питаемый источником тока равен току в ветви с резистором: а.
- •Откуда составляем характеристическое уравнение:
- •Где ток в конденсаторе.
- •Отсюда находим характеристическое уравнение:
- •С-1; с-1.
- •С-1; с-1.
- •Решение
- •Напряжение между узлами 1 и 2 определяется как:
- •И подставим туда ток конденсатора (2.6.6):
- •Откуда характеристическое уравнение оду будет иметь вид:
- •2.8 Задачи для самостоятельного решения
- •3 Операторный метод расчета переходных процессов в линейных электрических цепях
- •3.1 Примеры расчета переходных процессов в цепях постоянного тока
- •Решение
- •Решение
- •3.2 Примеры расчета переходных процессов в цепях переменного тока
- •С-1; с-1;
- •По закону Ома для участка цепи определяем искомый операторный ток:
- •С-1; с-1;
- •4 Расчет переходных процессов с помощью интеграла дюамеля
- •4.1 Примеры расчета переходных и импульсных характеристик
- •Тогда по закону Ома в операторной форме определяем ток
- •Решение
- •С-1; с-1;
- •4.2 Примеры расчета переходных процессов с помощью интеграла Дюамеля
- •Решение
- •4.3 Задачи для самостоятельного решения
- •5 Расчет переходных процессов методом переменных состояния
- •5.1 Примеры расчета
- •Определим собственные значения матрицы a, т.Е. Корни уравнения
- •. Определим собственные значения матрицы a, т.Е. Корни уравнения
- •5.2 Задачи для самостоятельного решения
- •Список литературы
- •Содержание
- •Часть II
- •190008, Г.С.-Петербург, ул. Лоцманская, 3.
4 Расчет переходных процессов с помощью интеграла дюамеля
4.1 Примеры расчета переходных и импульсных характеристик
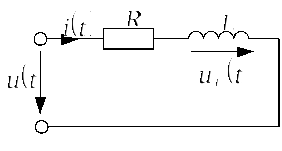
Задача 4.1.1 Определить переходную и
импульсную характеристики простейшей
последовательной![]() цепи, схема которой представлена на
рис. 4.1.1.а, с параметрами
цепи, схема которой представлена на
рис. 4.1.1.а, с параметрами![]() Ом и
Ом и![]() мГн. В качестве выходного напряжения
рассмотреть напряжение на индуктивности
мГн. В качестве выходного напряжения
рассмотреть напряжение на индуктивности![]()
|
|
Решение 1)
Определение переходных характеристик.
Найдем переходную проводимость
|
|
Рис. 4.1.1.а |
ток в цепи при подаче на вход схемы
единичной функции
![]() ).
).
Как известно из второй главы данного
пособия, ток при подключении
![]() цепи к источнику постоянного напряжения
цепи к источнику постоянного напряжения![]() определяется следующим выражением:
определяется следующим выражением:
![]()
Положив в этом уравнении
![]() получаем переходную проводимость цепи
получаем переходную проводимость цепи![]()
![]() См.
См.
По определению переходная функция –
это напряжение между какими – либо
двумя точками цепи при воздействии на
схему напряжения с амплитудой в 1 В. Т.е.
в нашем случае – это напряжение на
индуктивном элементе
![]() при воздействии на схему входного
напряжения
при воздействии на схему входного
напряжения![]() В. Найдем напряжение на индуктивности:
В. Найдем напряжение на индуктивности:
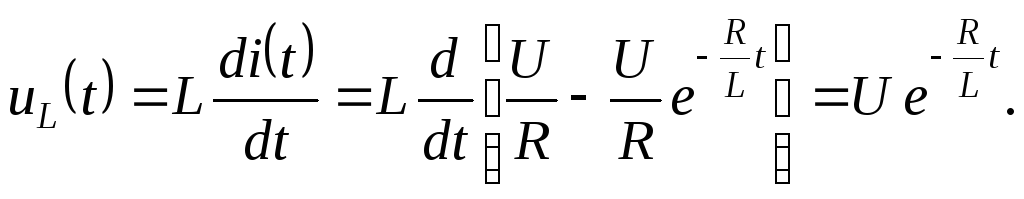
Тогда приняв здесь напряжение
![]() В, получим переходную функцию
В, получим переходную функцию![]()
![]()
2) Определение импульсных функций
(импульсной проводимости и импульсной
функции). Импульсные характеристики
определяют реакцию цепи на дельта –
функцию
![]() (функцию Дирака или единичную импульсную
функцию), поданную на вход схемы. Тогда
(функцию Дирака или единичную импульсную
функцию), поданную на вход схемы. Тогда![]() В данном случае реакцией цепи является
ток в катушке индуктивности (характеризуется
импульсной проводимостью) и напряжение
на индуктивности (характеризуется
импульсной функцией). Импульсную
проводимость
В данном случае реакцией цепи является
ток в катушке индуктивности (характеризуется
импульсной проводимостью) и напряжение
на индуктивности (характеризуется
импульсной функцией). Импульсную
проводимость![]() найдем через переходную проводимость
следующим соотношением:
найдем через переходную проводимость
следующим соотношением:
![]()
Здесь
![]() – значение найденной выше переходной
проводимости при
– значение найденной выше переходной
проводимости при![]()
![]()
Тогда получаем:
![]()
![]()
Импульсную функцию
![]() рассчитаем с помощью известной
зависимости:
рассчитаем с помощью известной
зависимости:
![]() с-1,
с-1,
где
![]() – значение найденной выше переходной
функции при
– значение найденной выше переходной
функции при![]()
![]()
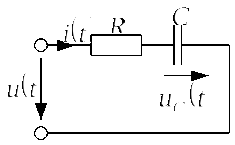
Задача 4.1.2 Определить переходные и
импульсные характеристики простейшей![]() цепи, изобиженной на рис. 4.1.2.а. Переходные
и импульсные функции рассчитать для
напряжения между обкладками конденсатора
цепи, изобиженной на рис. 4.1.2.а. Переходные
и импульсные функции рассчитать для
напряжения между обкладками конденсатора![]() Данные взять из задачи 2.2.2
Данные взять из задачи 2.2.2
|
|
Решение 1) Определение переходных характеристик. Выражение для переходного напряжения на конденсаторе имеет следующий вид:
Здесь напряжение
|
|
Рис. 4.1.2.а |
![]()
Ток в цепи определим через напряжение
![]()
![]() А.
А.
Приняв здесь напряжение
![]() В, получаем переходную проводимость
цепи
В, получаем переходную проводимость
цепи![]()
![]() См.
См.
2) Определение импульсных характеристик. Импульсных характеристики определим также, как и в задаче 4.1.1:
![]()
![]()
![]() с-1.
с-1.
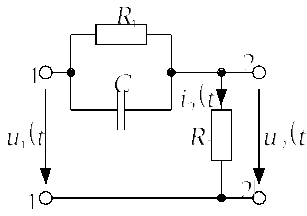
Задача 4.1.3Определить в общем виде
переходную проводимость и переходную
функцию по напряжению![]() для цепи, представленной на рис. 4.1.3.а.
При расчетах учесть, что нагрузка к
зажимам
для цепи, представленной на рис. 4.1.3.а.
При расчетах учесть, что нагрузка к
зажимам![]() не подключена.
не подключена.
|
|
Решение 1) Расчет переходной
проводимости
|
|
Рис. 4.1.3.а |
переходной проводимости найдем ток
![]() и в получившиеся выражение вместо
и в получившиеся выражение вместо![]() подставим единицу. Для этого воспользуемся
операторным методом расчета для чего
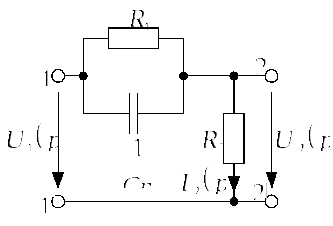
на рис. 4.1.3.Б изобразим операторную схему
замещения. Здесь зажимы
подставим единицу. Для этого воспользуемся
операторным методом расчета для чего
на рис. 4.1.3.Б изобразим операторную схему
замещения. Здесь зажимы![]() разомкнуты (режим холостого хода),
поэтому ток в ветви со входным напряжением
равен току
разомкнуты (режим холостого хода),
поэтому ток в ветви со входным напряжением
равен току![]()
|
|
Найдем
входное операторное сопротивление
Входное напряжение
|
|
Рис. 4.1.3.б |
![]()