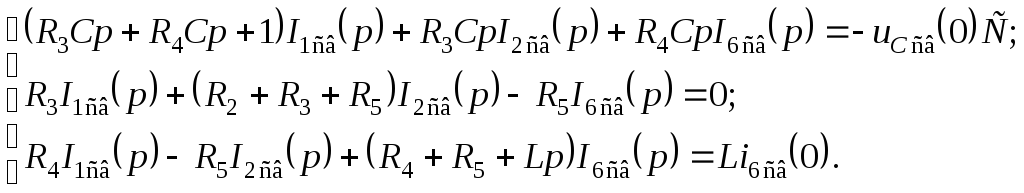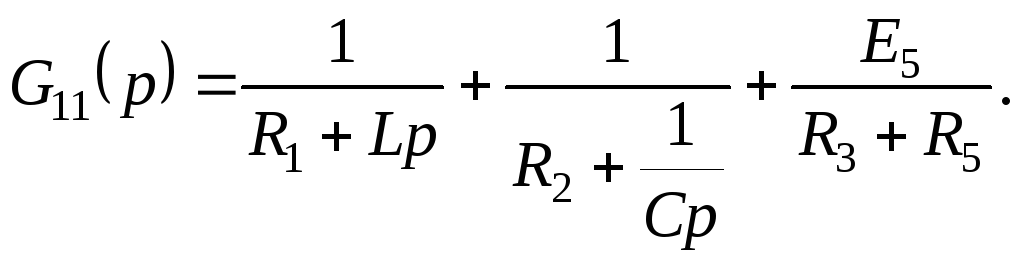По закону Ома для участка цепи определяем искомый операторный ток:

где и– полиномы числителя и знаменателя соответственно,

Для перехода от изображения к оригиналу предварительно найдем корни полинома знаменателя и его производную –

с^-1;

с^-1;

Теперь, зная корни полинома знаменателя, определим искомое выражение для тока источника ЭДС в функции времени:

А.

Здесь введены следующие обозначения:

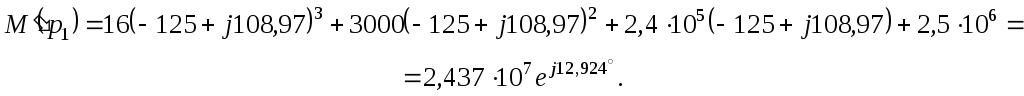
Окончательно запишем найденный операторным методом закон изменения переходного тока

А.

Этот ток совпал с током, найденным в задаче 2.3.11 классическим методом.

Задача 3.2.6Решить задачу 2.3.13 операторным методом.

	Решение Найдем лишь свободные составляющие, а их принужденные составляющие возьмем из задачи 2.3.13. Операторная схема замещения, записанная относительно свободных составляющих, представлена на рис. 3.2.6, для которой А; В. 1) Запишем исходную систему алгебраических уравнений, составленных по
Рис.3.2.6
первому и второму законам Кирхгофа в операторной форме для представленной на рис. 3.2.6 схемы:
		(3.2.1)
		(3.2.2)
		(3.2.3)
		(3.2.4)
		(3.2.5)
		(3.2.6)

Понизим порядок данной системы до третьего. Для этого из уравнений (3.2.1), (3.2.2) и (3.2.3) токи

,иподставим в уравнения (3.2.4), (3.2.5) и (3.2.6) соответственно:

Сделаем группировку слагаемых. В результате получим следующую систему алгебраических уравнений:

или

(3.2.7)

2) Систему уравнений (3.2.7) решим методом Крамера относительно токов и. Сначала найдем главный определитель системы:

Теперь определим искомые изображения токов:

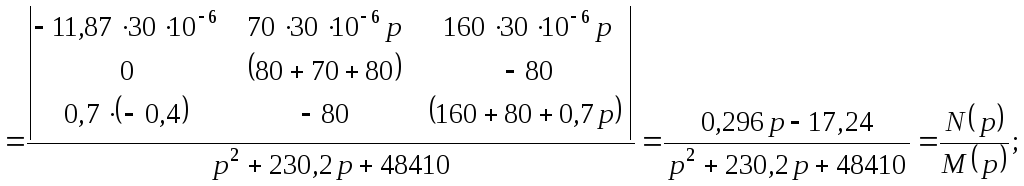
3) Определение оригиналов.

Определим корни полинома знаменателя

откуда

с^-1.

Определим производную полинома знаменателя:

Согласно теореме разложения определим свободный ток в катушке индуктивности в функции времени:

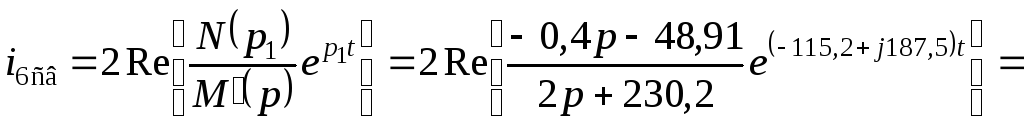
А.

Изображение напряжения на конденсаторе определим как:

Согласно теореме разложения напряжение на емкости

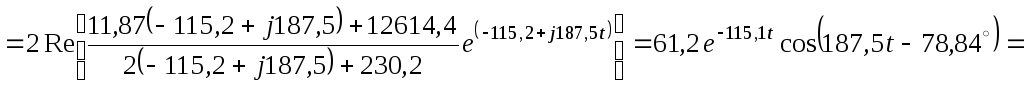
В.

Определим искомые временные функции как сумму принужденных и свободных составляющих:

А;

В.

3.3 Примеры расчета переходных процессов при наличии двух источников энергии

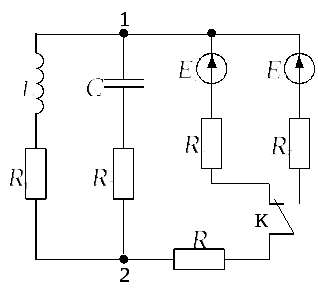
Задача 3.3.1На рис. 3.3.1.а представлена цепь постоянного тока. В момент временипроисходит переключение ключа К с резисторана резисторв следствии чего в цепи начинает происходить переходной процесс. Определить операторное изображение напряжения между узлами “1” и “2”Вычислить значение напряженияв двух точках комплексной плоскостис^-1,с^-1.

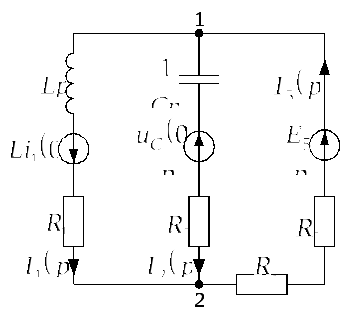
Рис. 3.3.1.а	Рис. 3.3.1.б

Решение

1) Определим независимые начальные условия. Для этого необходима рассчитать цепь до коммутации. На рис. 3.3.1.б начерчена схема, соответствующая работе цепи до коммутации. В данной цепи протекает один постоянный ток через резисторыивеличину которого определим по закону Ома:

А.

Тогда напряжение между обкладками конденсатора определиться как:

В.

На основании законов коммутации получаем следующие начальные условия:

А;

В.

	2) Определение операторного напряжения С этой целью на рис. 3.3.1.а приведена операторная схема замещения исходной цепи. Определим операторное напряжениес помощью метода двух узлов: где
Рис. 3.3.1.в

3) Определим значение напряжения в двух точкахина комплексной области. Для этого подставим выражение дляивместо оператора.

Для с^-1получаем:

См;

Для с^-1получаем:

См;

Итак, получены следующие значения операторного напряжения в точках комплексной плоскостии

Задача 3.3.2 Решить задачу 2.6.3 операторным методом.

	Решение 1) Операторная схема замещения заданной электрической цепи с учетом ненулевых начальных условий (В;) изображена на рис. 3.3.2. 2) Для приведенной операторной схемы замещения составим систему из двух уравнений методом контурных токов: первое уравнение – для контура второе – для контура
Рис. 3.3.2

где

Перенесем слагаемое в правую часть уравнения. Тогда окончательно имеем систему из двух уравнений с двумя неизвестными – операторными контурными токамии

Определяем операторный контурные токи иметодом Крамера:

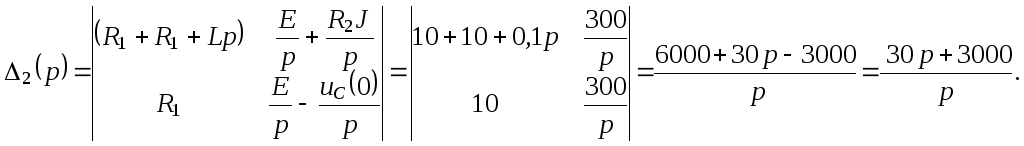
Для нахождения оригиналов предварительно определим корни полинома знаменателя и его производную

с^-1.

Используя теорему разложения, переходим от изображений токов к их временным функциям:

Аналогично находим контурный ток :

с^-1.

Напряжение на конденсаторе в операторной форме можно определить через ток

с^-1.

Задача 3.3.3 В моментпроисходит подключение источника ЭДСВ к цепи, питаемой от источника напряжения с ЭДСВ и представленной на рис. 3.3.3. Найти все переходные токи. Параметры цепи:Ом,мГн,мкФ.

		Решение 1) Для определения независимых начальных условий рассчитаем схему до коммутации . Цепь, соответствующая данному режиму, вычерчена на рис. 3.3.3.б. Ток в конденсаторе и напряжение на индуктивности равен нулю: Тогда имеем:
Рис. 3.3.3.а
Рис. 3.3.3.б	Рис. 3.3.3.в

А;

В.

В итоге получаем следующие независимые начальные условия:

А;

В.

2) Расчет операторных токов.

Операторная схема замещения исходной цепи изображена на рис. 3.3.3.в. Так как в данной схеме три независимых контура и всего два узла, то наиболее целесообразно с точки зрения объема и времени для вычисления операторных токов является метод “двух узлов”.

Найдем операторное выражение напряжения между узлами “2” и “1”:

где

По закону Ома определяем ток

Найдем корни полинома знаменателяи его производную –

c^-1;

с^-1;

По теореме разложения находим временную функцию – ток

А.

Используя закон Ома находим операторный ток

В соответствии с теоремой разложения находим ток

А.

По закону Ома определяем ток в конденсаторе

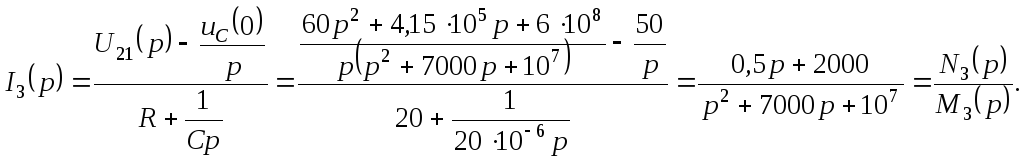
Найдем корни полинома знаменателя и его производную по–

с^-1;

с^-1;

Тогда оригинал этого тока

А.

Рассчитаем операторное изображение тока в катушке индуктивности:

По теореме разложения получаем исходный ток в функции времени:

А.

Проверка:

По первому закону коммутации:

А­ – верно;

По первому закону Кирхгофа для узла “1”:

А – верно.

Задача 3.3.4 Решить задачу 2.6.2 операторным методом.

Решение

Операторным методом рассчитаем только свободные составляющие токов и напряжений, а значения их принужденных составляющих возьмем из решения задачи 2.6.2.

Эквивалентная операторная схема замещения, составленная для свободных составляющих, приведена на рис. 3.3.4.г, для которой

В;

А.

	Для схемы, представленной на рис. 3.4.2.г, составим систему уравнений по первому и второму законам Кирхгофа: Из второго уравнения системы выразим ток в первой ветви
Рис. 3.3.4.г
		(3.3.1)

и подставим в первое уравнение системы, составленное для узла 1 по первому закону Кирхгофа:

отсюда операторный ток конденсатора

(3.3.2)

Подставляя формулы (3.3.2) и (3.3.1) в третье уравнение системы, получим:

откуда операторный ток в катушке индуктивности

Для перехода к оригиналу найдем корни полинома знаменателя:

с^-1,

где корень полинома знаменателякратностью

Тогда полином знаменателя можно представить в виде:

Оригинал найдем по теореме разложения в случае двух одинаковых корней кратностью

Таким образом, ток в катушке

А.

Для нахождения операторного тока в выражение (3.3.2) подставим ток

Оригинал найдем по теореме разложения в случае двух одинаковых корней кратностью

Согласно закону Ома в операторной форме изображение напряжения на конденсаторе

Аналогично найдем временную функцию напряжения на конденсаторе

Итак, напряжение на конденсаторе

В.

Результаты расчетов совпали с расчетами задачи 2.6.2.

3.4 Примеры расчета переходных процессов в цепях третьего порядка

Задача 3.4.1Найти временную функциюсоответствующую операторному изображению по Лапласу

Решение

Представим изображение как отношение полиномов числителя и знаменателя:

Найдем корень полинома знаменателя :

Тогда оригинал найдем в соответствии с теоремой разложения в случае одного нулевого и двух одинаковых корней кратностью

Итак, получен следующий оригинал:

Задача 3.4.2Решить задачу 2.5.1 операторным методом.

Рис. 3.4.2.а	Рис. 3.4.2.б

Исходная цепь вычерчена на рис. 3.4.2.а. Так как в данной цепи нулевые начальные условия, то получаем операторную схему замещения, представленную на рис. 3.4.2.б. Найдем входное операторное сопротивление цепи:

где Ом.

Тогда по закону Ома найдем входной ток – ток в катушке индуктивности

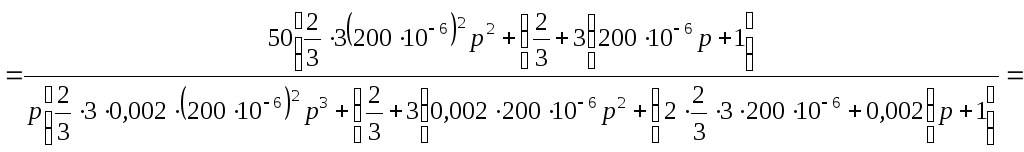
Найдем корни полинома знаменателя и его производную по