С-1; с-1;

По теореме разложения находим закон изменения напряжения на конденсаторе в функции времени –

В.

Итак,

В.

Проверка: подставим в последнее выражение:

Т.е. нулевые начальные условия соблюдаются, значит задача решена верно.

Задача 3.2.2В моментпроисходит подключение пассивного двухполюсника (ПД) с нулевыми начальными условиями, представленного на рис. 3.2.2.а, к источнику синусоидального напряженияВ. При этом в цепи ток источника изменяется по законуА. Найти ток источникапри подключении к этому же двухполюснику источника постоянного напряженияВ. Определить схему и параметры ПД.

	Решение 1) Используя таблицу соответствия между оригиналами и изображениями по Лапласу найдем операторные изображения синусоидального и постоянного источника напряжения а также входного тока ПД
Рис. 3.2.2.а

Тогда определим операторное сопротивление ПД:

2) Определим операторный ток при включении источника постоянного напряжения:

Определим корни полинома знаменателя

с^-1.

Прейдем от операторного изображения этого тока к его оригиналу по формуле разложения:

А,

где производная полинома знаменателя по

3) Определение параметров ПД. Так как по условию задачи на схему воздействует синусоидальное напряжение с начальной фазой и принужденный ток от этого воздействия имеет начальную фазузначит сдвиг фаз между ними

Следовательно, входное сопротивление ПД носит активно – индуктивный характер.

Используя найденный входной ток определим параметры ПД. Его значение прине равно нулю:

А.

Найденный ток имеет один корень отрицательный корень характеристического уравненияс^-1, значит ПД имеет лишь один накопитель энергии – катушку индуктивности. Кроме того по условию задачи имеются нулевые начальные условия, т.е. ток в катушке в момент коммутации равен нулю. Учитывая приведенные в пункте 3 рассуждения выберем схему ПД, как показано на рис. 3.2.2.б.

	При на основании закона Ома можно записать: следовательно Ом. В установившимся режиме когда токА катушка закорочена, поэтому
Рис. 3.2.2.б

Ом.

Используя ранее составленное соотношение находим сопротивление резистора

Ом.

	Операторная схему замещения ПД при воздействии на него постоянного напряжения изображена на рис. 3.2.2.в. Запишем Закон Ома в операторной форме для этой схемы при Запишем условие равенства полинома знаменателя нулю:
Рис. 3.2.2.в

При известном корне с^-1полиномесли

Тогда

Гн.

Задача 3.2.3 Решить задачу 2.6.2 операторным методом.

	Решение Найдем только свободные составляющие искомых временных функций, а их полные решения представим в виде суммы принужденных и свободных составляющих. При этом принужденные составляющие возьмем из решения задачи 2.6.2. Операторная схема замещения приведена на рис. 3.2.3, для которой А;
Рис. 3.2.3

В.

1) Составляем исходную систему из трех алгебраических уравнений, составленных по первому и второму законам Кирхгофа:

Решим эту систему уравнений методом Крамера, для чего определим главный определитель и его алгебраические дополнения:

Тогда операторный ток

Определим корни полинома знаменателя и его производную –

с^-1;

По теореме разложения определяем временную функция этого тока:

Найдем операторное напряжение . Так как по закону Ома

то второе уравнение исходной системы уравнений можно записать следующим образом:

откуда

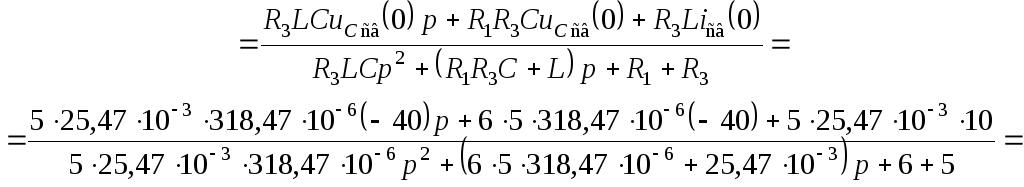
По теореме разложения определяем оригинал –

В.

Теперь запишем полные временные функции:

А;

В.

Задача 3.2.4 Цепь, представленная на рис. 3.2.4.а, питается от источника синусоидального напряжения с ЭДСВ (частотас^-1). В моментпроисходит замыкание ключа К, в результате которого шунтируется резисторОпределить ток в индуктивностии напряжение на конденсатореесли заданы следующие параметры цепи:Ом,Ом,Ом,Ом,Ф.

Рис. 3.2.4.а	Рис. 3.2.4.б

Решение

Расчет будем вести для свободных составляющих, а принужденные составляющие рассчитаем символическим методом.

Определим реактивные сопротивления приемников:

Ом;

Ом.

1) Рассчитаем схему до коммутации с целью определения независимых начальных условий. Эта схема изображена на рис. 3.2.4.б. Воспользуемся символическим методом и найдем комплексное эквивалентное сопротивление:

Ом.

По закону Ома определяем комплекс тока в ветви с источником ЭДС:

А.

Найдем комплекс напряжения между обкладками конденсатора:

В.

Перейдем от комплексных изображений к оригиналам:

А;

В.

На основании законов коммутации получаем следующие независимые начальные условия:

А;

В.

	2) Послекоммутационная схема приведена на рис. 3.2.4.в. Расчет этой схемы аналогичен расчету цепи, представленной на рис. 3.2.4.б: Ом; А;
Рис. 3.2.4.в

В.

Тогда запишем временные функции:

А;В.

	3) Операторная схема замещения вычерчена на рис. 3.2.4.г, для которой имеем: В. Для схемы, приведенной на рис. 5.2.4.г, составляем исходную систему из трех
Рис. 3.2.4.г

алгебраических уравнений в соответствии с законами Кирхгофа:

Решим эту систему уравнений методом Крамера, для чего определим главный определитель и его алгебраические дополнения:

Тогда операторные токи

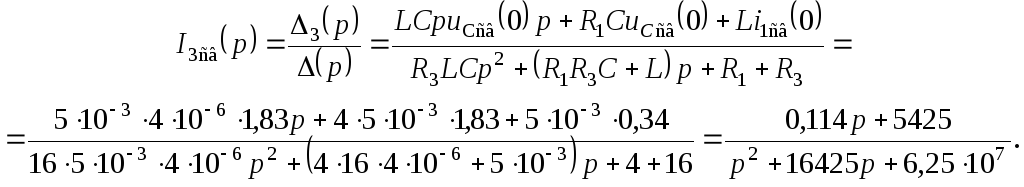
По закону Ома операторное напряжение

Определим корни полинома знаменателяи его производную –

с^-1;

с^-1;

По теореме разложения определяем искомые временные функции:

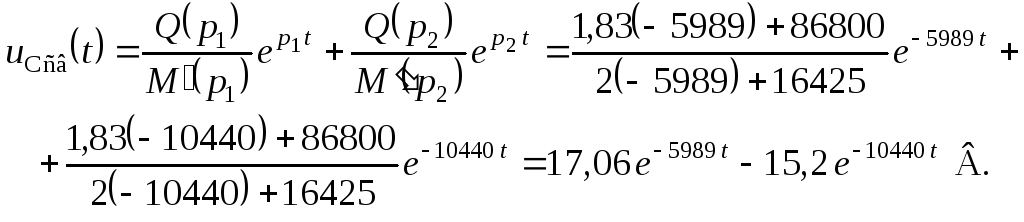
Теперь запишем полные временные функции:

А;

В.

Проверка: при получаем:

А;

В,

Эти значения соответствуют независимым начальным условиям, что говорит о достоверности полученных результатов.

Задача 3.2.5Решить задачу 2.3.11 операторным методом.

	Решение 1) Операторная схема замещения приведена на рис. 3.2.5, для которой – начальное значение тока в катушке индуктивности, А; – изображение по Лапласу синусоидальной ЭДСопределяемое по таблицам соответствия оригиналов и изображений, 2) Операторный ток легче всего
Рис. 3.2.5

найти используя метод “двух узлов”. Для этого найдем операторное напряжение между узлами “2” и “1” – , и затем по закону Ома найдем искомый операторный ток.

Согласно указанному алгоритму определяем узловое напряжение , положительное направление которого показано на рис. 3.2.5: