Решение

Операторная схема замещения представлена на рис. 3.1.7.б, в которой ток в катушке А в соответствии с докоммутационной схемой.

1) Составим исходную систему из двух алгебраических уравнений согласно схеме на рис. 3.1.7.б: первое – по первому закону

Сгруппируем слагаемые во втором уравнении системы:

Теперь подставим сюда операторный ток выраженный из первого уравнения исходной системы:

Откуда

Для нахождения оригинала найдем корень полинома знаменателя

с^-1.

Найдем производную

По теореме разложения находим оригинал

А.

Определим по закону Кирхгофа операторный ток

Определим временную функцию тока согласно теореме разложения:

А.

Задача 3.1.8Решить задачу 2.7.1.

	Решение Операторная схема замещения представлена на рис. 3.1.8., в которой А (см. задачу 2.7.1) На основании закона Ома в операторной форме находим операторный ток Для нахождения оригинала найдем корни полинома знаменателя: с-1.
Рис. 3.1.8

Найдем производную полинома знаменателя:

В соответствии с теоремой разложения находим оригинал тока

А.

По закону Ома рассчитаем напряжение

По теореме разложения переходим от изображения к оригиналу – временной функции

В.

Задача 3.1.9 Решить задачу 2.4.2.

Решение Операторная схема замещения вычерчена на рис. 3.1.9.б с учетом встречного включения катушек. Здесь А. 2) Для операторной схемы замещения составляем исходную систему из трех уравнений, учитывая встречное включение катушек: первое – по первому закону Кирхгофа для узла “1”, второе – по второму закону для контура, содержащего источник ЭДС и катушку с индуктивностью третье – по второму закону Кирхгофа для замкнутого контура, содержащего катушки с индуктивностямии

Рис. 3.1.9.а

Определяем операторный токи иметодом Крамера:

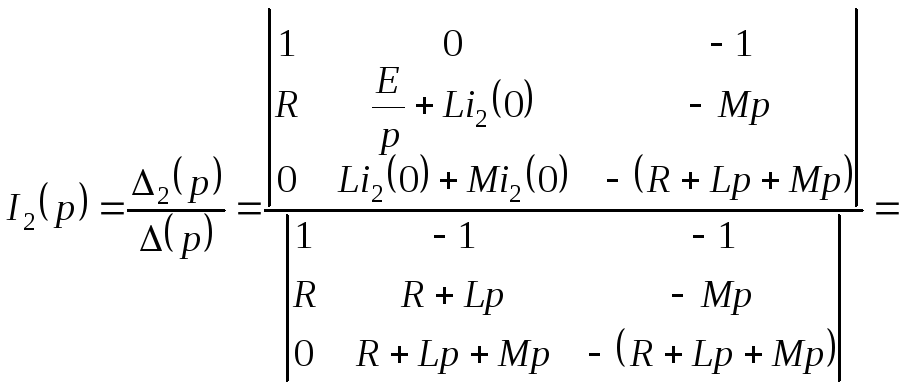
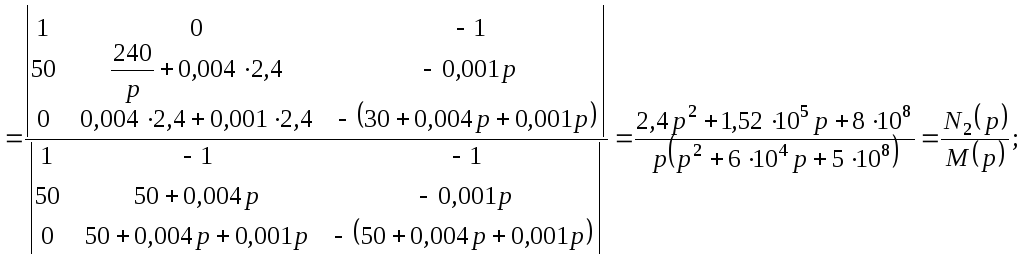
Для нахождения оригиналов предварительно определим корни полинома знаменателя и его производную

с^-1;

с^-1;

Используя теорему разложения переходим от изображений токов к их временным функциям:

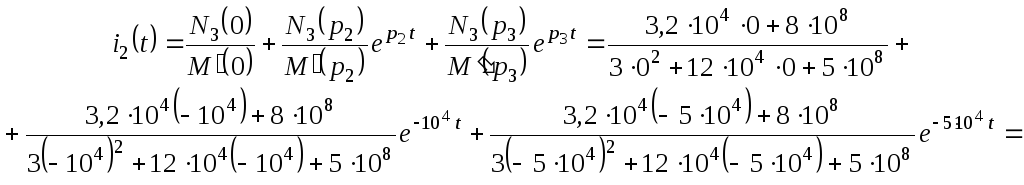
А;

А.

Окончательно запишем полученные временные функции токов:

А;

А.

Задача 3.1.10 Построить операторную схему замещения цепи с ненелевыми начальными условиями, изображенной на рис.3.1.10.а.

	Решение Для заданной цепи составим систему из двух уравнений по второму закону для двух независимых контуров, учитывая встречное включение индуктивно связанных катушек: Теперь перейдем от мгновенных значений токов и напряжений к их операторным изображениям по Лапласу. При этом будем иметь в виду ненулевые начальные условия, т.е. для данной схемы это значения токов иТогда получим следующие алгебраические уравнения: Или
Рис. 3.1.10.а
Рис. 3.1.10.б

По последним двум выражениям на рис. 3.1.10.б составлена операторная схема замещения.

3.2 Примеры расчета переходных процессов в цепях переменного тока

Задача 3.2.1В Цепи, представленной на рис. 3.2.1.а, в моментзамыкается ключ К и подключается источник синусоидального напряжения с ЭДСВ. Найти выражение напряжения на конденсатореИзвестно:В,с^-1,Ом,Ом,мкФ.

	Решение 1) В цепи нулевые начальные условия: Тогда операторная схема замещения примет вид, как показано на рис. 3.2.1.б. Здесь изображение синусоидальной ЭДС с начальной фазойимеет вид: Операторное изображение входного тока определим с помощью закона Ома, составленного в операторной форме:
Рис. 3.2.1.а
Рис.3.2.1.б

Тогда операторное изображение напряжение между обкладками конденсатора определим как произведение входного операторного тока на эквивалентное операторное сопротивление между узлами “1” и “2” –

Для нахождения оригинала напряжения на конденсаторе найдем корни полинома знаменателя и его производную: