- •Министерство образования и науки Российской Федерации
- •Введение
- •Перечень условных обозначений
- •1 Основные теоретические положения
- •1.1. Физические основы переходных процессов
- •1.2 Математический аппарат и алгоритмы расчетов
- •1.2.1 Классический метод анализа переходного процесса
- •1.2.2 Операторный метод расчета (метод преобразования Лапласа)
- •1.2.3 Расчет методом интеграла Дюамеля
- •1.2.4 Метод переменных состояния переходных процессов
- •2 Классический метод расчета переходных процессов в линейных электрических цепях
- •2.1 Примеры расчета переходных процессов в цепях с индуктивностью
- •Имеет один отрицательный и действительный корень
- •Решение
- •И подставим его в первое уравнение системы:
- •Источника напряжения
- •Получим характеристическое уравнение
- •Решение
- •Первый способ
- •Решение
- •Ом; Ом.
- •Решение
- •Решение
- •И падение напряжение на индуктивности
- •Решение
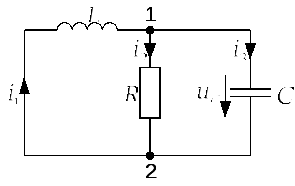
- •Поэтому в соответствии с первым законом Кирхгофа для узла “1” ток в индуктивности, питаемый источником тока равен току в ветви с резистором: а.
- •Откуда составляем характеристическое уравнение:
- •Где ток в конденсаторе.
- •Отсюда находим характеристическое уравнение:
- •С-1; с-1.
- •С-1; с-1.
- •Решение
- •Напряжение между узлами 1 и 2 определяется как:
- •И подставим туда ток конденсатора (2.6.6):
- •Откуда характеристическое уравнение оду будет иметь вид:
- •2.8 Задачи для самостоятельного решения
- •3 Операторный метод расчета переходных процессов в линейных электрических цепях
- •3.1 Примеры расчета переходных процессов в цепях постоянного тока
- •Решение
- •Решение
- •3.2 Примеры расчета переходных процессов в цепях переменного тока
- •С-1; с-1;
- •По закону Ома для участка цепи определяем искомый операторный ток:
- •С-1; с-1;
- •4 Расчет переходных процессов с помощью интеграла дюамеля
- •4.1 Примеры расчета переходных и импульсных характеристик
- •Тогда по закону Ома в операторной форме определяем ток
- •Решение
- •С-1; с-1;
- •4.2 Примеры расчета переходных процессов с помощью интеграла Дюамеля
- •Решение
- •4.3 Задачи для самостоятельного решения
- •5 Расчет переходных процессов методом переменных состояния
- •5.1 Примеры расчета
- •Определим собственные значения матрицы a, т.Е. Корни уравнения
- •. Определим собственные значения матрицы a, т.Е. Корни уравнения
- •5.2 Задачи для самостоятельного решения
- •Список литературы
- •Содержание
- •Часть II
- •190008, Г.С.-Петербург, ул. Лоцманская, 3.
Решение
1) Схема до коммутации
![]() представлена на рис. 2.3.5.б. Постоянный
ток через конденсатор не течет:
представлена на рис. 2.3.5.б. Постоянный
ток через конденсатор не течет:
![]()
Поэтому в соответствии с первым законом Кирхгофа для узла “1” ток в индуктивности, питаемый источником тока равен току в ветви с резистором: а.
По закону Ома определим напряжение на конденсаторе:
![]() В.
В.
|
|
|
|
Рис. 2.3.5.в |
Рис. 2.3.5.д |
2) Схема после коммутации
![]() изображена на рис. 2.3.5.в. Принужденные
составляющие в этой цепи равны нулю,
так как в этой схеме нет источников
вынуждающей силы (источников ЭДС и
источников тока).
изображена на рис. 2.3.5.в. Принужденные
составляющие в этой цепи равны нулю,
так как в этой схеме нет источников
вынуждающей силы (источников ЭДС и
источников тока).
3) Цепь в момент коммутации
![]() приведена на рис. 2.3.5.д. Для определения
переходного процесса составляем систему
из трех уравнений: первое – по первому
закону Кирхгофа для узла “1”, второе –
по второму закону Кирхгофа для внешнего
контура
приведена на рис. 2.3.5.д. Для определения
переходного процесса составляем систему
из трех уравнений: первое – по первому
закону Кирхгофа для узла “1”, второе –
по второму закону Кирхгофа для внешнего
контура![]() третье – по второму закону Кирхгофа
для контура
третье – по второму закону Кирхгофа
для контура![]()

где
![]()
Записанную систему уравнений решим
относительно напряжения на конденсаторе
![]() так как для него выполняется второй
закон коммутации – запрет скачка
напряжения.
так как для него выполняется второй
закон коммутации – запрет скачка
напряжения.
Из третьего уравнения системы выразим ток в ветви с резистором:
![]()
Теперь подставим этот ток и ток в
конденсаторе
![]() в первое уравнение исходной системы:
в первое уравнение исходной системы:
|
|
(2.3.1) |
Наконец, сделаем подстановку последнего тока (2.3.1) во второе уравнение системы:
![]()
После преобразований окончательно получаем НДУ второго порядка:
![]()
которое ввиду равенства нулю его правой части совпадает с ОДУ
![]()
Из последнего выражения составим характеристическое уравнение:
![]()
или
![]()
![]()
![]()
Характеристическое уравнение имеет два отрицательных, вещественных корня:
![]() с-1;
с-1;
![]() с-1.
с-1.
В случае двух различных отрицательных корней общее решение ОДУ имеет вид:
|
|
(2.3.2) |
Постоянные интегрирования
![]() и
и![]() определим следующим образом.
определим следующим образом.
Подставим ОДУ (2.3.2) в (2.3.1):
![]()
Переписав (2.3.2) и последнее выражение получим следующую систему уравнений:

Запишем эту систему при
![]()

Учитывая, что в соответствии с законами коммутации ток в катушке индуктивности и напряжение на конденсаторе не могут изменяться скачком, т.е.
![]() А;
А;
![]() В,
В,
последняя система уравнений преобразуется к виду:
|
|
(2.3.3) |
Выразив из первого уравнения системы (2.3.3) постоянную интегрирования
![]()
и подставив во второе уравнение системы (4.3.3), получим
![]()
![]()
Подставив найденные постоянные
интегрирования и корни характеристического
уравнения
![]() и
и![]() в НДУ (2.3.2), получим искомое напряжение
на конденсаторе:
в НДУ (2.3.2), получим искомое напряжение
на конденсаторе:
![]() В.
В.
3) Определяем остальные токи, используя приведенные выше соотношения:
|
|
Графики требуемых временных функций приведены на рис. 2.3.5.г. |
|
Рис. 2.3.5.г |
Задача 2.3.6Цепь, изображенная на
рис. 2.3.6.а, в момент![]() подключается к источнику постоянной
ЭДС
подключается к источнику постоянной
ЭДС![]() В путем замыкания рубильника Р.
Параметры цепи:
В путем замыкания рубильника Р.
Параметры цепи:![]() Ом,
Ом,![]() Ом,
Ом,![]() мГн,
мГн,![]() мкФ. Найти ток в катушке индуктивности
мкФ. Найти ток в катушке индуктивности![]() и напряжение на конденсаторе
и напряжение на конденсаторе![]()
|
|
|
|
Рис. 2.3.6.а |
рис. 2.3.6.б |
Решение
1) Так как до коммутации
![]() в цепи не было источника ЭДС
в цепи не было источника ЭДС![]() то напряжение на конденсаторе и ток в
индуктивности равны нулю:
то напряжение на конденсаторе и ток в
индуктивности равны нулю:
![]()
![]()
Используя первый и второй законы коммутации, получаем следующие независимые начальные условия:
![]()
![]()
2) Схемы после коммутации
![]() вычерчена на рис. 2.3.6.б. Ток через
заряженный конденсатор равен нулю
(
вычерчена на рис. 2.3.6.б. Ток через
заряженный конденсатор равен нулю
(![]() ),поэтому
согласно закону Ома для узла “1” ток
источника ЭДС равен току во второй
ветви:
),поэтому
согласно закону Ома для узла “1” ток
источника ЭДС равен току во второй
ветви:
![]()
Тогда в данной цепи имеется один замкнутый
контур
![]() в котором протекает ток
в котором протекает ток
![]() А.
А.
По закону Ома находим напряжение
![]()
![]() В.
В.
3) Для схемы, изображенной на рис. 2.3.6.а,
в момент коммутации
![]() при замыкании рубильника Р составляем
исходную систему из трех уравнений:
первое – по первому закону Кирхгофа
для узла “1”, второе – по второму закону
Кирхгофа для контура
при замыкании рубильника Р составляем
исходную систему из трех уравнений:
первое – по первому закону Кирхгофа
для узла “1”, второе – по второму закону
Кирхгофа для контура![]() третье – на основании второго закона
Кирхгофа для контура
третье – на основании второго закона
Кирхгофа для контура![]()
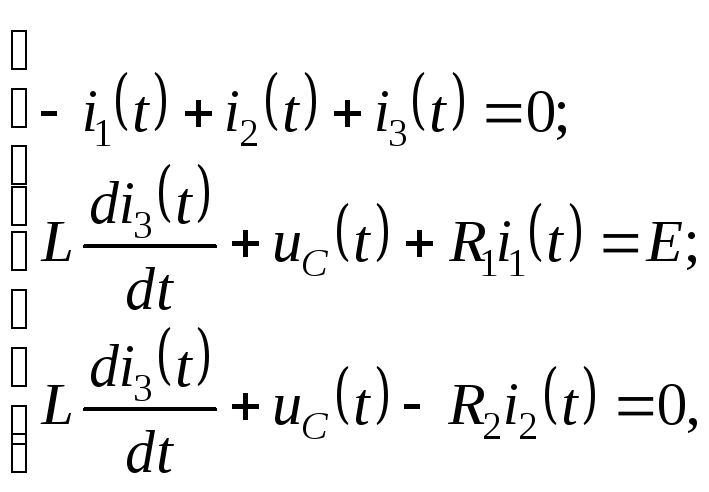
где
![]() – ток. в конденсаторе и одновременно в
катушке индуктивности,
– ток. в конденсаторе и одновременно в
катушке индуктивности,
|
|
(2.3.4) |
Выразим ток
![]() из второго уравнения системы, и ток
из второго уравнения системы, и ток![]() из третьего уравнения исходной системы:
из третьего уравнения исходной системы:


Теперь подставим эти токи в первое уравнение системы:

Умножив обе части данного уравнения на
![]() и сгруппировав слагаемые, получим
и сгруппировав слагаемые, получим
![]()
Подставив ток (2.3.4) в последнее уравнение, получаем НДУ второго порядка:
![]()
![]()
![]()
Приравняв правую часть НДУ, получаем ОДУ:

Тогда получим следующее характеристическое уравнение:
![]()
![]()
![]()
Данное уравнение имеет два отрицательных и вещественных корня:
![]() с-1;
с-1;
![]() с-1.
с-1.
НДУ для напряжения
![]() в случае двух отрицательных действительных
корней имеет общее решение следующего
вида:
в случае двух отрицательных действительных
корней имеет общее решение следующего
вида:
|
|
(2.3.5) |
Постоянные интегрирования
![]() и
и![]() определим с помощью уравнений (2.3.4),
(2.3.5) и независимых начальных условий.
определим с помощью уравнений (2.3.4),
(2.3.5) и независимых начальных условий.
Для этого подставим в соотношение (2.3.4) выражение (2.3.5):
![]()
Составим систему из выражения (2.3.4) последнего уравнения:

При
![]() имеем:
имеем:

Используя независимые начальные условия,
окончательно получим систему из двух
уравнений с двумя неизвестными
![]() и
и![]()

Путем подстановки из первого уравнения
последней системы
![]() во второе уравнение находим постоянные
интегрирования:
во второе уравнение находим постоянные
интегрирования:
![]()
![]()
Итак, напряжение на конденсаторе
![]() В.
В.
Ток в катушке индуктивности
![]() определим путем подстановки найденного
напряжения
определим путем подстановки найденного
напряжения![]() в формулу (2.3.4):
в формулу (2.3.4):
![]()
![]() А.
А.
Задача 2.3.7В цепи, изображенной на
рис. 2.3.7.а, в момент![]() замыкается ключ К и подключается источник
постоянного напряжения
замыкается ключ К и подключается источник
постоянного напряжения![]() В. Найти все токи и напряжение на
конденсаторе. Даны следующие параметры
цепи:
В. Найти все токи и напряжение на
конденсаторе. Даны следующие параметры
цепи:![]() Ом,
Ом,![]() Ом,
Ом,![]() мГн,
мГн,![]() мкФ.
мкФ.
|
|
|
|
Рис. 2.3.7.а |
рис.2.3.7.б |
Решение
1) Так как до коммутации
![]() в цепи не было источника напряжения
в цепи не было источника напряжения![]() значит напряжение на конденсаторе и
ток в индуктивности равны нулю:
значит напряжение на конденсаторе и
ток в индуктивности равны нулю:
![]()
![]()
Используя первый и второй законы коммутации, получаем следующие независимые начальные условия:
![]()
![]()
2) Схема после коммутации
![]() приведена на рис. 4.3.7.б. Сопротивление
конденсатора постоянному току равно
бесконечности
приведена на рис. 4.3.7.б. Сопротивление
конденсатора постоянному току равно
бесконечности
![]()
следовательно, ток
![]()
Падение напряжения от постоянного тока на индуктивном элементе также равно нулю:
![]()
Значит по первому закону Кирхгофа для узла “1” ток в катушке индуктивности равен току источника напряжения:
![]() А.
А.
По закону Ома напряжение на конденсаторе определяется падением напряжения от действия тока в катушке индуктивности:
![]() В.
В.
3) Для схемы, приведенной на рис. 2.3.7.а, в
момент подключения источника напряжения
![]() к цепи
к цепи![]() составляем исходную систему из трех
уравнений: первое – по первому закону
Кирхгофа для узла “1”, второе – по
второму закону Кирхгофа для контура
составляем исходную систему из трех
уравнений: первое – по первому закону
Кирхгофа для узла “1”, второе – по
второму закону Кирхгофа для контура![]() третье – в соответствии со вторым
законам Кирхгофа для контура
третье – в соответствии со вторым
законам Кирхгофа для контура![]()
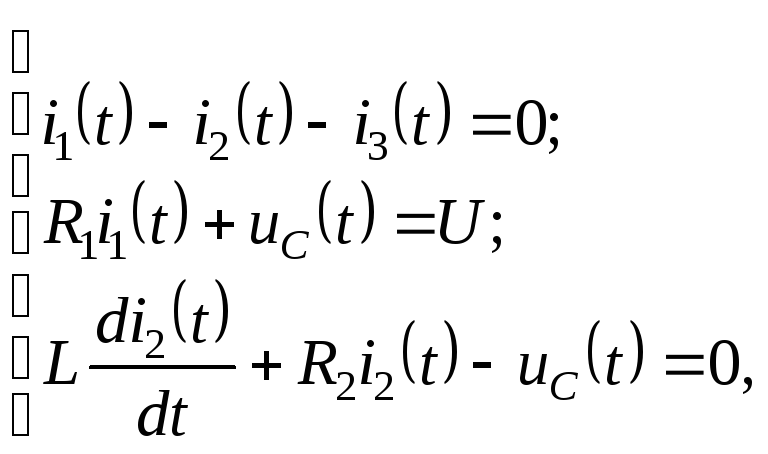
где
![]()
Решим эту систему уравнений относительно
напряжения
![]() способом подстановки.
способом подстановки.
Из второго уравнения системы определим
ток
![]()
![]()
Подставим в первое уравнение системы
последний ток и ток в конденсаторе
![]()
![]()
Тогда определяем ток в катушке индуктивности через напряжение на емкости:
|
|
(2.3.6) |
Наконец, подставим (2.3.6) в третье выражение исходной системы уравнений:

Умножив правую и левую части последнего
выражения на
![]() и сгруппировав слагаемые, получим НДУ
второго порядка:
и сгруппировав слагаемые, получим НДУ
второго порядка:
![]()
Приравняв правую часть данного НДУ к нулю, получим ОДУ:
![]()