4.4. Построение функции принадлежности

Существующие методы построения по экспертным оценкам функции принадлежности нечеткого множества можно разделить на два вида: прямые и косвенные. Прямые методы характеризуются тем, что эксперт непосредственно задает правило определения значений функции принадлежности _A, характеризующей понятиеА. Эти значения согласуются с его предпочтениями на множестве объектов следующим образом:

• для любых

тогда и только тогда, когда u₂предпочтительнееu₁;

• для любых

тогда и только тогда, когда u₁иu₂безразличны относительно понятияА.

В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворить заранее сформулированным условиям. Экспертная информация является исходной информацией для дальнейшей обработки. При вычислении функции принадлежности могут налагаться дополнительные условия, например, функция принадлежности должна отражать близость к заранее выявленному эталону, если при попарном сравнении один объект оценивается в раз сильнее, чем другой, то второй объект оценивается в1/раз сильнее, чем первый и др.

Рассмотрим, одни из прямых методовопределения функции принадлежности_A(u)элементовuUк нечеткому множествуА. Пусть имеется некоторое число экспертов; часть из них на вопрос о принадлежности элементаu. к множествуАотвечают положительно (обозначим это число какn₁), другая часть ‑ отрицательно (их число –n₂). Тогда

.

Для вычисления функции принадлежности Т. Саати [3] предложил следующий метод (косвенный), основанный на матрице парных сравнений.Впоследствии этот подход оформился в целый раздел принятия решений при наличии одного, а также нескольких критериев и получил наименование метода анализа иерархий (the Analytic Hierarchy Process, AHP); сокращенно МАИ. В практике часто имеют место случаи, когда не существует элементарных измеримых свойств, признаков, через которые определяются интересующие понятия, например, красота, интеллектуальность. В таких случаях трудно оценить степень проявления свойства у рассматриваемого объекта. Степени принадлежности рассматриваются на данном реальном множестве, а не в абсолютном смысле. Поэтому интенсивность принадлежности можно определить, исходя из попарных сравнений рассматриваемых элементов. Если обозначить степень принадлежности как

(n‑ число точек, в которых сравниваются значения функции принадлежности), то можно построить матрицуэлементы которой

означают, по мнению эксперта, во сколько раз w_iбольшеw_j. Имея матрицу попарных сравненийA, можно вычислить значения.

Функции принадлежности определяются как решение задачи поиска собственного вектора матрицыA, соответствующего максимальному собственному числуматрицыA

. (15)

Значение функции принадлежности определяются по формуле

(16)

Чем ближе к числуn, тем более верным является результат.

Так как задача (15) имеет неединственное решение, то значение функции принадлежности определяется согласно (16).

В табл. 8 указаны качественные оценки и численные значения e_ij, которые можно использовать при опросе эксперта.

Однако, такой способ построения функции принадлежности из-за нарушения на практике свойства совместности (consistency) [3], [4] матрицы парных сравнений не является обоснованным. Известно, что при формировании в соответствии с МАИ экспертами матрицы парных сравнений рассчитывать на ее совместность не следует. Тем не менее, согласно МАИ, весовой вектор вновь предлагается находить как собственный вектор (несовместной) матрицы парных сравнений. Причем этот собственный вектор отвечает собственному значению, которое, уже не равно (а строго больше)n. В обширной литературе по МАИ не существует (по крайней мере, на данный момент) доказательства того, что искомый весовой вектор необходимо должен являться собственным вектором несовместной матрицы, отвечающим ее максимальному собственному значению, большему, чемn. По этой причине рассматриваемый метод нельзя назвать обоснованным. Он представляет собой определенный эвристический подход, логика которого заключается в рекомендации действовать точно так же в ситуациях, которые могут сильно отличаться от тех, для которых установлена справедливость данных действий. Это означает, что применение МАИ практически всегда содержит некоторую «модельную» ошибку вычисления весового вектора (помимо погрешностей чисто вычислительного характера) и если эта ошибка велика, то применение МАИ становится просто неприемлемым. Отдавая себе отчет в этом, автор МАИ ввел специальный числовой показатель «индекс совместности» (consistencyindex), характеризующий степень доверия к полученным с помощью МАИ результатам. Этот индекс трактуется как своеобразная мера отклонения исходной несовместной матрицы от некоторой совместной. Как указывает Т. Саати, при достаточно малом значении индекса совместности матрица парных сравнений «близка» к некоторой матрице с нулевым значением этого индекса (т.е. к некоторой совместной матрице). Тем самым, и результат применения МАИ в виде весового вектора оказывается в какой-то мере «близким» к результату, получаемому на основе этой совместной матрицы. Если же индекс совместности превышает «пороговое» значение, то сделать вывод о близости указанных матриц нельзя, поэтому и применять МАИ в таких случаях автором не рекомендуется. Следует, однако, заметить, что по значению индекса совместности можно лишь опосредованно судить о величине итоговой «модельной» ошибки; точно она никогда и никем не может быть определена. Такова специфика данного эвристического подхода.

В связи с вышеизложенным, был предложен упрощенный вариант метода анализа иерархий [5]. В этом методе процедуру формирования матрицы парных сравнений предлагается существенно упростить, требуя от эксперта сведения не обо всех элементах этой матрицы, расположенных выше (либо ниже) главной диагонали, а лишь об определенных «базисных» элементах, на основе которых затем легко и без ошибок вычислительного характера находится искомый весовой вектор. При этом выбор конкретного «базисного» набора соответствует той или иной схеме сравнения объектов, которую можно выбирать с целью получения наиболее надежных результатов от эксперта. В целом предлагаемый вариант оказывается существенно проще исходного метода как на стадии формирования матрицы E, так и в ходе вычисления весового вектора. Кроме того, он полностью избавлен от «модельной» ошибки, о которой шла речь выше, поскольку основан на совместной матрице E.

Пусть имеется набор nобъектовA₁,A₂,...,A_nи задача состоит в определении веса каждого из них, т.е. в нахождении соответствующих им положительных чиселw_l,w₂,...,w_n.

Будем считать, что матрица парных сравнений должна обладать всеми свойствами матрицы относительных весов (т.е. быть совместной). В соответствии с этим потребуем:

1. Все элементы матрицы Aположительны:для всех номеров

2. Матрица Aобратно симметрична:для всех номеровВ частности,

3. Матрица Aсовместна, т.е. равенствоимеет место для всех номеров

4. Число nявляется максимальным собственным значением матрицыAи для некоторого единственного (нормированного) вектор-столбцас положительными компонентами выполняется равенство.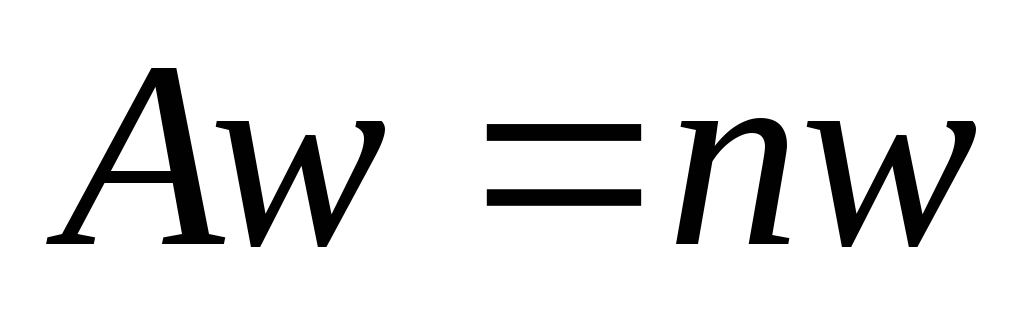

Построение матрицы парных сравнений на основе элементов первой строки. В силу первых двух свойств, перечисленных выше, диагональные элементы матрицы парных сравнений известны ‑ это единицы. Далее эксперту предлагают сравнить вес первого объекта с весом второго объекта и указать положительное число, показывающее во сколько раз вес первого объекта больше веса второго объекта. В результате выполнения такого сравнения эксперт назначает некоторое положительное число a₁₂. Далее для сравнения с первым объектом рассматривается третий объект и в результате сравнения экспертом указывается числоa₁₃, и т.д. После выполнения сравнений первого объекта со всеми остальными будут назначены положительные числа. Тем самым, с учетом равенствабудет известна вся первая строка матрицыА. Описанный способ назначения элементов первой строки матрицыАможно назвать «схемой сравнения с образцом», в роли которого выступает первый объект.

Остальные элементы матрицы парных сравнений можно найти на основе свойств 2 и 3 матрицы парных сравнений. Благодаря этим свойствам имеют место равенства

(17)

с помощью которых однозначно вычисляются элементы остальных строк матрицы А. Заметим, что равенство (17) выполняется и для элементов первой строки, т.е. приi= 1.

Нетрудно видеть, что матрица А, построенная на основе элементов первой строки согласно формуле (17), будет удовлетворять свойству совместности, так как для всех номероввыполнено

.

Нахождение весового вектора. После того как матрица при помощи формулы (17) сформирована, можно найти весовой вектор. Его компоненты вычисляются по формуле

(18)

Вектор весов w, вычисленный согласно (18), не удовлетворяет требованию нормировки, так как его последняя компонента равна единице. Если необходимо, чтобы он был нормирован, каждую его компоненту следует разделить на сумму всех компонент, т.е. на величину, где все слагаемые, найдены по формуле (18).

Замечание. Компоненты весового вектораw, найденного с помощью (18), составляют последний столбец матрицыА, элементы которой построены на основе формулы (17).

Способы построения функций принадлежности, естественно, не исчерпываются изложенным. Выбор определенного метода должен обуславливаться конкретной задачей.