
- •Введение
- •Лекция 1. Основные положения теории принятия решений
- •1.1. Определения
- •1.2. Этапы принятия решений
- •1.3. Формулирование проблемы
- •1.4. Выявление целей
- •1.5. Формирование критериев
- •1.6. Генерирование альтернатив
- •1.7. Основные понятия лекции №1
- •Литература
- •Лекция 2. Классификация задач принятия решений и методов их решения
- •2.1. Классификационное дерево задач принятия решений (зпр) и методов их решения
- •2.2. Общая постановка однокритериальной задачи принятия решения
- •2.3. Общая формулировка задачи со стохастической неопределенностью
- •2.4. Основные понятия лекции №2
- •Литература
- •Лекция 3. Задачи и методы критериального выбора
- •3.1. Классификация задач и методов критериального выбора
- •3.2. Поиск альтернативы с заданными свойствами
- •3.3. Отбор недоминируемых альтернатив
- •3.4. Принцип справедливой уступки
- •3.4.1. Принцип абсолютной уступки
- •3.4.2. Принцип относительной уступки
- •3.5. Приоритет важнейшего критерия
- •3.5.1. Условная максимизация с ограничениями по равенству
- •3.5.2. Условная максимизация с ограничениями по неравенству
- •3.5.3. Метод уступок
- •3.6. Сведение многокритериальной задачи к однокритериальной
- •3.7. Способы нормализации локальных критериев
- •3.8. Способы задания и учета приоритета локальных критериев
- •3.9. Пример многокритериальной задачи принятия решений
- •3.10. Основные понятия лекции №3
- •Литература
- •Лекция 4. Задачи Принятия решений в условиях неопределнности
- •4.1. Схема оптимизационного исследования в условиях неопределенности
- •4.2. Нечеткие модели оптимизации
- •4.2.1.Элементы теории нечетких множеств
- •4.2.2. Лингвистические переменные
- •4.3. Шкала отношений и матрицы парных сравнений
- •4.4. Построение функции принадлежности
- •4.5. Многокритериальный выбор альтернатив на основе пересечения нечетких множеств
- •4.6. Многокритериальный выбор альтернатив на основе нечеткого отношения предпочтения
- •4.7. Примеры прикладных задач
- •4.7.1. Выбор лучшего банка для размещения денежных средств физическим лицом
- •4.7.2. Выбор конкурентоспособного товара
- •4.8. Основные понятия лекции №4
- •Литература
- •Содержание
3.5.2. Условная максимизация с ограничениями по неравенству
Условие
![]() ,
является жестким. Во многих случаях
достаточно задавать ограничения сверху
(например, для затрат):
,
является жестким. Во многих случаях
достаточно задавать ограничения сверху
(например, для затрат):
![]() ,
,
или снизу (например,
для эффективности, надежности и т.п.):
![]() .
.
На рис. 8 приведено решение следующей задачи:
![]() .
.
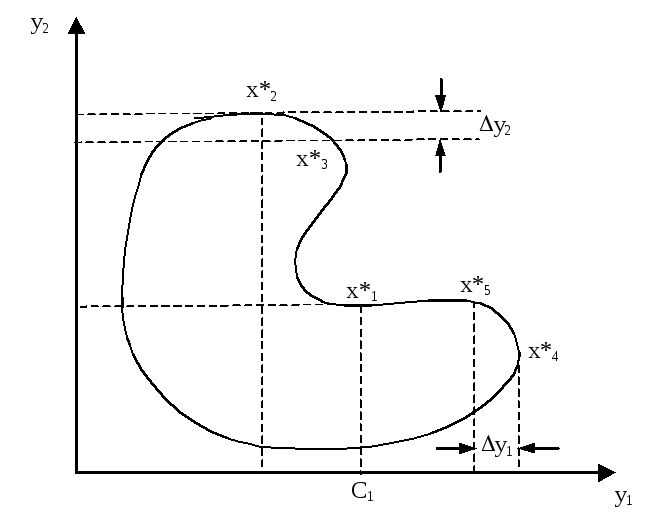
Рис.8. Условная максимизация
3.5.3. Метод уступок
Ограничения типа «равенство» и «неравенство» задают слишком сильное различие между основным и дополнительными критериями (рис. 8). Меньшее различие дает метод уступок. Он реализуется следующим алгоритмом:
Частные критерии упорядочиваются в порядке убывания их важности.
Находится наилучшая альтернатива по наиболее важному критерию (на рис. 8 это
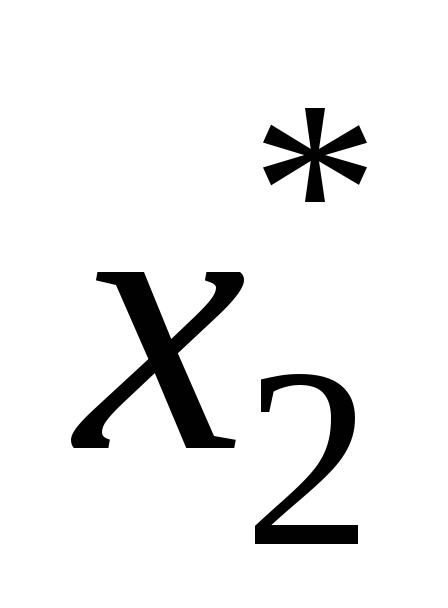 ,
если самый важный критерий
,
если самый важный критерий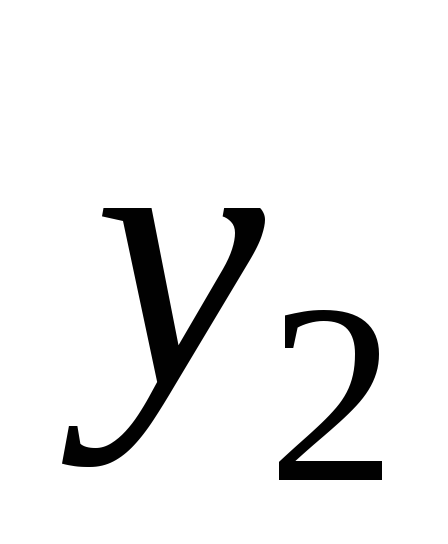 и
и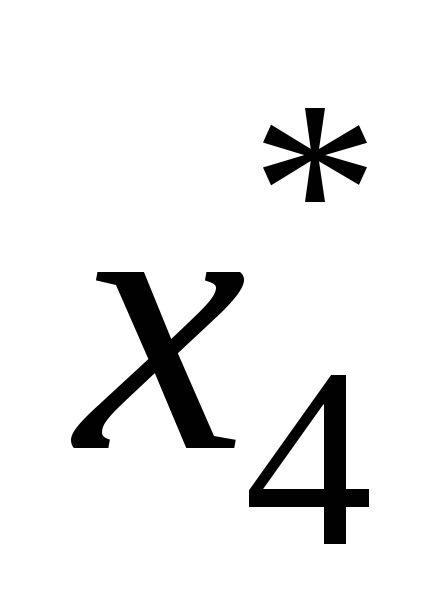 ,
если им является
,
если им является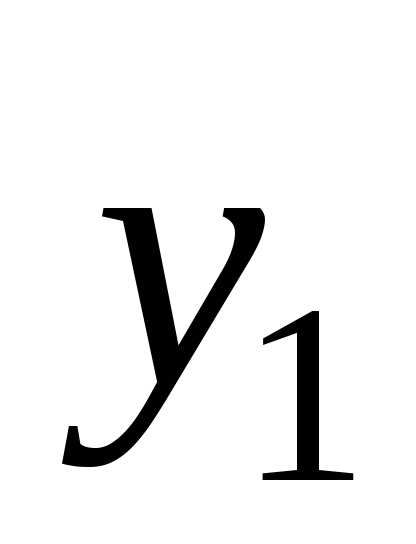 ).
).
Определяется
уступка
![]() –
величина, на которую возможно уменьшить
достигнутое значение самого важного
критерия, чтобы за счет нее увеличить,
насколько возможно, значение следующего
по важности критерия и т.д. (на рис. 8
полученные таким образом альтернативы
изображены точками
–
величина, на которую возможно уменьшить
достигнутое значение самого важного
критерия, чтобы за счет нее увеличить,
насколько возможно, значение следующего
по важности критерия и т.д. (на рис. 8
полученные таким образом альтернативы
изображены точками![]() и
и![]() ).
).
3.6. Сведение многокритериальной задачи к однокритериальной
Вычисляется
суперкритерий
![]() ,
представляющий собой скалярную функцию
векторного аргумента (свертку критериев):
,
представляющий собой скалярную функцию
векторного аргумента (свертку критериев):
![]() .
.
Суперкритерий
позволяет упорядочить альтернативы по
величине
![]() ,
выделяя наилучшую в смысле этого
критерия. Вид функции
,
выделяя наилучшую в смысле этого
критерия. Вид функции![]() определяется тем, как представляется
вклад каждого критерия
определяется тем, как представляется
вклад каждого критерия![]() в суперкритерий через весили. При этом
решаются две проблемы – уход от
размерности разномерных критериев и
выбор вида функциональной зависимости:
в суперкритерий через весили. При этом
решаются две проблемы – уход от
размерности разномерных критериев и
выбор вида функциональной зависимости:
Аддитивная функция (вектор весовых коэффициентов
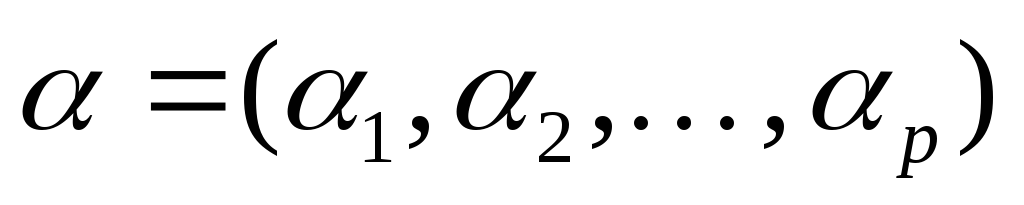 выражает вклад каждого критерия
выражает вклад каждого критерия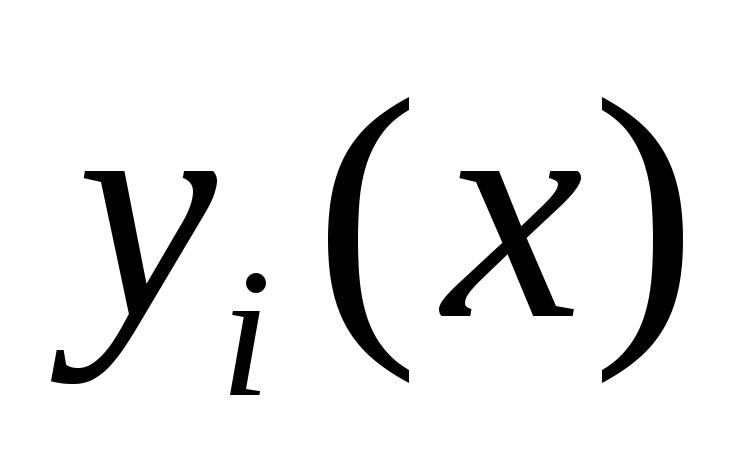 в суперкритерий):
в суперкритерий):
![]() ,
,
где si– нормирующий коэффициент, равный диапазону шкалы оцениванияi-го критерия;
Мультипликативнаяфункция (вектор весовых коэффициентов
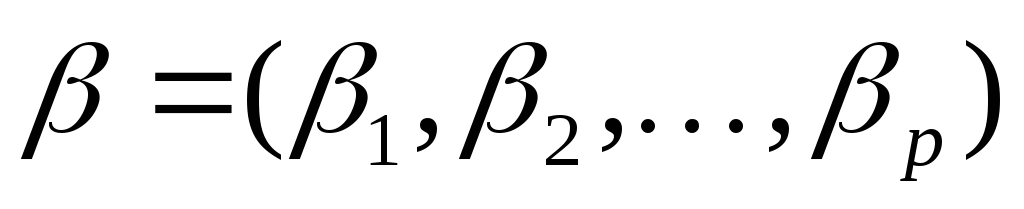 выражает вклад каждого критерия
выражает вклад каждого критерия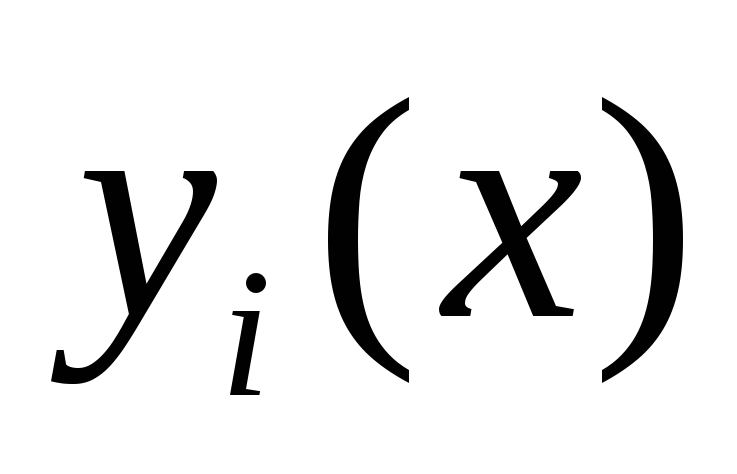 через вероятность достижения
соответствующего показателя качества):
через вероятность достижения
соответствующего показателя качества):
![]()
где
![]() .
.
Наилучшая альтернатива определяется формулой
![]() .
.
Недостаток метода заключается в том, что упорядочивание точек в p-мерном пространстве в принципене может быть однозначными полностью определяется видом упорядочивающей функции. Даже небольшое ее изменение варьированием коэффициентов может привести к большому различию новой и старой наилучших альтернатив, что характеризует неустойчивость процедуры выбора.
3.7. Способы нормализации локальных критериев
Проблема нормализации локальных критериев возникает во всех задачах векторной оптимизации, когда локальные критерии имеют различные единицы измерения (килограммы, метры, секунды, рубли и т.д.) Исключение составляет лишь метод относительной уступки в котором нормализация осуществляется автоматически. В основу нормализации положено понятие «идеального вектора» т. е. вектора с идеальными значениями локальных критериев
![]() .
.
В нормализованном пространстве критериев вместо действительного значения локального критерия yi рассматривается безразмерная величина
![]() .
.
В том
случае, если лучшим считается большее
значение критерия и если
![]() то
то![]() .
.
Успешное решение проблемы нормализации во многом определяется тем, насколько удачным окажется выбор параметров идеального вектора. Рассмотрим три основных способа задания идеального вектора.
1-й способ. Идеальный вектор определяется некоторыми заданными значениями локальных критериев. Эти заданные значения может определить, например, заказчик разработки. Формальная запись:
![]() .
.
Недостаток этого способа полнейший субъективизм выбора.
2-й способ. Идеальным считается вектор, параметрами которого являются максимально возможные значения локальных критериев
![]() .
.
3-й способ. В качестве параметров идеального вектора принимается максимально возможный разброс значений соответствующих локальных критериев, т.е.
![]() .
.
