4.2. Нечеткие модели оптимизации

Формализация качественной информации может выполняться на базе двузначной или нечеткой логики.

Когда используется двузначная логика, связь между переменными системы трактуется как «жесткая», т.е. возможны всего два варианта «0» ‑ связь отсутствует, «1» – связь имеется.

Более детальное описание характера связей между переменными достигается применением аппарата нечетких множеств, основанного на нечеткой логике, что позволяет формализовать более гибкие связи между параметрами и в большей степени соответствует природе изучаемых явлений и описанию взаимодействий на естественном языке.

Рассмотрим применение методологии нечетких множеств для построения моделей оптимизируемых систем.

4.2.1.Элементы теории нечетких множеств

В математике множество традиционно понимается как совокупность элементов (объектов), обладающих некоторым свойством. Для любого элемента при этом допускаются лишь две возможности: либо он принадлежит данному множеству (т.е. обладает данным свойством), либо нет. Таким образом в описании множества в обычном смысле должен содержаться четкий критерий, позволяющий судить о принадлежности (непринадлежности) любого элемента данному множеству.

Понятие нечеткого множества основано на представлении, что составляющие множество элементы, имеющие общее свойство, могут обладать им в различной степени и, следовательно, принадлежать данному множеству с различной степенью. При таком подходе высказывания типа «элемент xпринадлежит множеству» теряют смысл, поскольку необходимо указать «насколько сильно», т.е. с какой степенью выполняется это условие.

Приведем определения из теории нечетких множеств, которые потребуются в дальнейшем при формулировании и анализе задач нечеткой оптимизации.

Определение. Пусть X– конечное множество в обычном смысле. Нечеткое множествоАмножестваXхарактеризуется функцией принадлежности_А:X[0;1], которая ставит в соответствие каждомуxXдействительное число в интервале [0;1]. Число_А(x)называетсястепенью принадлежности x к нечеткому множеству А.

Чем ближе _А(x)к единице, тем выше степень принадлежностиxкА. Функция принадлежности является обобщением классической характеристической функции, принимающей лишь два значения: «1» (для элементов, принадлежащих множеству) либо «0» (для элементов, не принадлежащих ему).

Следует отметить, что в общем случае выбор функций принадлежности субъективен, и основан на качественной информации, имеющейся в каждом отдельном случае. Это всего лишь новая форма утверждения гипотез, отражающая субъективное представление эксперта (исследователя) об особенностях системы, о характере ограничений и целей исследования.

Пример. Для сравнения рассмотрим обычное множество чисели нечеткое множество чиселA={x«значениеxблизко к 1»} (рис. 11). Заметим, что вид функции принадлежности_Анечеткого множестваАзависит от того, что подразумевается под понятием «близко» в контексте анализируемой ситуации.

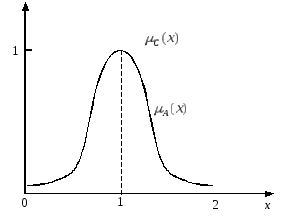
Рис. 11. Функции принадлежности

Обозначения к рис. 11:

–функция принадлежности обычному множеству ;

–функция принадлежности нечеткому множеству A={x«значениеxблизко к 1»}

Рассмотрим ряд определений теории нечетких множеств.

Носителем нечеткого множества Аназывается совокупность всех точекxXдля которых_A(x)>0.

Нечетное множество Анормальнотогда и только тогда, когда. В противном случае нечеткое множество называетсясубнормальным.

Непустое субнормальное нечеткое множество может быть нормализовано делением каждого _A(x)на величину.

Нечеткое множество пустотогда и только тогда, когда_A(x)=0 для всехxX.

Два нечетких множества равны(что записывается какA=B) тогда и только тогда, когдадля всехxX.

Нечеткое множество Асодержится в нечетком множествеВ, или является подмножествомВ(т.е.АВ), тогда и только тогда, когда.

ПересечениемАиВ(обозначаетсяАВ) называется наименьшее нечеткое множество, содержащееся как вА, так и вB, с функцией принадлежности

для всех xX

ОбъединениемАиВ(обозначаетсяАВ) называется наибольшее нечеткое множество, содержащее какАтак иВ, с функцией принадлежности

для всех xX

Приведем характерные свойства нечетких отношений, используемые при формализации и анализе математических моделей в реальных задачах принятия решений.

Известно, что отношением Rна универсальном множествеXназывается подмножество декартова произведенияXX. Задать отношение на множествеXозначает указать все пары элементовx,yX, такие, чтоxиyсвязаны отношениемR. Тот факт, что пара элементов (x,y)XXнаходится в отношенииR, записывают какxRyили (x,y)R.

Наиболее распространенной формой задания нечетких отношений является их словесное описание, например вида «Xпримерно равенY», «Aзначительно меньшеB» и т.п.

Определение. В тех случаях, когда связи между переменными (параметрами) исследуемой системы выражены нестрого, целесообразно формализовать отношения в соответствии со следующим определением: нечетким отношением R на множестве Xназывается нечеткое подмножество декартова произведенияXX, характеризующееся функцией принадлежности

.

Функция принадлежности _R(x,y)понимается как субъективная мера (степень) выполнения отношенияxRy.

Если множество X– дискретно и конечно, т.е., то функция принадлежности_Rможет быть задана матрицейRразмера (nn), элементами которой могут быть числа из интервала [0;1].

Если элемент матрицы r_ijравен, то степень выполнения отношенияравна.

Пример. Пусть элементы множествазадают время завершения изучаемой химической реакции при различных режимах ее реализации.

Матрица Rотношения «x_iприблизительно равенx_j», заданная исследователем может иметь, например, такой вид:

Элемент r₂₄=0.1означает, что степень выполнения отношения «времяx₂=14 приблизительно равно времениx₄=18» равна 0.1, т.е., хотя и незначительно, но все же отлична от нуля.

В прикладных задачах особое значение имеет произведение или композиция нечетких отношений.

Определение. Максиминное произведение нечетких отношенийR₁иR₂на множествеXзадается функцией принадлежности вида

.

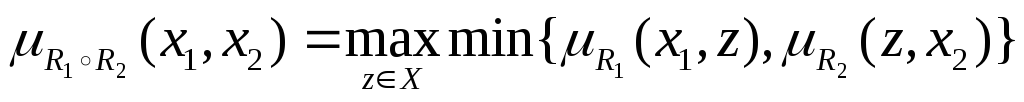В конечном множестве Xматрица нечеткого отношения равна максиминному произведению матриц нечетких отношенийR₁иR₂(в данном случае оно представляет собой операцию, аналогичную умножению матриц, но при этом вместо арифметических операций умножения и сложения используются операции нахождения минимального и максимального элементов соответственно).

Пример.

Определение. Минимаксное произведениенечетких отношенийR₁иR₂на множествеXопределяется следующей функцией принадлежности

.

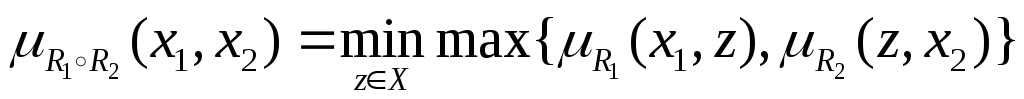Пример.