3.8. Способы задания и учета приоритета локальных критериев

Обычно используются три способа задания: с помощью ряда приоритета, вектора приоритета и весового вектора.

1. Ряд приоритета указывает на то, что локальные критерии, записанные в скобках левее, более важны, чем локальные критерии, записанные правее, т. е. самым важным является критерийy₁ вторым по важности является критерий y₂ затем y₃ и т.д.

В том случае, если имеются равноприоритетные критерии, они выделяются скобками т.е. критерии 3, 4, 5 ‑ равноприоритетны и занимают третье место по важности. Это чисто качественный способ задания приоритетов. При таком способе обычно используется принцип«жесткого приоритета», т. е. не допускается ни малейшего снижения критерия, стоящего левее в ряду приоритета.

2. Вектор приоритета ‑ это способ количественного задания приоритетов. Компоненты этого вектора _i определяют степень относительного превосходства двух соседних критериев из ряда приоритета, т.е. _i определяет, во сколько раз критерий y_i важнее критерия y_i+1 в том случае, если y_i и y_i+1, равны по важности, то и . Для удобствавсегда.

3. Весовой вектор представляет собой pмерный вектор, компоненты которого связаны соотношениями:

.

Компонента _i показывает степень относительного превосходства критерия y_i над всеми оставшимися критериями. Обычно если необходимо количественно задавать приоритет критериев, то его задают в виде ряда приоритета, поскольку там сравнение идет только между двумя соседними критериями; затем с помощью соотношения:

(12)

переходят к весовому вектору. И тогда выбор наилучшего варианта производится с помощью всего вышеописанного аппарата, только вместо компонент вектора используются компоненты. Такой подход называют принципом гибкого приоритета.

Для случая 3-х локальных критериев соотношения (12) переписываются в виде

,

где .

3.9. Пример многокритериальной задачи принятия решений

Для отдела центрального конструкторского бюро (ЦКБ) необходимо устройство для вывода на печать конструкторских чертежей (плоттер). Имеются плоттеры трех моделей. Каждая модель характеризуется тремя локальными критериями:

• максимально возможный формат отпечатанного чертежа F (мм);

• разрешение чертежа R (dpi);

• объем буфера V (КБайт).

Конкретные значение указанных локальных критериев для каждого из вариантов представлены в таб.3.

Таблица 3

Критерии № вар.	F	R	V
1	4	20	64
2	8	14	128
3	10	12	256

Требуется, используя известные схемы компромисса, определить лучший вариант плоттера:

а) без учета приоритета локальных критериев;

б) с учетом приоритета локальных критериев.

1. Нормализация исходных данных.

Поскольку локальные критерии имеют различную размерность прежде всего необходимо нормализовать исходную таблицу 3. Для этого используем соотношение

.

В качестве параметров идеального вектора выбираем максимально возможные значения параметров:

.

Переходим от табл.3 к табл.4, в которой записаны нормализованные значения локальных критериев.

Таблица 4

Критерии № вар.	F	R	V
1	0.4	1	0.25
2	0.8	0.7	0.5
3	1	0.6	1

2. Выбор наилучшего варианта без учета приоритета локальных критериев. Воспользуемся известными схемами компромисса.

2.1. Принцип справедливой уступки. Известны две модификации этого принципа.

Принцип абсолютной уступки. Формально он записывается следующим образом:

.

В этом выражении J⁽⁺⁾ ‑ подмножество мажорируемых, т.е. увеличиваемых, критериев; I^(-) ‑ подмножество минорируемых, т.е. уменьшаемых, критериев; ‑ абсолютное значение величин приращения. Причем, как следует из определения,.

Лучшим, по принципу абсолютной уступки, считается компромисс, при котором значение суммы снижения одного или нескольких критериев не превышает абсолютного значения суммы приращений оставшихся критериев.

Можно показать, что этому принципу соответствует модель максимизации суммы локальных критериев:

т.е. ищется сумма по строкам всех локальных критериев:

и та из этих сумм, которая окажется максимальной, соответствует лучшему варианту.

Воспользуемся этими соотношениями:

1-й вариант: ;

2-й вариант: ;

3-й вариант: .

Просматривая значения полученных сумм, выбираем максимальное значение, это и будет наилучшим вариантом.

Вывод: если задаться принципом абсолютной уступки, то предпочтение следует отдать варианту № 3.

Принцип относительной уступки. Формально он записывается с помощью следующего соотношения:

,

где есть относительные значения приращения локальных критериев.

В каждом столбце находится максимальное значение локального критерия. После этого необходимо перейти к новой таблице, поделив все числа в столбцах предыдущей таблицы на максимальное значение в каждом столбце. Далее, с этой новой таблицей выполняются те же процедуры, что и в принципе абсолютной уступки. Можно показать, что при использовании этого компромисса оптимальному варианту соответствует модель максимизации произведения локальных критериев. Формально:

Или, для случая трех критериев: для каждой строчки вычисляется произведение:

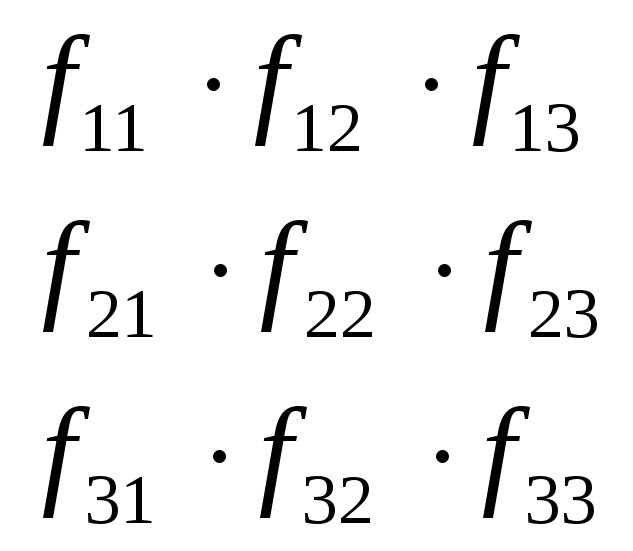
и среди этих произведений ищется максимум  это и будет лучший вариант по данному компромиссу.

Используя эти соотношения, получим:

1-й вариант: ;

2-й вариант: ;

3-й вариант: .

Вывод: если в качестве схемы компромисса выбрать принцип относительной уступки, то предпочтение следует отдать варианту № 3.

2.2. Принцип последовательной уступки.

Пусть важность локальных критериев соответствует их последовательной записи в табл. 3, т. е. самым важным параметром является формат, менее важным  разрешение, и наименее важным  объём памяти. Просматриваем первый столбец табл. 4 и выбираем вариант, в котором F достигает максимума:

max{0.4; 0.8; 1}=1.

Пусть теперь мы согласны наложить «уступку» на критерий F, и пусть эта «уступка» будет равна f₁=0.5; тогда имеем

таким образом, мы допускаем к рассмотрению все варианты, в которых F не хуже, чем 0.5. От табл. 4 переходим к табл. 5, где отображено это условие.

Таблица 5

Критерии № вар.	F	R	V
1			
2	0.8	0.7	0.5
3	1	0.6	1

Из рассмотрения исключается первый вариант. Теперь в табл.5 выбираем наилучший вариант по критерию R  это 0.7. Таким образом, при наложении уступки на критерий F, равный 0.5, мы пришли к выбору варианта два.

Совершенно аналогично можно наложить уступку и на второй по важности критерий. Мы не будем этого делать.

Вывод: при использовании принципа последовательной уступки выбирается второй вариант.

3. Выбор наилучшего варианта с учетом приоритета локальных критериев.

Пусть приоритет критериев задан следующим вектором . Переходим к весовому вектору:

;

; ;.

Имеем:

.

И от табл. 4 переходим к табл. 6, в которую подставляем вместо .

Таблица 6

Критерии № вар.	F	R	V
1	0.16	0.4	0.05
2	0.32	0.28	0.1
3	0.4	0.24	0.2

Теперь воспользуемся известными схемами компромисса

3.1 Принцип справедливой уступки

Принцип абсолютной уступки. Воспользуемся здесь и ниже материалом, изложенным в первой части задачи:

1-й вариант  ;

2-й вариант  ;

3-й вариант  (max).

Просматривая значения полученных сумм, выбираем максимальное значение, это и будет наилучшим вариантом.

Вывод: если задаться принципом абсолютной уступки, то предпочтение следует отдать варианту №3.

Принцип относительной уступки:

1-й вариант  ;

2-й вариант  ;

3-й вариант  (max).

Просматривая полученные значения, выбираем максимальное значение, это и будет наилучшим вариантом.

Вывод: если в качестве принципа выбрать принцип относительной уступки, то предпочтение следует отдать варианту №3.

3.2. Принцип последовательной уступки.

Пусть важность локальных критериев соответствует их после­довательной записи в табл. 6, т.е. важнейшим параметром является формат, менее важным  разрешение, и наименее важным  объём памяти. Просматриваем первый столбец табл. 6 и выбираем вариант, в котором F достигает максимума:

max{0.16; 0.32; 0,4}=0.4.

Пусть теперь мы согласны наложить «уступку» на критерий F, и эта «уступка» будет равна f₁= 0.15, тогда имеем

,

таким образом, мы допускаем к рассмотрению все варианты, в которых F не хуже, чем 0.25. От табл. 6 переходим к табл. 7, где отображено это условие:

Таблица 7

Критерии № вар.	F	R	V
1			
2	0.32	0.28	0.1
3	0.4	0.24	0.2

Из рассмотрения исключается первый вариант. Теперь в табл. 7 выбираем наилучший вариант по критерию R, это 0.28. Таким образом, при наложении уступки на критерий F, равной 0.15, мы пришли к выбору второго варианта.

Вывод: при использовании принципа последовательной уступки выбирается второй вариант.