scherbo-sp2

2. Краткие теоретические сведения

Балки, для определения внутренних усилий которых недостаточно одних только уравнений равновесия, называются статически неопреде-

лимыми.

Для расчета таких балок, кроме уравнения статики, необходимо со- ставлять дополнительные уравнения.

Рассмотрим балку, соответствующую расчетной схеме лабораторной установки.

Число неизвестных опорных реакций равно четырем: три реакции заделки и одна реакция подвижной опоры. Уравнений статики три, таким образом, система один раз статически неопределима. От расчета статиче- ски неопределимой балки перейдем к расчету статически определимой, образованной удалением лишних связей. Для того чтобы полученная таким образом статически определимая система была статически эквивалентна заданной, необходимо действие удаленных связей заменить реакциями связей.

Полученную статически определимую систему будем называть ос- новной системой. Чтобы основная система была кинетически эквивалент- ной заданной, необходимо приравнять нулю перемещение в основной сис- теме от действия нагрузки и реакций по направлению последних.

Применительно к данной балке один из вариантов основной системы может быть получен удалением опорной связи В и заменой реакцией связи.

Для данной балки кинематическая эквивалентность заданной и ос- новной систем будет выражаться уравнением

1 = 1р ÷ х1,

где D1 – перемещение по направлению удаленной связи в основной сис- теме по направлению реакций К1;

D1р, Dх1 – соответственно перемещения в основной системе от на- грузки Р и от реакции связи Х1 по направлению реакции Х1.

Для линейно деформированной системы перемещение от реакции Х1 по своему направлению будет равно перемещению от действия единичной силы по направлению Х1, умноженному на величину реакции связи, т. е.

Dx1 = d11 × Х1,

где d11 – перемещение в основной системе от действия единичной силы по направлению реакции Х1.

Тогда d11 × X1 + D1P = 0.

Для определения единичного перемещения d11 необходимо построить единичнуюопору m1 и перемножить саму на себя по правилу Верещагина:

321

Для определения перемещения от нагрузки в основной системе не- обходимо построить эпюру Мр от действия нагрузки в основной системе и умножить ее по правилу Верещагина на эпюру m1:

Решение этой задачи возможно и другими способами с помощью урав- нения трех моментов, с использованием универсального уравнения трех мо- ментов, с использованием универсального уравнения упругой линии.

3. Постановка и порядок проведения работы

На опыте осуществлена основная статически определимая система в виде стального стержня, жестко закрепленного одним концом к станине. Нагрузка передается балке при помощи серьги с крюком, на который под- вешивается груз.

Вертикальная сила В = Х1, заменяющая реакцию отброшенной связи (опоры), получается от натяжения нити, переброшенной через блок, и пе- редается балке через серьгу.

Устанавливаем серьгу в точке С. В точке В устанавливаем прогибо- мер так, чтобы на шкале индикатора малая стрелка была около единицы. Затем подвешиваем на крючок серьги С груз, под влиянием которого балка прогибается вниз. Прогибомер даст новое показание. Отмечать отсчет это- го показания не надо, нужно лишь добиться такого увеличения давления со стороны серьги на балку, чтобы прогиб был равен нулю, т. е. чтобы пока- зания прогибомера вернулось бы к первоначальному. Для достижения этой цели производим подбор грузов на крюке.

Лабораторная работа проводится в следующем порядке:

1.Произвести замер размеров поперечного сечения балки b и h, а также размеров D и l и занести в табл. 1.

2.Дать предварительное натяжение индикатору, равное 1 при отсче- те по малой шкале.

3.Нагрузить балку нагрузкой Р.

4.Постепенно увеличивая груз В, добиться прежних показаний ин- дикатора.

5.Занести значение В в табл. 1.

6.Определить по формуле (1) теоретическое значение опорной реакции.

322

Обработка результатов наблюдений

1.Определить статически величину опорной реакции.

2.Определить процентное отношение величин опорной реакции, оп- ределенной статически и экспериментально.

Полученные результаты оформить в соответствии с формой журнала лабораторной работы № 12.

5. Анализ полученных результатов

На основании результатов опытов установить линейный характер за- висимости величины реакции В от нагрузки Р, выявить точность опреде- ления расчетов величины опорной реакции в статически неопределимой балке без учета сдвиговых деформаций.

6. Выводы

Сделать вывод о характере зависимости величины реакции В от на- грузки Р, от точности проведенного эксперимента.

7.Контрольные вопросы

1.Какими способами можно теоретически определить величину ре- акции для данной статически неопределимой балки? (Уметь использовать для определения реакции способы, известные из прохождения курса «Со- противление материалов»).

2.Чем объясняются некоторые расхождения теоретических и опыт- ных данных?

3.В каких случаях для определения перемещений можно применить способ Верещагина?

4.Какие еще основные системы могут быть выбраны для данной

балки?

5.Какие системы называются статически неопределимыми?

ЛАБОРАТОРНАЯ РАБОТА № 12

Исследование деформации консольной балки при косом изгибе

1. Цель работы

Экспериментальное определение прогиба свободного конца кон- сольной балки при косом изгибе с последующим сравнением опытных данных с результатами теоретического расчета.

2. Краткие теоретические сведения

Деформация, при которой силы, действуя перпендикулярно оси бал- ки, не лежат в главной центральной плоскости, называется косым изгибом.

323

Возможны два случая косого изгиба: плоский и пространственный. В первом из них все внешние силы лежат в одной плоскости, во втором – расположение сил произвольно.

В данной работе рассматривается случай плоского косого изгиба

(рис. 1).

Рис. 1

Балка нагружена силой Р, действующей под углом α к одной из главных центральных осей поперечного сечения (к оси Y). Разложим силу на две составляющие – Рх вдоль оси X и Рy вдоль оси Y.

Px = P sin α, Py = P cos α.

Каждая из составляющих вызывает прямой поперечный изгиб. Сле- довательно, косой изгиб можно рассматривать как сумму двух прямых из- гибов, происходящих в главных центральных плоскостях. Изгиб в плоско- сти ZOY вызывает сила Ру. Напряжение в любой точке произвольного по- перечного сечения вычисляем по формуле

sM x = M x × y,

J x

где Мх – изгибающий момент в рассматриваемом поперечном сечении относительно главной центральной оси Х;

Jx и y – соответственно осевой момент инерции и координата иссле- дуемой точки относительно той же оси Х.

Отметим, что нормальное напряжение на площадке, совпадающей с плоскостью поперечного сечения, будет параллельно продольной оси бру- са (оси Z).

324

Теперь независимо от этого расчета рассмотрим изгиб силы Рх. Учи- тывая предыдущие рассуждения, найдем

σ = σM x + σM y

Знак как первого, так и второго членов устанавливаем в зависимости от растяжения (+) или сжатия (-) в исследуемой точке. Например, для точ- ки К (рис. 1) первый член нужно записать со знаком плюс, второй – со зна- ком минус, так как при изгибе в вертикальной плоскости в этой точке про- исходит растяжение, а при изгибе в горизонтальной – сжатие. Если необ- ходимо в поперечном сечении построить эпюру напряжений σ, то предва- рительно находим положение нейтральной линии. Она пройдет через центр тяжести сечения и те квадраты, которые не пересекает сила Р. Угол β между нейтральной осью и осью Х отсчитываем в том же направлении, что и угол α. Величину угла β найдем из выражения

tgb = J x × tga.

J y

Перпендикулярно нейтральной оси вне сечения проведем прямую (рис. 2). От нее параллельно нейтральной оси отложим отрезки, которые в оп- ределенном масштабе показывают напряжения в точках, лежащих на этой ли- нии. Из формулы нормальных напряжений видно, что эпюра будет линейной.

Для определения перемещения конца консоли (см. рис. 1) рассмот- рим изгиб в вертикальной плоскости (плоскость ZOY). Перемещение конца консоли в этой плоскости можно найти с помощью уравнения изогнутой оси или графоаналитическим способом Верещагина (рис. 3, а, б, в, г).

325

Воспользуемся вторым методом. Строим эпюру изгибающих момен- тов от нагрузки Ру (рис. 3, б). В направлении искомого прогиба fy прило- жим единичную силу и построим эпюру М – изгибающих моментов от единичной силы (рис. 3, г). В том и другом случае реакции в заделке не вычисляем, так как построение эпюр изгибающих моментов ведем со сто- роны свободного конца. По способу Верещагина площадь эпюры Мр нуж-

но умножить на ординату M из второй эпюры, расположенную под цен- тром тяжести первой эпюры, и полученный результат разделить на жест- кость при изгибе EJx, которая соответствует изгибу бруса в плоскости ZOY. Получим составляющую прогиба по направлению оси Y

Составляющую прогиба fx находим таким же способом, рассмотрев изгиб в горизонтальной плоскости. По аналогии можно записать

fx = Pa2 (3l − a)sin α .

6EJ y

Так как прогибы fx и fy перпендикулярны друг другу, то полный про- гиб f равен

f = fx2 + f y2 .

Прогиб f по направлению не совпадает с линией действия силы Р, как это было при прямом изгибе. Отсюда и произошло название – косой изгиб. При плоском косом изгибе направление прогиба перпендикулярно нейтральной линии.

3. Постановка и порядок проведения работы

Лабораторная работа выполняется в следующей последовательности: 1. Согласно исходным данным (плечо нагрузки, угол поворота об-

разца и т. д.), указанным преподавателем, составить расчетную схему.

2.Подготовить установку (рис. 4) для выполнения опыта.

3.Установить стрелки индикатора на «0».

4. Определить величину ступени нагрузки – Р.

326

Затем, давая одинаковые приращения нагрузки, произвести 3-4 на- гружения исследуемого образца в упругой зоне. Наибольшая нагрузка не должна превышать величину, указанную в технической характеристике.

5. После каждого нагружения регистрировать по шкалам индикато- ров величины приращений составляющих полного прогиба свободного

Убедиться в линейной зависимости перемещений от нагрузки.

6. По окончании опыта образец разгрузить и сравнить показания ин- дикаторов после разгрузки с первоначальными.

Грузы в нерабочем положении

Рис. 4. Общий вид установки

327

4. Обработка результатов измерений

Вычислить средние арифметические значения величин приращения составляющих полного прогиба в процессе опыта по формулам:

Приращение полного прогиба

Dfопыт = Dwср2 + Dvср2 .

5. Анализ полученных результатов

Произвести теоретический расчет величин прогиба свободного кон- ца в вертикальном и горизонтальном направлениях.

При определении прогиба исходим из принципа независимости дей- ствия сил и вычисляем составляющие полного прогиба в каждой из глав- ных плоскостей.

Консольная балка нагружена на свободном конце силой Р. Раскла- дывая Р по направлениям главных осей, получим составляющие

Py = P cos α; Px = P sin α.... ,

где α – угол поворота образца.

Величины прогибов в главных плоскостях могут быть определены по правилу Верещагина.

Полный прогиб

Df = Dw2 + Dv2 .

Расхождение между опытными данными и теоретическими вычисле- ниями:

Сформулировать выводы на основании анализа экспериментальных

итеоретических данных.

7.Контрольные вопросы

1.Дайте определение косого изгиба.

2.Чем плоский косой изгиб отличается от пространственного?

3.По какой формуле определяются нормальные напряжения при ко- сом изгибе?

328

4.Какое напряженное состояние имеет место в каждой точке балки при косом изгибе?

5.Как можно найти напряжение опытным путем?

6.Как провести испытание по определению перемещений и напря-

жений?

7.Как экспериментально найти прогиб торцового сечения балки?

8.Объясните устройство стрелочного индикатора.

9.Как направлен прогиб по отношению к действующей силе?

10.Как можно теоретически определить перемещение сечения при косом изгибе?

11.Как сопоставить составляющие прогиба, полученные из опыта и на основании теоретического расчета?

ЛАБОРАТОРНАЯ РАБОТА № 13

Опытная проверка теории внецентренного растяжения

1.Цель работы

1.Изучить методику испытаний на внецентренное растяжение.

2.Определить опытным путем величины нормальных напряжений в характерных точках поперечного сечения бруса при внецентренном растя- жении и сравнить величины напряжений, полученных опытным путем, с вычисленными теоретически.

2.Краткие теоретические сведения

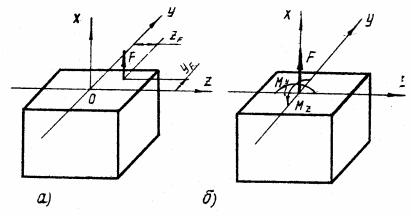
Если линия действия сил, растягивающих брус, не совпадает с гео- метрической осью бруса (рис. 1, а), то такой брус подвергается внецен- тренному растяжению. При приведении растягивающей силы к центру тя- жести поперечного сечения (рис. 1, б) видим, что брус подвергается не только растяжению, но и изгибу.

Рис. 1

329

Величина продольной силы N = F, а величины изгибающих момен- тов Mz и Му равны

М z = F × yF ;

M y = F × zF ,

где F – величина растягивающей нагрузки,

yF, zF – координаты приложения растягивающей нагрузки. Напряжения в любой точке поперечного сечения бруса будут скла-

дываться из нормальных напряжений от продольной силы и сгибающих моментов

ной центральной оси у.

Уравнение нейтральной оси легко можно получить из выражения (3), приравняв нормальные напряжения s к нулю

Применительно к данной лабораторной работе расчетная схема на внецентренное растяжение будет иметь вид, изображенный на рис. 2.

330