
scherbo-sp2
.pdf
следовательно,
y » |
J x |
|
|
0 |
. |
(13.11) |
|
|
|||
0 |
RF |
|
|
|
|
||
Так, например, для прямоугольного сечения получим
|
bh3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
h2 |
|
|
12 |
|
|
|
||||
y » |
|
|
|
= |
|
|||
|
|
|
|
|
|
; |
||
|
|
|
|
|
||||
0 |
|
Rbh |
|
|
12R |
|||
|
|
|
|
|||||
для круглого сечения
y0 » d 2 . 16R
Приближенные формулы (табл. 13.1) дают хорошую точность для брусьев средней кривизны, когда h < 1 .
R2
13.5.Напряжение при одновременном действии продольной силы и изгибающего момента
Если в сечении кривого бруса одновременно возникают изгибающий момент и продольная сила, то напряжение следует определять как сумму напряжений от двух указанных воздействий:
s = N ± M × y . |
(13.12) |
FSx r
Вэтой формуле величина изгибающего момента должна быть найдена
относительно оси, проходящей через центр тяжести сечения, так как на- пряжение от продольной силы N/F найдено из условия, что нормальная сила приложена в центре тяжести поперечного сечения.
Пример
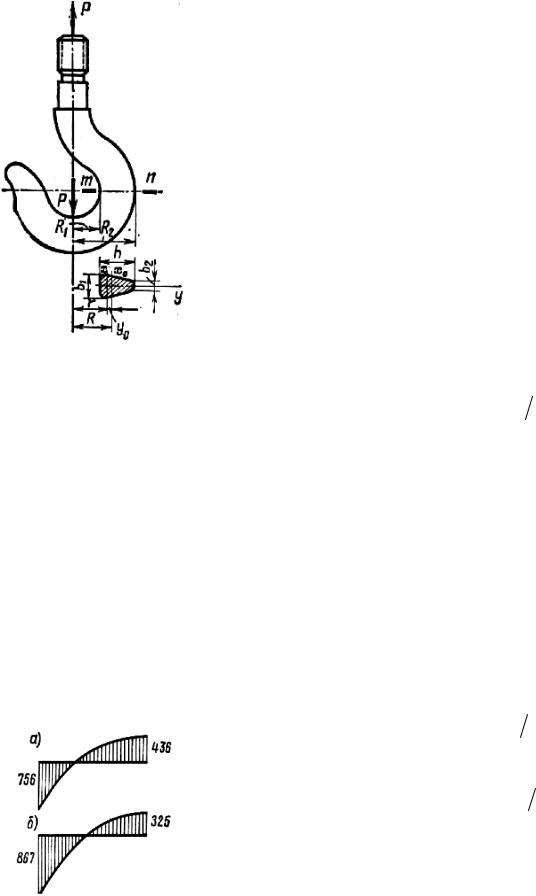
Рассмотрим пример расчета крюка, изображенного на рис. 13.10, где Р = 2,5 тс. Поперечное сечение крюка можно рассматривать как трапецию с размерами: b1 = 4 см, b2 = 1 см, h = 9 см, R1 = 3 см, R2 = 12 см, расстояние от центра кривизны до центра тяжести
R = R + |
b1 + 2b2 |
× |
h |
= 3 + |
4 + 2 ×1 |
|
= 6,6 см. |
|||||||
|
|
|
||||||||||||
|
|
1 |
b1 + b2 |
3 |
|
|
|
4 +1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
Радиус кривизны нейтрального слоя (табл. 13.1) |
||||||||||||||
r = |
|
|
(4 +1)92 |
|
|
|
|
= 5,72 см. |
||||||
|
|
|
|
|
|
12 |
|
|
|
|
||||
2 |
(4 |
×12 -1×3)ln |
|
|
- 9(4 -1) |
|
||||||||
3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Величина смешения нейтрального слоя относительно центра тяжести y0 = R − r = 6,6 − 5,72 = 0,88 см.
141
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Площадь сечения |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F = |
b1 + b2 |
h = |
4 +1 |
9 = 22,5 см2 ; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
статический момент сечения относительно |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
нейтральной оси |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
x |
= Fy = 22,5 ×0,88 =19,8 см3. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Координаты крайних точек сечения: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn = R2 − r = 12,00 − 5,72 = 6, 28 см; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ym = R1 - r = 3,00 - 5,72 = -2,72 см; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρn = R2 = 12 см; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rm = R1 = 3 см. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Нормальная сила и изгибающий момент в сечении |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N = 2500кгс; |
M = PR =16500кгс×см. |
|||||||||||||||
Рис. 13.10 |
|
|
|
|
|
|
|
|
По формуле (13.12) находим напряжения в |
|||||||||||||||||||||||
|
|
|
|
|
крайних волокнах: |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
sm |
= |
N |
+ |
M |
× |
ym |
= |
2500 |
+ |
16500 |
× |
2,72 |
=111 + 756 = 867 кгс см2 ; |
|||||||||||||||||||
|
|
|
rm |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
F Sx |
|
|
22,5 |
|
|
19,8 |
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||
|
sn = |
N |
+ |
M |
× |
yn |
= |
2500 |
- |
16500 |
× |
6, 28 |
=111 - 436 = -325. |
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
F |
|
Sx |
|
rn 22,5 |
|
|
19,8 |
12 |
|
|
|
|
|
|||||||||||||||
Эпюра напряжений от одного только изгибающего момента показана на рис. 13.11 а, а от совместного действия нормальной силы и изгибающего момента – на рис. 13.11, б.
Интересно сравнить полученные результаты с теми, которые будут определены по обычным формулам для прямого бруса. Момент инерции се-
чения относительно центра тяжести равен |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
b h3 |
|
(b - b )h3 |
|
|
b + b |
|
b + 2b |
|
h |
2 |
4 |
|
||||||||||||
J x |
= |
2 |
+ |
1 2 |
- |
|
1 2 |
|
h |
1 |
2 |
× |
|
|
=134 см |
|
. |
||||||||
3 |
12 |
2 |
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||
0 |
|
|
|
|
|
|
|
b1 + b2 |
|
|
|
||||||||||||||
Далее находим напряжения от изгиба: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
sm |
= |
M |
ym = |
16500 |
3,6 = 443 кгс см2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
J x |
|
|
134 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
(вместо 756 кгс/см2); |
|
|
|||||||||||||
|
|
|
|
sn = |
M |
yn |
= - |
16500 |
5, 4 = -665 кгс см2 |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
J x |
|
|
134 |
|
|
|
|
кгс/см2). |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
(вместо – 436 |
|
|
|||||||||||||
|
|
|
|
Эти цифры убедительно показывают, что для |
|||||||||||||||||||||
|
|
|
|
расчета |
кривых брусьев, вообще говоря, нельзя |
||||||||||||||||||||
Рис. 13.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
142

пользоваться формулами, полученными для прямого бруса. Погрешность может быть настолько значительной, что не только количественные вели- чины напряжений, но и качественная картина напряженного состояния рез- ко изменяются. Так, например, при правильном расчете на изгиб наиболее напряженной точкой оказалась точка m, лежащая на внутренней кромке се- чения, в то время как при расчете по формулам прямого бруса, наоборот, напряжения в точке n от изгиба оказались больше, чем в точке m. Поэтому
кривые брусья разделяют на две группы: брусья малой кривизны h < 1 и
R 5
брусья большой кривизны h > 1 .
R 5
Для определения напряжений в брусьях малой кривизны приближен- но можно пользоваться формулами прямого бруса.
Для выяснения влияния кривизны на погрешность в напряжениях в кривом брусе, подсчитываемых по формулам для прямого бруса, составле- на табл. 13.2. В ней приводится процент расхождения между двумя указан- ными напряжениями для бруса с прямоугольным сечением.
Таблица 13.2
|
Брусья большой кривизны |
Брусья малой кривизны |
||||
|
|
|
|
|
|
|
R/h … |
2 |
3 |
5 |
8 |
10 |
∞ |
Δσ, % … |
18,2 |
11,8 |
6,9 |
4,8 |
3,4 |
0 |
|
|
|
|
|
|
|
Из этой таблицы видно, что при R/h > 5 напряжения допустимо опре- делять по формуле для прямого бруса.
143
М-14. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
14.0. Введение в модуль
Модуль содержит следующие структурные элементы:
1.Основные понятия.
2.Метод Эйлера для определения критических сил. Вывод формулы
Эйлера.
3.Влияние способов закрепления концов стержня на величину крити- ческой силы.
4.Пределы применимости формулы Эйлера. Формула Ясинского.
5.Выпучивание упруго-пластического центрально-сжатого стержня в условиях возрастающей нагрузки (понятие о теории Ф.Р. Шенли).
6.Расчет внецентренно-сжатой гибкой стойки.
7.Практический расчет сжатых стержней.
Цель модуля – изучить методику расчета прочности с учетом устой- чивости.
14.1.Основные понятия
Впредыдущих главах рассматривались методы определения напря- жений и деформаций при растяжении, сжатии, кручении и изгибе. Были также установлены критерии прочности материала при сложном сопротив- лении.
Однако во многих случаях проектирования инженерных сооружений обычных расчетов на прочность бывает недостаточно для того, чтобы полу- чить полное представление о работе сооружения.
Выяснение того, что напряжения не превосходят расчетного сопро- тивления материала, не дает еще права сделать вывод о безопасности суще- ствования сооружения.
Наряду с проблемой прочности существует проблема так называемой устойчивости сооружения или его элементов.
Инженерные объекты помимо нагрузок, учитываемых расчетом, все- гда подвергаются дополнительным малым воздействиям (возмущениям), стремящимся вывести данное тело из его расчетного состояния равновесия или движения.
Если малые возмущения вызовут малые отклонения системы от рас- четного (невозмущенного) состояния, то это состояние системы является устойчивым. Наоборот, если при малых возмущениях возникнут большие отклонения системы от расчетного состояния, то последнее является не- устойчивым.
Наглядным примером устойчивого или неустойчивого состояния мо-
жет служить вращение обычного волчка (гироскоп). Хорошо известно, что
144
чем больше скорость вращения волчка, тем большее сопротивление он ока- зывает попыткам отклонить его от вращения вокруг вертикальной оси. Таким образом, вращательное движение волчка при больших скоростях по отноше- нию к малым возмущениям устойчиво. При уменьшении скорости вращения ниже некоторого значения те же малые возмущения резко изменят его со- стояние и вызовут беспорядочные движения. Таким образом, при малых ско- ростях вращения движение волчка становится неустойчивым.
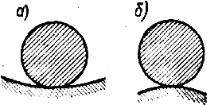
Примером устойчивого или неустойчивого равновесия является рав- новесие тяжелого шарика, лежащего в вогнутой или на выпуклой сфере (рис. 14.1). В первом случае (рис. 14.1, а) при любом малом склонении ша- рик стремится вернуться в исходное состояние. Исходное и отклоненное со- стояния шарика мало отличаются друг от друга. Во втором случае (рис. 14.1, б) при любом малом отклонении шарик покатится вниз. Возму- щенное и заданное состояния шарика резко отличаются друг от друга.
Шарик, лежащий на дне вогнутой сферы, находится в устойчивом равновесии, а на вершине выпуклой сферы его равновесие неустойчиво.
Аналогичные явления можно наблюдать при изучении равновесия сжатого стержня. При малой сжимающей силе, меньшей некото- рого критического значения Р < Ркр, сжатый стержень нечувствителен к малым возмуще-
ниям. Незначительные дополнительные воздействия мало отклоняют стер- жень от его прямолинейного состояния. При Р > Ркр прямолинейная форма сжатого стержня неустойчива. Сколь угодно малые случайные воздействия вызовут большие отклонения. Стержень после устранения возмущений ос- танется в изогнутом состоянии под действием продольной силы. Такое со-
стояние называют продольным изгибом.
Появление продольного изгиба опасно тем, что при нем происходит очень сильное нарастание прогибов при малом нарастании сжимающей си- лы. Прогибы и нагрузка связаны между собой нелинейной зависимостью. Быстрое нарастание прогибов вызывает быстрое нарастание напряжений от изгиба, которые в свою очередь приводят к ускорению деформаций и часто к разрушению стержня.
Для тонких (гибких) стержней потеря устойчивости часто наступает при сравнительно небольших сжимающих напряжениях, не являющихся опасными с точки зрения прочности самого материала.
История развития строительного искусства знает немало случаев кру- шения инженерных сооружений из-за неправильного их расчета на устой- чивость. Так, например, в 1907 г. обрушился большой мост консольной сис-
145
темы с главным пролетом 549 м через реку Св. Лаврентия в США. Разруше- ние произошло во время строительства за 15 мин до конца рабочего дня, при этом все находившиеся на мосту рабочие и техники погибли (всего по- гибло 74 человека); 9 тыс. тонн металлических конструкций пришло в пол- ную негодность. Бόльшая часть конструкций затонула в воде, погрузившись в отдельных местах на глубину более 40 м.
Это грандиозное крушение Квебекского моста (мост строился в 14 км от Квебека) весьма поучительно. Причиной катастрофы явился неправиль- ный расчет сжатого составного стержня на устойчивость.
В то время теория расчета таких стержней не была в достаточной сте- пени разработана, что является извиняющим обстоятельством для проекти- ровщиков.
Интересно отметить, что спустя 9 лет, когда в 1916 г. завершились ра- боты по возведению нового Квебекского моста на том же месте и по той же схеме, произошло вторичное крушение, при котором упал в воду и затонул подвесной пролет.
Другой трагический случай, который может служить предметным уро- ком, доказывающим необходимость и важность тщательного расчета сжатых элементов на устойчивость, произошел с мостом у деревни Мен- хенштейн в Швейцарии в мае 1891 г. В момент катастрофы по мосту прохо- дил пассажирский поезд, состоявший из 12 вагонов. Мост имел небольшую длину – всего 42 м. Паровоз успел пройти через мост, но упавшие вагоны увлекли его за собой. Из 12 вагонов упало 6; падавшие друг на друга вагоны разбивались и образовывали груду обломков. При катастрофе погибло 74 и было ранено около 200 человек. Причина катастрофы заключалась в том, что один из сжатых раскосов фермы потерял устойчивость и повлек за со- бой разрушение всего моста.
Таким образом, продольный изгиб является опасным, его допускать нельзя. Поперечные сечения сжатых стержней должны назначаться не из условий прочности от чистого сжатия, а из условий того, чтобы сжи- мающие напряжения были меньше критических напряжений:
σ < σкр = Ркр 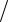 F .
F .
Определение критических сил, изучение форм потери устойчивости, разработка метода подбора сечений составляют основную задачу науки об устойчивости сооружений.
На рис. 14.2 показаны случаи потери устойчивости различных упру- гих систем. В сжатом стержне (рис. 14.2, а) при превышении силой крити- ческого значения может произойти выпучивание. Сжимающая сила вызы- вает, кроме сжатия, также изгибающие моменты. Кольцо (рис. 14.2, б) под гидростатическим давлением во всех сечениях испытывает центральное
146
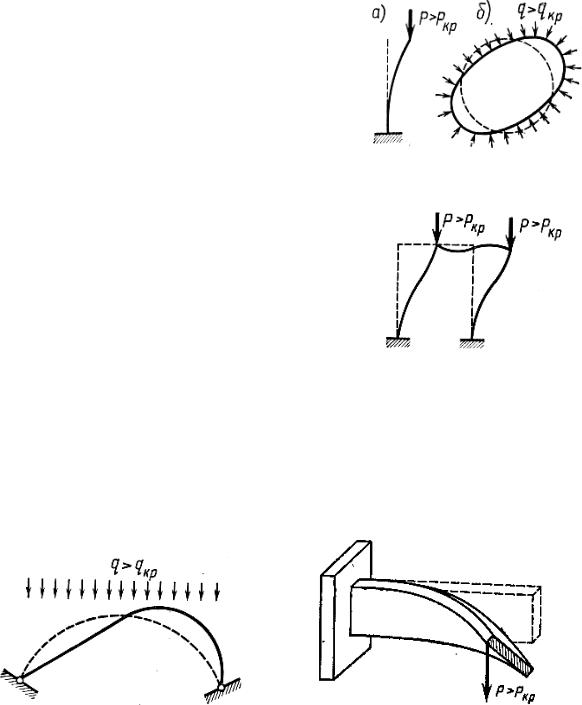
сжатие. Однако при некотором значении давления q > qкр круговое очерта- ние кольца перестает быть устойчивым. Кольцо изгибается и превращается в эллипс.
На рис. 14.3 показана рама, на которую действуют силы, приложенные в узлах. Эти си- лы вызывают центральное сжатие в стойках.
Как только силы Р превысят критиче- ское значение, рама мгновенно изогнется, уз- лы ее переместятся в сторону, произойдет по- теря устойчивости первоначально заданного равновесия рамы. Такая же картина происхо- дит с аркой (рис. 14.4).
Все изображенные на рис. 14.2 – 14.4 случаи характерны тем, что до потери устой- чивости во всех сечениях наблюдалось только центральное сжатие. В момент потери устой- чивости к центральному сжатию присоединя- ется изгиб. Система переходит из одного со- стояния равновесия в другое. Происходит по-
теря устойчивости центрального сжатия.
На рис. 14.5 показан другой случай поте- ри устойчивости. Вначале балка испытывает изгиб в вертикальной плоско-
сти (плоский изгиб). Как только сила превысит критическое значение, пло- ская форма изгиба становится неустойчивой, появляются дополнительный изгиб в горизонтальной плоскости и кручение. Аналогичным образом мо- жет произойти потеря устойчивости при кручении, внецентренном сжатии и при других видах деформации.
Рис. 14.4 |
Рис. 14.5 |
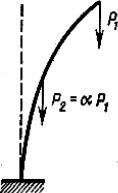
Если система загружена не одной, а несколькими силами или какой- либо сложной нагрузкой, то выбирается один параметр и вся система сил считается изменяющейся пропорционально этому параметру. Например, для стержня, загруженного двумя силами (рис. 14.6), сила Р2 выражена че-
147
|
рез P (P = αP ) с помощью множителя α. Таким обра- |
||
|
1 |
2 |
1 |
|
зом, Р1 принимается за параметр, с точностью до которо- |
||
|
го заданы все силы. Определив критический параметр |
||
|
Р1кр и зная α, можно найти всю критическую нагрузку |
||
|
для такого стержня. |
||
|
Вопросами устойчивости занимается специальная |
||
|
наука – « устойчивость сооружений». В курсе сопротив- |
||
|
ления материалов обычно рассматривается только одна |
||
|
наиболее простая задача об устойчивости прямолиней- |
||
|
ных сжатых стержней, представляющая собой как бы |
||
Рис. 14.6 |
введение в общую теорию устойчивости сооружений. |
||
14.2. Метод Эйлера для определения критических сил. Вывод формулы Эйлера
Для исследования устойчивости равновесия упругих систем имеется несколько методов. Основы и техника применения этих методов изучаются в специальных курсах, посвященных проблемам устойчивости различных объектов, встречающихся в строительстве и машиностроении.
Наиболее универсальным является динамический метод, основанный на изучении колебаний системы вблизи заданного положения равновесия. Однако в курсах сопротивления материалов он обычно не изучается по двум причинам: во-первых, его применение требует специальных знаний в области динамики упругих систем, а во-вторых, и это главное, подавляющее большинство задач, встречающихся в инженерной практике, может быть решено более простым методом – методом Эйлера.
Метод Эйлера основан на анализе разветвления возможных форм рав- новесия упругой системы. Рассмотрим его идею более подробно на примере центрально-сжатого, идеально прямого стержня. При малых сжимающих силах прямолинейная форма стержня является устойчивой. При больших силах, превышающих некоторое критическое значение, она является неус- тойчивой, а устойчивой будет криволинейная форма.
Таким образом, при Р > Ркр теоретически возможно существование двух форм равновесия. Наименьшее значение сжимающей силы, при кото- ром наступает разветвление форм равновесия, называется критической си- лой. Следовательно, при критической силе наряду с исходной прямолиней- ной формой как бы возможна смежная, весьма близкая к ней искривленная форма. По определению Эйлера, критической силой называется «сила, тре-
бующаяся для самого малого наклонения колонны». Желающим более под-
148
робно ознакомиться с этим вопросом рекомендуем книгу |
|
||||||||||
В. В. Болотина «Неконсервативные задачи теории упру- |
|
||||||||||
гой устойчивости» (Физматгиз, 1961). |
|
|
|
||||||||
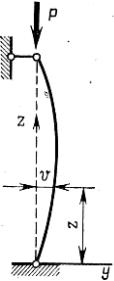
Для вывода формулы Эйлера рассмотрим шарнир- |
|
||||||||||
но-опертый, центрально-сжатый стержень постоянного |
|
||||||||||
сечения (рис. 14.7) в слегка отклоненном состоянии от |
|
||||||||||
прямолинейной формы. |
|
|
|
|
|
|
|
||||
Изгибающий момент в произвольном сечении равен |
|
||||||||||
M = Pv. |
|
|
|
|
|
|
|
||||
Дифференциальное уравнение изгиба стержня за- |
|
||||||||||
пишется в следующем виде: |
|
|
|
|
|
|
|
||||
|
d 2v |
|
= − |
|
M |
= − |
Pv |
, |
|
||
|
|
|
|
|
|
|
|||||
|
dz2 |
EJ |
EJ |
Рис. 14.7 |
|||||||
или |
|
|
|
|
|
|
|||||
|
|
|
d 2v |
+ k 2v = 0, |
(14.1) |
||||||
|
|
|
dz2 |
||||||||
|
|
|
|
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
||||
|
|
|
k 2 = |
P |
. |
|
|
(14.2) |
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
EJ |
|
|
|
|
Интеграл дифференциального уравнения (14.1) имеет вид |
|
||||||||||
|
v = Acos kz + B sin kz. |
(14.3) |
|||||||||
Для определения значений произвольных постоянных А и В используем граничные условия. Первое граничное условие: при z = 0 и v = 0 A = 0.
Следовательно, уравнение оси изогнутого бруса (14.3) примет вид
v = B sin kz. |
(14.4) |
Таким образом, стержень изгибается по синусоиде. |
|
Второе граничное условие: при z = l и v = 0 B sin kl = 0. |
Это условие |
выполняется в двух случаях: 1) В = 0; 2) sinkl = 0.
Первый случай нас не интересует, так как при В = 0 прогибы во всех точках равны нулю, следовательно, стержень остается прямым.
Второе условие sinkl = 0 дает kl = π, 2π, Зπ, ..., nπ, учтя значение k
(14.2), получим: |
|
|
|
|
|
|
|
|
|
P = |
π2 EJ |
; |
(2π)2 EJ |
; |
(3π)2 EJ |
; ... ; |
(nπ)2 EJ |
. |
|
|
2 |
l 2 |
l2 |
l2 |
|||||
кр |
l |
|
|
|
|
||||
|
|
|
|
|
|||||
Итак, получено не одно, а множество значений критических сил. Каж- дой критической силе соответствует своя форма равновесия (рис. 14.8). Подставляя найденное значение k в уравнение оси изогнутого бруса (14.4), замечаем, что при первой критической силе стержень изгибается по одной
149
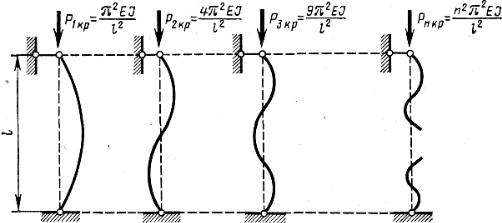
полуволне синусоиды, а при всех последующих число полуволн равно но- меру соответствующей критической силы.
Рис. 14.8
Интересно отметить, что равновесие, соответствующее первой форме изгиба, является устойчивым, а всем остальным – неустойчивым.
Для инженерных расчетов практический интерес представляет только наименьшая критическая сила
P = |
π2 EJ |
. |
(14.5) |
|
|
2 |
|||
кр |
l |
|
|
|
|
|
|
||
Эту формулу более двухсот лет назад (в 1744 г.) впервые получил Ле- онард Эйлер, поэтому ее называют формулой Эйлера, а определяемую этой формулой критическую силу часто называют эйлеровой силой.
Из формулы Эйлера видно, что величина критической силы прямо пропор- циональна жесткости и обратно пропорциональна квадрату длины стержня.
Для стержня, работающего в упругой стадии, критическая сила зави- сит только от геометрических размеров стержня и модуля упругости мате- риала, но совершенно не зависит от прочностных характеристик материала, из которого изготовлен стержень. Так, например, она не зависит от сорта стали. Для стали Ст. 3 и для высокосортной стали модули упругости прак- тически одинаковы, поэтому и критические силы также равны между собой. Два стержня с одинаковыми геометрическими размерами, но изготовленные из различных сталей и работающие в упругой стадии, теряют устойчивость при одной и той же критической силе.
Таким образом, выясняется резкая разница между работой стержня на сжатие и на растяжение. Предельная растягивающая сила непосредственно зависит от прочностных характеристик материала и потому различна для разных сортов стали, в то время как при сжатии в пределах упругости на- блюдается совершенно иная картина.
150
