scherbo-sp2

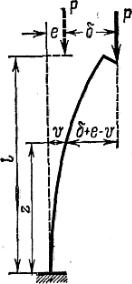
Не следует думать, что для выпучивания при силах, меньших Рr, тре- буются какие-то специальные условия по обеспечению нужного закона из- менения силы с увеличением прогиба. Требуется лишь, чтобы в начальный момент искривления стержня действующая на него нагрузка возрастала. Именно этот случай нагружения является характерным как в работе элемен- тов конструкций, так и при испытаниях стержней на центральное сжатие.

Итак, если центрально-сжатый стержень испытывает действие возрас- тающей нагрузки, то он имеет целый интервал значений силы

Pτ ≤ P ≤ Pr ,

в каждой точке которого может начаться искривление стержня, а наимень-

шей силой выпучивания является касательно-модульная сила Pτ. Заметим,

что качество равновесия стержня в точках Р = Рτ и Р = Рr различно, в связи с чем обсуждается вопрос о том, какую из этих сил надо считать или называть критической. Ответ на него во многом зависит от того, какой строгий смысл вкладывается в понятие критической нагрузки.

Разница в величине Pτ и Рr для реальных стержней обычно невелика, поэтому опытом весьма трудно проверить, при какой именно силе стержень теряет устойчивость. Этим, вероятно, и можно объяснить то, что описанное выше представление о касательно-модульной силе как о наименьшей воз- можной силе выпучивания для стержня в условиях возрастающей нагрузки долго оставалось незамеченным.

14.6. Расчет внецентренно-сжатой гибкой стойки

Большой познавательный интерес представляет задача о вне-центренном сжатии гибкого стержня, ра- ботающего в пределах упругих деформаций. Эта задача особенно интересна тем, что в ней наблюдается слож- ная нелинейная зависимость между напряжениями и сжимающей силой. Благодаря этому вопрос о прочно- сти такого стержня выделяется в особый класс задач, резко отличающихся от всех изученных ранее.

На рис. 14.17 показана внецентренно-сжатая стойка. Если стойка достаточно гибкая, то при опреде- лении изгибающих моментов нельзя пренебречь де- формациями стойки. Изгибающий момент в произволь- ном сечении определяется равенством

M = P(δ + e − v),

где е – эксцентриситет приложения силы Р;

Рис. 14.17

v – отклонение произвольной точки оси стержня по горизонтали.

161

Дифференциальное уравнение изгиба примет вид

d 2v = P(δ + e − v) , dz2 EJ x

или

d 2v + k 2v = k 2 (δ + e), dz2

где

k 2 = P . EJ x

В отличие от задачи центрального сжатия в этом случае получено неод- нородное уравнение. Интеграл этого уравнения состоит из двух слагаемых.

ничные условия. Угол поворота в заделке равен нулю, поэтому

Это уравнение удобнее решить относительно величины (δ + e). Для этого в правую часть добавим величину е и вычтем эту же величину. Реше-

cos kl

Теперь можно определить наибольший изгибающий момент в заделке:

162

M = P(δ + e) = Pe . (14.14)

max

cos kl

Наибольшее сжимающее напряжение в заделке при сжатии и изгибе равно

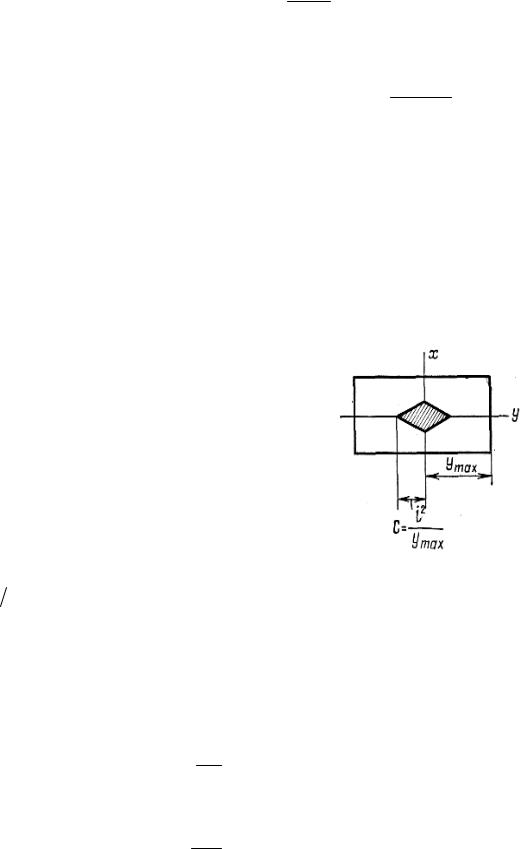
Величина с представляет собой расстояние от центра тяжести до крайней точки ядра сечения (рис. 14.18). Обозначим отношение эксцентри- ситета к расстоянию до крайней точки ядра сече-

ния через mе:

Из формулы (14.16) видно, что наибольшие напряжения во вне- центренно-сжатой гибкой колонне нелинейно зависят от силы Р. Для ана-

лиза этого вопроса на рис. 14.19 построен график изменения σmax в зависи- мости от силы Р. В целях большей наглядности воспользуемся понятиями метода допускаемых напряжений.

Обозначим отношение

[σT] = n,

σ

а отношение сил, которые соответствуют этим напряжениям,

PσT = n1.

P[σ]

163

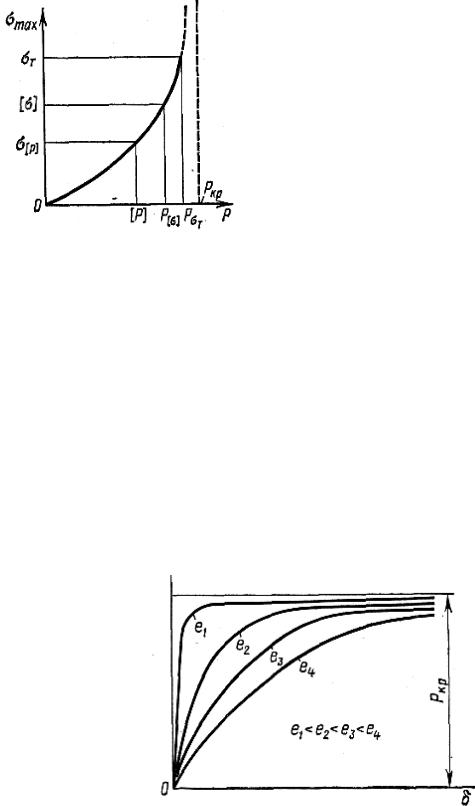
Из графика видно, что напряжения σТ и [σ] в большей степени отли- чаются друг от друга, чем силы PσT и Р[σ], поэтому n1 < n.

графика, показанного на рис. 14.19.

Рассмотренная задача убеждает нас в том, что работа сжатых элемен- тов существенно отличается от работы растянутых стержней. Именно то обстоятельство, что напряжения растут значительно быстрее, чем сжимаю- щая сила, является главной особенностью работы гибких внецентренно- сжатых стержней.

Уместно теперь поставить вопрос о том, в какой степени абсолютная величина эксцентриситета влияет на развитие деформаций сжатого стержня. Анализ этого вопроса показывает, что величина эксцентриситета е оказывает влияние на быстроту нарастания деформаций. Обратимся к графику, изобра- женному на рис. 14.20, где приведены кривые нарастания прогибов в зави- симости от величины эксцентриситета.

Р

Рис. 14.20

164

Этот график показывает, что чем больше начальный эксцентриситет, тем быстрее нарастают прогибы при нарастании силы Р. Вместе с тем можно отметить еще одну особенность: при малых эксцентриситетах кривая, описывающая нарастание прогибов, вначале близка к прямой, а когда сжи- мающая сила приближается к критической силе, происходит весьма интен- сивный рост деформаций.

Все сказанное говорит о том, что начальные эксцентриситеты могут оказывать большое влияние на прочность сжатых стержней.

Особенную опасность имеют случайные эксцентриситеты, которые предусмотрены в расчетах и не ожидались проектировщиком, а в действи- тельности имеют место из-за неучтенных причин.

Случайные эксцентриситеты могут привести к значительной пере- грузке, а в отдельных случаях – к гибели сооружения.

14.7. Практический расчет сжатых стержней

При назначении размеров сжатых стержней в первую очередь прихо- дится заботиться о том, чтобы стержень в процессе эксплуатации при дей- ствии сжимающих сил не потерял устойчивость. Поэтому напряжения в сжатом стержне должны быть обязательно меньше критических:

Fbrutto – площадь сечения брутто.

Исследования показали, что местные ослабления, например, закле- почные отверстия, ослабления за счет врубок и т. п. не оказывают сущест-

венного влияния на величину критической силы. Этим объясняется, что в формуле (14.17) при определении критических напряжений берется пло- щадь сечения брутто. В тех особых случаях, когда ослабления весьма зна- чительны, дополнительно производится проверка прочности по ослаблен- ному сечению на чистое сжатие.

Для надежной работы сжатого стержня необходимо предусмотреть определенный запас устойчивости, поэтому напряжения в стержне должны быть меньше расчетного сопротивления, которое в свою очередь должно составлять некоторую часть от критического напряжения:

где n1 – коэффициент запаса устойчивости.

165

Проведем сравнение формулы (14.18) с формулой, применяемой при подборе сечений растянутых стержней,

Величина ϕ представляет, собой коэффициент уменьшения основного расчетного сопротивления при продольном изгибе. В строительных нормах и правилах (СНиП II-B.3-62) он называется коэффициентом продольного изгиба. Коэффициент ϕ зависит от критического напряжения, а следова- тельно, является функцией гибкости стержня [см. формулу (14.9)]:

Значения величины коэффициента ϕ для различных гибкостей уста- новлены нормами и обычно приводятся в виде таблиц. Эти таблицы учиты- вают также зависимость ϕ от возможных эксцентриситетов.

В табл. 14.1 даны значения коэффициентов ϕ для центрально-сжатых стержней, взятые из СНиП II-В.3-62.

166

Для деревянных центрально-сжатых элементов:

Расчетная формула для сжатого стержня в форме (14.20) внешне сов- падает с формулой (а) для растянутого стержня. Такая запись удобна тем, что она позволяет пользоваться одним расчетным сопротивлением как для сжатых, так и для растянутых стержней.

Подбор сечения сжатых стержней представляет собой более сложную за- дачу, чем растянутых. Это объясняется тем, что величина ϕ, входящая в расчет- ную формулу, зависит от размеров и формы поперечного сечения и поэтому за- ранее не может быть назначена. Ввиду этого подбор сечения обычно проводят путем попыток. Вначале задаются примерными размерами поперечного сечения (или примерным значением ϕ, например, 0,5), и для этого сечения находят пло-

щадь, момент инерции, радиус инерции и затем гибкость:

λ = μl . i

На основании полученной гибкости по табл. 14.1 определяют величину ко- эффициента ϕ, а затем по формуле (14.20) находят напряжение. Естественно, что при первой попытке полученное напряжение может значительно отличаться от расчетного сопротивления. Если оно будет меньше расчетного сопротивления, то размеры нового сечения необходимо уменьшить и, наоборот, увеличить, если напряжение будет больше расчетного сопротивления.

Процесс последовательных попыток продолжается до тех пор, пока разница между σрасч и R не будет меньше той величины, которая установле- на СНиПом. Обычно требуется, чтобы разница в указанных напряжениях не превышала 3 – 5 %.

167

Пример

Подобрать двутавровое сечение из мостовой стали Ст. 3 центрально- сжатой колонны, заделанной одним концом при другом свободном конце. Расчетная сжимающая сила Р = 120 тс. Длина колонны l = 2,6м, Расчетное сопротивление R = 2100 кгс/см2.

Решение. Коэффициент приведенной длины для данного случая за- крепления концов стержня (см. п. 14.3) m = 2. Подбор сечения проводим пу- тем последовательных приближений.

Приближение 1. Принимаем в первом приближении j = 0,5, тогда из условия

Так как напряжение больше расчетного сопротивления, то увеличива- ем сечение колонны.

Приближение 2. Принимаем двутавр № 60. Для него F = 132 см2, i = 3,60 см,

l = 2 × 260 = j =

144; 0,34;

3,60

следовательно,

s = 120000 = 2674 кгс/см2 > 2100 кгс/см2 , 0,34 ×132

поэтому вновь увеличиваем сечение.

Приближение 3. Принимаем двутавр № 65, для которого

F =153см2 , imin = 3,77 см.

Далее находим

l = 2 × 260 = 2120кгс/см2 » 2100 кгс/см2. 3,77

Так как напряжение практически совпало с расчетным сопротивлени- ем, то на этом задачу подбора сечения заканчиваем. Таким образом, оконча- тельно принимаем двутавр № 65.

168

М-15. ДИНАМИЧЕСКОЕ ДЕЙСТВИЕ НАГРУЗОК

15.0. Введение в модуль

Модуль содержит следующие структурные элементы:

1.Общие замечания.

2.Учет сил инерции при расчете троса.

3.Расчеты на удар.

4.Собственные колебания системы с одной степенью свободы.

5.Вынужденные колебания упругой системы.

Цель модуля – изучить методику расчета прочности при ускоренном движении, периодической нагрузке, ударе.

15.1. Общие замечания

Во всех предыдущих главах курса рассматривалось действие статиче- ской нагрузки, которая прикладывается к сооружению настолько медленно, что возникающие при этом ускорения движения частей сооружения весьма малы, и поэтому их можно не учитывать.

Часто в инженерной практике приходится встречаться с так называе- мой динамической нагрузкой, которая сравнительно быстро меняет свою величину или положение (например, движущийся поезд). Динамическая на- грузка вызывает колебательное движение частей сооружения. Поэтому при расчете необходимо учитывать силы инерции, зависящие как от массы са-

мого сооружения, так и от массы нагрузки (например, массы поезда).

С силами инерции в свою очередь связаны дополнительные напряже- ния и деформации. Иногда эти дополнительные напряжения весьма велики и могут даже превышать напряжения от основных сил.

На практике влияние динамической нагрузки, как правило, учитыва- ется с помощью так называемого динамического коэффициента. Для полу- чения максимального значения усилия динамическая нагрузка заменяется статической, а найденное от нее усилие или перемещение помножается на динамический коэффициент:

S Д = μ SСТ .

Динамический коэффициент μ во многих случаях определяют анали- тически, а в тех случаях, когда это сделать трудно, – экспериментально. Ес- тественно, что этот коэффициент зависит от вида динамической нагрузки, от размеров, массы, жесткости сооружения и от других факторов.

В общем случае динамическая нагрузка представляет собой очень сложное воздействие на сооружение, которое не всегда можно учесть.

В курсе сопротивления материалов обычно рассматривают лишь про- стейшие задачи и при их решении часто применяют ряд вспомогательных гипотез, облегчающих расчет. Ограничимся здесь рассмотрением лишь сле-

169

дующих расчетов: расчета каната при подъеме груза; расчета на удар и ко- лебания системы с одной степенью свободы.

15.2. Учет сил инерции при расчете троса

Рассмотрим расчет троса при подъеме груза весом G с ускорением а (рис. 15.1). Вес 1 м троса обозначим q. Если груз неподвижен, то в произ- вольном сечении каната mn возникает статиче- ское усилие от веса груза и каната, определяемое из условия равновесия нижней отсеченной части:

NСТ = G + qz.

При подъеме груза с ускорением а для оп- ределения натяжения каната необходимо состав- лять уравнение движения груза. Для этой цели в сопротивлении материалов используют извест- ный из теоретической механики принцип Далам- бера. Согласно этому принципу движущуюся систему можно рассматривать как находящуюся в равновесии, если ко всем точкам ее присоединить дополнительно силы инерции.

Сила инерции численно равна произведе- нию массы на ее ускорение и направлена в сторону, противоположную ус- корению.

С помощью принципа Даламбера любая динамическая задача по фор- ме решения сводится к более простой (статической) – составлению уравне- ний равновесия.

В нашей задаче, для которой составляется уравнение равновесия, сум- марная сила инерции равна

или

N Д = μNСТ .

Динамическое напряжение равно

σ Д = N Д = μσСТ .

F

Величина динамического коэффициента определяется выражением

170