scherbo-sp2

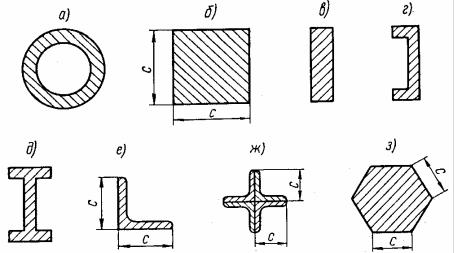
Задания для самостоятельной работы

Решить следующие задачи:

Задача 1

В направлении какой оси, расположенной в плоскости поперечного сечения, будет выпучиваться при потере устойчивости каждый из стерж- ней, сечения которых показаны на рис. 16.4, если каждый конец стержня одинаково закреплен во всех направлениях.

Рис. 16.4

Задача 2

Определить критическую силу для деревянной стойки прямоуголь- ного сечения размером 10 × 20 cм и длиной 8 м в следующих случаях:

а) оба конца стойки шарнирно закреплены; б) оба конца стойки защемлены;

в) один конец стойки защемлен, а другой свободен. Модуль упругости Е =104 МПа.

Ответ: а) Fкр= 26 кН; б) Fкр= 104 кН; в) Fкр= 6,5 кН.

Задача 3

Определить критическую силу для стального равнобедренного угол- ка с размерами сечения 100 ×100 ×10 мм и длиной 1,2 м при защемленном одном конце и свободном другом. Модуль упругости Е = 2 ×105 МПа.

Ответ: Fкр= 254 МПа.

Задача 4

Определить размеры поперечного сечения деревянной стойки дли- ной 7,5 м, защемленной обоими концами и сжатой силой Р = 262 кН. По- перечное сечение стойки квадратное. Основное допускаемое напряжение

[σ] = 10 МПа.

Ответ: 20 × 20 cм.

271

ТЕМА 17

Расчет составных стержней на устойчивость

Цель занятия: изучить методику расчета составных стержней на ус- тойчивость.

При расчетах составных стержней определение гибкости произво- дится несколько иначе:

а) составные элементы из уголков, швеллеров и т.п., соединенные вплотную или через прокладки, рассчитываются как сплошностенчатые (монолитные), при условии, что наибольшие расстояния между их соеди- нениями (прокладками и т. п.) не превышают 40i, где i – радиус инерции одного уголка или швеллера относительно центральной оси, параллельной плоскости расположения прокладок. В пределах элемента должно быть не менее двух прокладок.

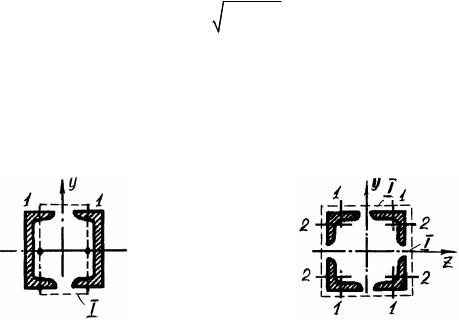
б) для стержня из двух швеллеров (двутавров), соединенных планка- ми I (рис. 17.1, а) надо сопоставить гибкость λz относительно «материаль- ной оси», т. е. оси, пересекающий элементы сечения, и приведенную гиб- кость λпр относительно «свободной оси» (не пересекающей элементов се- чения) и вести расчет по большей из них. Приведенная гибкость вычисля- ется по формуле

ду приваренными планками (в свету) или между центрами крайних за- клепок.

а) б)

Рис. 17.1

Желательно выбирать расстояние между швеллерами (двутаврами) так, чтобы соблюдалось условие равноустойчивости λх = λпр .

272

Для стержня из четырех уголков (рис. 17.1, б), у которого обе глав- ные центральные оси «свободные», расчет надо вести по большей из при- веденных гибкостей, вычисляемых по формуле

где λ – наибольшая гибкость всего стержня (λх и λу); λ1, λ2 – гибкости отдельных ветвей относительно осей 1 и 2, опреде-

ляемые так же, как и для стержня из швеллеров.

Целесообразно, чтобы приведенные гибкости относительно обеих главных центральных осей были одинаковыми.

Гибкость отдельной ветви (для обоих рассмотренных типов составных стержней) на участке между планками (λ1 , λ2) должна быть не более 40.

Пример 1

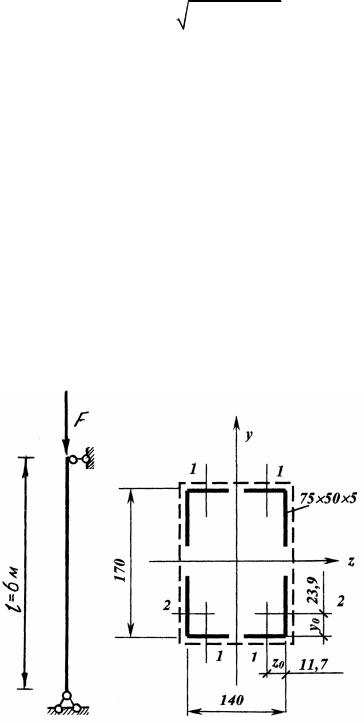
Определить допускаемую величину центральной сжимающей силы для стойки из четырех соединенных планками неравнобоких уголков 75×50×5 (рис. 17.2). Материал уголков сталь Ст. 3, R = 210 МПа .

Расстояние между планками выбирать так, чтобы максимальная гиб- кость ветви в плоскостях, параллельных планкам, не превышала 40. Опреде- лить коэффициент запаса устойчивости при предельной расчетной нагрузке.

Рис. 17.2

273

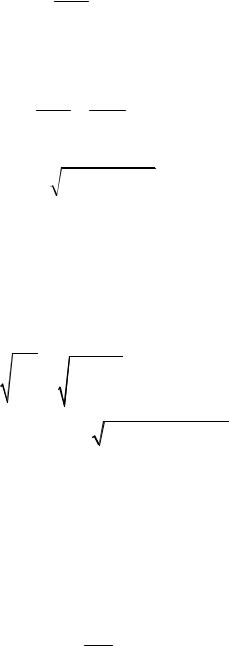
у0 = 2,39 см, z0 = 1,17 см.

Расстояние между планками (длина ветви) определяется по гибкости λ ≤ 40 относительно оси 1.

l1 = ℓвст = 40 , i1

откуда ℓвст = 40i1 = 40 ×1,43 = 57,2 см=572 мм .

При таком расстоянии между планками гибкость

l2 = ℓвст = 57, 2 = 24 . i2 2,39

Приведенная гибкость стержня (17.1)

lпр = l2 + l12 + l22 .

Вданном случае очевидно, что гибкость всего стержня, рассматривае- мого как монолитный, максимальна относительно оси у, т. е. λ = λ у .

Момент инерции всего сечения относительно оси у

На основании формулы (7.15) расчетное усилие в сжатой стойке

N = mjRA ,

где j = 0,52 (определен по таблице).

N =1×0,52 × 21× 4 ×6,11 = 266,9 кН ;

N = F = 266,9 кН.

Коэффициент запаса устойчивости

= σкр

ny jR .

λкр > λпред , следовательно, формула Эйлера применима.

274

Задания для самостоятельной работы

Решить следующую задачу.

Задача

Определить допускаемую величину центральной сжимающей силы для равноустойчивой стойки, состоящей из двух швеллеров № 20 с шар- нирным закреплением по концам. Высота стойки l = 5 м. Материал швел-

леров сталь Ст. 3, R = 210 МПа.

ТЕМА 18

Продольно-поперечный изгиб

Цель занятия: изучить методику проверки на прочность и устойчи- вость при продольно-поперечном изгибе.

Наибольшие и наименьшие нормальные напряжения в поперечном сечении балки с шарнирно закрепленными концами и сечением с двумя осями симметрии при продольно-поперечном изгибе и сжимающей силе S равны

σ = − S A ± M = − S ± M ± S y .

W A W W

Для материалов, одинаково сопротивляющихся растяжению и сжа- тию, условие прочности по методу допускаемых напряжений имеет вид

σ max ≤ [σ].

Для материалов, различно сопротивляющихся растяжению и сжатию, при расчете по методу допускаемых напряжений условия прочности мож- но записать так:

max σ p ≤ [σ p ] и max σc ≤ [σc ].

При расчете по предельным состояниям структура формул условной прочности остается такой же, только вместо допускаемых напряжений бу- дут соответствующие расчетные, а нормальные напряжения определяются при действии расчетных нагрузок.

Сжато-изогнутые стержни, кроме расчета на продольно- поперечный изгиб, необходимо рассчитывать также и на устойчивость,

так как, например, продольно-поперечный изгиб балки может происходить

ввертикальной плоскости, а искривление балки при потере устойчивости –

вгоризонтальной.

275

Полный прогиб при продольно-поперечном изгибе определяется по формуле

Следует отличать Эйлерову силу FЭ от критической Fкр, вычисляемой по формуле Эйлера. Значение Fкр можно вычислять по формуле Эйлера лишь при условии, что гибкость стержня больше предельной, значение же

= π2 EJ FЭ l2

вычисляется независимо от гибкости балки.

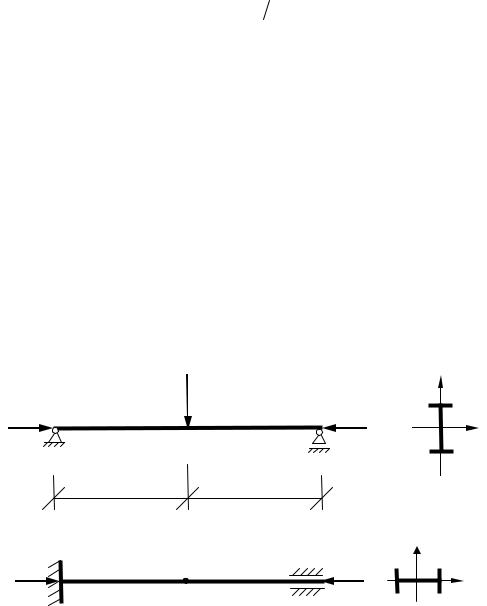
Рассмотрим пример решения задачи на продольно-поперечный изгиб. Двутавр № 36 длиной l = 5 м, концы которого в плоскости наиболь-

шей жесткости закреплены шарнирно, а в плоскости наименьшей жестко- сти защемлены, нагружен продольными сжимающими силами S = 700 кН и поперечной силой F = 25 кН, приложенной посередине пролета (рис. 18.1).

Проверить прочность и устойчивость двутавра, если [σ] = 160 МПа.

Рис. 18.1

1. Проверка устойчивости в плоскости наименьшей жесткости.

По сортаменту двутавр № 36 имеет площадь поперечного сечения

Так как концы двутавра в этой плоскости защемлены, то коэффициент приведения длины μ = 0,5, а величина жесткости λ равна

276

l = ml = 0,5 ×500 =

86,5.

imin 2,89

Коэффициент снижения допускаемого напряжения j определим из

Допускаемое значение усилия S

[S ] = j×[s]× A = 0,711×61,9 ×16 = 704,2 кН » S = 700 кН.

Устойчивость в плоскости наименьшей жесткости обеспечена. 2. Проверка прочности в плоскости наибольшей жесткости. Используем приближенное решение.

Величина прогиба y0 от действия только поперечной нагрузки может быть определена либо с использованием метода начальных параметров, либо по методу Мора с использованием правила Верещагина.

Значение y0 равно

Наибольший прогиб с учетом сжимающей нагрузки равен

Максимальными по модулю будут сжимающие напряжения

Прочность балки в плоскости наибольшей жесткости обеспечена.

277

Задание для самостоятельной работы

Решить следующую задачу.

Задача

Стальной стержень прямоугольного поперечного сечения b×h =12×30 см длиной 5 м с шарнирным закреплением по концам в двух плоскостях на- гружен в плоскости наибольшей жесткости равномерно распределенной нагрузкой q = 15 кН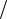м и продольной сжимающей нагрузкой S = 900 кН.

Проверить прочность и устойчивость стержня. Нагрузки – норматив- ные, [σ] = 160 МПа.

ТЕМА 19

Инерционные нагрузки

Цель занятия: изучить методику расчета брусьев на действие инер- ционных нагрузок.

При ускоренном движении частей конструкции в них возникают до- бавочные вполне реальные напряжения, которые эквивалентны статиче- ским напряжениям, вызванным силами инерции; от каждого элемента стержня на соседние части материала будут передаваться такие напряже- ния, как будто бы к нему была приложена соответствующая сила инерции.

Отсюда получаем практическое правило для определения напряже- ний в части конструкции, точки которой испытывают ускорения: надо вы- числить эти ускорения и в дополнение к внешним силам, действующим на рассматриваемый элемент конструкции, нагрузить его соответствующими силами инерции. Дальше следует вести расчет так, как будто на стержень действует статическая нагрузка.

Это справедливо для случая, когда величина и расположение внеш- них сил, приложенных к рассматриваемому элементу, не зависят от его деформаций; если эти деформации не изменяют характера движения стержня, то ускорения его точек вычисляют по правилам кинематически твердого тела и учет динамических воздействий сводится к добавочной статической нагрузке соответствующими силами инерции.

Рассмотрим расчет на действие инерционных нагрузок с помощью конкретных примеров.

Пример 1

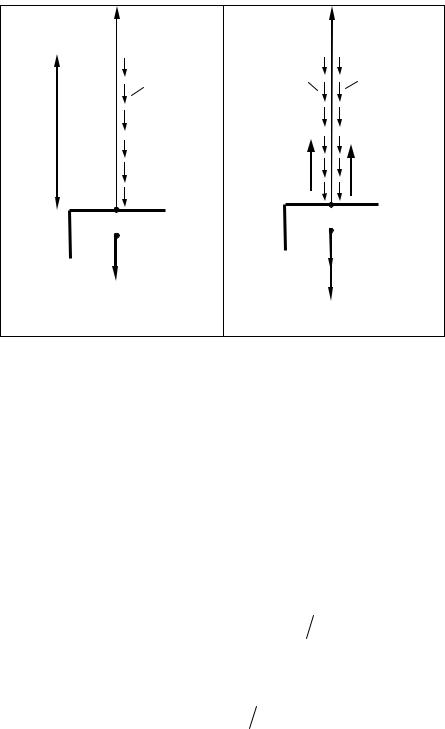
Груз массой 3 т поднимается равноускоренно с помощью стального троса, причем за первые две секунды он поднимается на высоту 4 м. Пло- щадь поперечного сечения троса 5 см2, длина его 90 м, объемный вес 72 кН/м3. Определить наибольшее нормальное напряжение в тросе без уче- та и с учетом его собственного веса (рис. 19.1).

278

Рис. 19.1

Величина продольной силы в произвольном сечении каната при ста- тическом нагружении без учета собственного веса

Nст = G = mg = 3000 ×9,8 = 29400 H = 29,4 кН;

279

Нормальные напряжения с учетом сил инерции можно определить по формуле

sд = Nд ;

A

б) определить значение динамического коэффициента

kд =1+ a , g

а тогда

sд = sст × kд; Nд = Nст × kд.

Воспользуемся вторым методом, но для этого необходимо опреде- лить величину ускорения

Величина динамических напряжений без учета собственного веса троса будет равна:

sд = sст × kд = 58,8 ×1,204 = 70,8 МПа.

Максимальная величина динамических напряжений с учетом собст- венного веса троса

max sд = max sст × kд = 65,28 ×1, 204 = 78,6 МПа.

Пример 2

Ломаный стальной стержень постоянного поперечного сечения диа- метром 20 мм и размерами, показанными на рис. 19.2, вращается с посто- янной угловой скоростью. Определить допускаемое число оборотов стержня, если [σ] = 160 МПа.

Собственный вес можно не учитывать.

Приложив к системе силы инерции, мы переходим к решению стати- ческой задачи (рис. 19.2, б).

Интенсивность сил инерции зависит от расстояния до оси вращения и равна

280