Добавил:

kane4na kane4na@yandex.ru Полоцкий Государственный Университет (ПГУ), город Новополоцк. Что бы не забивать память на компьютере, все файлы буду скидывать сюда. Надеюсь эти файлы помогут вам для сдачи тестов и экзаменов. Учение – свет. Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Полоцкий Государственный Университет

Предмет:

Сопротивление материалов

Файл:

scherbo-sp2

.pdf

Скачиваний:

Добавлен:

24.01.2023

Размер:

12.06 Mб

Скачать

☆

<<< < Предыдущая 14 15 16 17 18 19 20 21 22 23 24 2526 / 3826 27 28 29 30 31 32 33 34 35 36 37 38 > Следующая >>>

W =

bh2

b(1,5b)2

= 0,375b3; W

hb2

1,5b ×b2

= 0,25b3.

s =

3000

1000

12000

;

0,375b3

0,25b3

τ = 0. sIII

= s =

12000

1экв

Точка 2.

Му

1000

4000

. t

; W = bb3.

0, 25b3

При

=1,5 β = 0,346,

γ = 0,859.

W = 0,346b3 t

3000

;

0,346b3

s2IIIэкв =

s22 + 4t22 ;

17796

s2IIIэкв

40002 + 4 ×8670,52

Точка 3.

s3 =

M z

3000

8000

;

0,375b3

= gt

= 0,859 ×

8670,5

7448

max

16908

sIII

+ 4t2

80002 + 4 ×74482

3экв

Наиболее опасной оказалась точка 2 с s2IIIэкв

17796

Условие прочности

smaxэкв

£ [s];

17796

£16.

b = 3

17796

= 3

»10,5 cм ;

1112, 25

h =1,5b =1,5 ×10,5 =15,75 см.

Задания для самостоятельной работы

Самостоятельно решить следующие задачи.

Задача 1

В опасном поперечном сечении вала действуют изгибающие момен- ты M z = 25 кНм, М у = 16 кНм и крутящий момент Tк = 15 кНм. Проверить

на прочность:

251

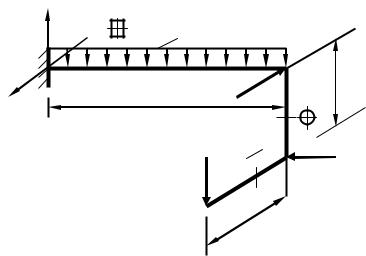
а) стержень с круглым поперечным сечением диаметром d = 120 м ; б) стержень с прямоугольным поперечным сечением b × h =120×180 мм,

нагрузки – нормативные, [σ] = 100 МПа.

Задача 2

В опасном сечении вала кольцевого круглого сечения с соотношени-

ем диаметров	d	= 0,8 действует изгибающий момент	Mи = 40 кН×м и

	D
крутящий Тк = 50кН×м.
Определить требуемые размеры поперечного			сечения, если
[σ] = 80 МПа.

ТЕМА 14

Расчет пространственного ломаного бруса

Цель занятия: изучить методику определения внутренних усилий и расчета на прочность пространственных брусьев.

В основе определения внутренних усилий лежит метод сечений с ис- пользованием локальных (местных) систем координат для каждого участ- ка. В общем случае каждый участок ломаного бруса может работать на со- вокупность различных видов деформаций, а для определения размеров по- перечных сечений используются и теории упругости.

Рассмотрим расчет пространственного ломаного стержня на кон- кретном примере. Расчетная схема бруса изображена на рис. 14.1

2 кН/м

А		4 кН

4 м

4 кН

	В
	2 м
	d
d	3 кН
	С

2 м

Рис. 14.1

252

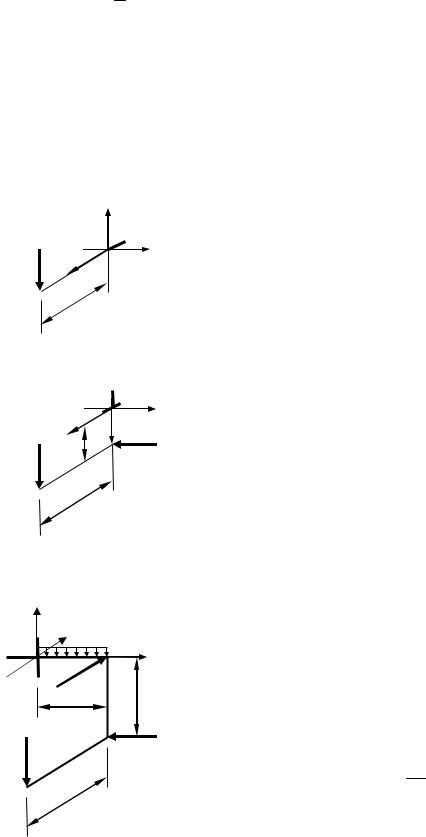
На участке АВ брус имеет прямоугольное поперечное сечение с со-

отношением сторон h = 2; на участках ВС, СD – круглое поперечное сече- b

ние диаметром d.

Требуется определить размеры поперечных сечений, если расчетное сопротивление материала R = 210 МПа .

1. Запишем аналитические выражения для внутренних усилий по уча- сткам ломаного бруса и определим их значение в характерных сечениях.

Правило знаков такое же, как при расчете на простые виды деформа-

ций.

		y
4 кНx		С

D х

	В
	y
4 кН	С х
	x
D	2 м

Участок DC 0 ≤ x ≤ 2 м

N = 0; Qy = -4 кН; Qz = 0

Участок СВ

3 кН

Tк = Мх = 0; M y = 0; M z = -4x.

x = 0, M z = 0; x = 2 м, M z = -8 кНм.

0 ≤ x ≤ 2 м

N = 4 кН; Qy = 0; Qz = -3 кН.

Тк = Мх = 0; M z = -4 × 2 = -8 кНм;

M y = -3x.

При x = 0 M y = 0;

при x = 2 м M y = -6 кНм.

Участок ВА

	y
	z	4 кН/м
		4 кН/м
		В	х
	4 кН
	x	м
	x	2
		2
	4 кН	С	3 кН
	4 кН
D	2 м

0 ≤ x ≤ 4 м

N = -3 кН; Qy = 4 + 2x;

x = 0, Qy = 4 кН; x = 4 м, Q =12 кН.

Qz = -4 кН.

Тк = Мч = -4 × 2 = -8 кНм.

M y = 4x. При x = 0 M y = 0;

при x = 4 м M y =16 кНм.

M z = -3 × 2 - 4x - 4 x2 = -6 - 4x - 2x2. 2

При x = 0 M z = -6 кНм; при x = 4 м M z = -22 кНм.

253

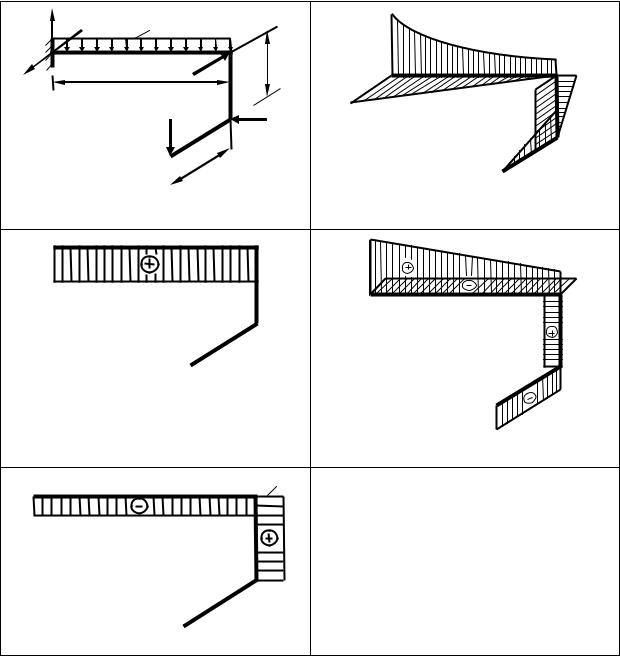
2. На основании выполненных расчетов строим эпюры внутренних усилий (рис. 14.2).

	2 кН/м
А		4 кН
А	4 м
	4 м
			4 кН
	D		2 м
	D		2 м

а)

в) Эп Tk (Mx) в кНм

д) Эп N (кН)

			22
В	м		6
	м
	2
	2	16
		16	8
			8
3 кН			8
С			8
			8

б) Эп Mz, My (кНм)

	12	4
	8	4
	8	4
	4	4
	4	3
		3
		3
		4
		4
	г) Эп Qy, Qz (кН)
	4

Рис. 14.2

3. Определим необходимый диаметр круглого поперечного сечения. На участке DC стержень подвергается прямому поперечному изгибу, а на

участке СВ –			изгибу в двух плоскостях и растяжению. Наиболее опасным
сечением для				стержней DC и СВ является сеч. В на участке СВ, где
	M z	= 8 кНм,		M y	=6 кНм и N = 4 кН.

254

Для брусьев круглого поперечного сечения можно определить сум- марный изгибающий момент

Mи = M z2 + M y2 = 82 + 62 =10 кНм.

Опасная точка при изгибе будет на поверхности бруса, а при растяже- нии напряжение во всех точках поперечного сечения одинаковы и равны

s =

pd 2

Следовательно, и при совместном действии изгиба и растяжения

опасная точка также будет на поверхности сечения.

Условие прочности при растяжении и изгибе бруса круглого попе-

речного сечения можно записать так:

smax =

Mи

32Mи

£ R.

Wz A

pd 3

pd 2

После подстановки значений Mи и N и решения кубического уравне- ния определяется необходимое значение диаметра круглого поперечного сечения. Для облегчения процедуры решения можно пренебречь влиянием продольной силы и подобрать размер d только из условия прочности на из- гиб, несколько округлив его значение в большую сторону, а затем прове- рить условие прочности с учетом продольной силы

32Mи

» R.

pd 3

d = 3

32Mи

32 ×1000

= 7,86 см » 8 см=80 мм.

3,14 × 21

s max =

32 ×10 ×100

4 × 4

=19,904 + 0,080 =

3,14 ×83

3,14 ×82

=19,984 кН

см

=199,84 МПа < R = 210 МПа.

Окончательно принимаем размер d = 80 мм.

4. Определим размеры прямоугольного поперечного сечения на уча- стке АВ. Наиболее опасным сечением будет сеч. А у жесткой заделки. Этот участок подвержен деформациям растяжения, кручения и изгиба в двух плоскостях.

Эпюры напряжений в этом опасном сечении изображены на рис.

14.3.Наиболее опасными точками в опасном сечении будут точки 1, 2, 3.

Вточке 1 будут максимальные сжимающие напряжения

s(1) = -	M	z	-	M y	-	N		τ(1) = 0.
							;
				Wy
	Wz					A

255

W =

bh2

b ×(2b)2

2b3

hb2

2b ×b2

;

A = b × h = b × 2b = 2b2.

s(1)

= - 3 × 22 ×100

- 3×16 ×100

= - 8100

- 1,5 .

2b3

2b2

s(1)III экв

= 8100 + 1,5 .

Эп σN

Эп σ M z

γτmax

M z

τmax

M z

γτmax

M y

Эп σ

M y

Рис. 14.3

В точке 2 будут максимальные касательные напряжения и нормаль- ные напряжения от My и N.

s(2)

= -

M y

= -

3×16 ×100

1,5

= -

4800

1,5

;

= tmax

Tк

Wк

Для прямоугольного поперечного сечения момент сопротивления кручению Wк определяется по формуле

Wк = ahb2.

При отношении hb = 2 находим значения α = 0, 246 , тогда

Wк = 0,246 × 2b ×b2 = 0,492b3.

256

		t2 =		800			=		1626				.
		t2 =	0, 492b3				=						.
			0, 492b3							b3
Эквивалентное напряжение по третьей теории прочности в точке 2
равно

					4800						1,5			2		1626			2
s(2)III	экв = s(2)2 + 4t(2)2			=	4800					+	1,5			2	+ 4	1626			2
																			.
						b		3				b	2				b	3	.
						b						b					b

Если пренебречь влиянием продольной силы, то

5798

s(2)III

экв

48002 + 4 ×16262

В точке 3 возникают нормальные напряжения от изгибающего мо-

мента Мz и продольной силы N и касательные от Тк.

s(3) = -

M z

= -

3× 2200

= -

3300

1,5

;

2b2

2b3

t(3) = gtmax = 0,79 ×

1626

1284,5

;

Эквивалентное напряжение по третьей теории прочности в точке 3

равно

3300

1,5

1284,5

s(3)III экв = s(3)2

+ 4t(3)2

Если пренебречь влиянием продольной силы, то

4182,1

s(3)III экв »

33002 + 4 ×1284,52

Сравнивая значения эквивалентных напряжений в точках 1, 2, 3, оп-

ределяем самую опасную точку.

Самой опасной точкой является точка 1, где

sIIIэкв

8100

1,5

8100

Из условия прочности sэквIII

£ R определим необходимый размер b:

b = 3

8100

» 7,3 см.

Проверим напряжение с учетом продольной силы

sэквIII =

8100

1,5

= 20,822 + 0,028 = 20,85 кН см2

= 208,5 МПа < R = 210 МПа.

7,33

7,32

Прочность обеспечена.

Окончательно принимаем b = 7,3 см,

h = 146 cм.

257

Задания для самостоятельной работы

Самостоятельно решить следующие задачи.

Задача 1

Для ломаного пространственного бруса (рис. 14.4) с постоянным круглым поперечным сечением построить эпюры внутренних усилий и оп- ределить необходимый диаметр d поперечного сечения. Нагрузки расчет- ные. R = 210 МПа.

3 м
	20 кН
		3 кН
1,5 м
4 кН
2 м		2 м
2 м	2	кН
	2	кН

Рис. 14.4

Задача 2

Для ломаного пространственного бруса (рис. 14.5) с постоянным квадратным поперечным сечением построить эпюры внутренних усилий и определить необходимый размер поперечного сечения. Нагрузки расчет- ные. R = 210 МПа.

5 м

2 кН/м

5 кН

2 м

6 кН

Рис. 14.5

ТЕМА 15

Тонкостенные стержни

Цель занятия: изучить методику определения геометрических характе- ристик поперечных сечений тонкостенных стержней, а также напряжений.

Рассмотрим порядок определения геометрических характеристик и напряжений на конкретных примерах.

258

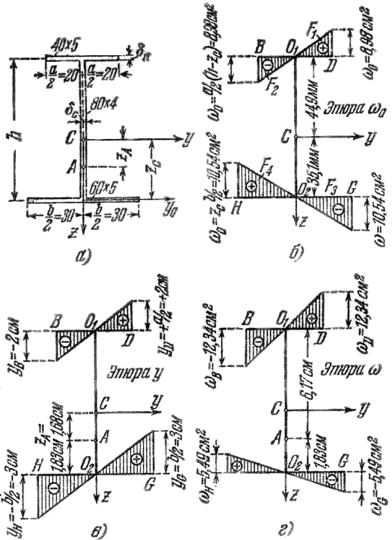
Пример 1

Для профиля, изображенного на рис. 15.1, а, определить положение центра изгиба, построить эпюру главных секториальных координат и вы- числить величину секториального момента инерции.

Рис. 15.1

Решение. Так как сечение симметрично относительно оси z, то центр тяжести С и центр изгиба А будут лежать на этой оси. Расстояние zC центра

тяжести сечения от средней линии нижней полки равно
z =	S y	=	-4 ×0,5 ×8 - 8 ×0, 4 × 4			= -	28,8	= -3,51
	0								см.
									см.
C	F		4 ×0,5 + 8 ×0, 4 + 6 ×0,5				8,2
	F		4 ×0,5 + 8 ×0, 4 + 6 ×0,5				8,2
Для нахождения расстояния zА от центра тяжести сечения С до цен-
тра изгиба А воспользуемся формулой
			zA = -	Sω y
				0	,
				J z	,
				J z

259

где Sω0 y – секториально-линейный статический момент сечения относи-

тельно полюса С и главной центральной оси инерции у, а Jz – момент инерции сечения относительно главной центральной оси инерции z. При- нимая за начало отсчетов точку O1, строим вспомогательную эпюру секто- риальных площадей w0 (см. рис. 15.1, б).

Секториально-линейный статический момент Sω y определяется из
	0
выражения
Sω y = ∫ w0 y dF = ∫ w0 ydn dy;
0
F	F

интеграл может быть вычислен по способу Верещагина путем умножения площадей эпюры w0 на ординаты эпюры расстояний у (см. рис. 15.1, в), лежащие под центрами тяжести площадей. Для правой половины верхней полки площадь эпюры w0 положительна и равна


F =	1	(h - z ) ×			a		×	a	=			h − zC	a2 ,
F =		(h - z ) ×					×		=				a2 ,
1	2		C		2			2	8
	2				2			2	8
а ордината эпюры у под центром тяжести площади F1 положительна и равна
		y =		2	×	a		=		a	;
		y =			×			=			;
		1	3		2				3
			3		2				3

таким образом,

Sω¢ 0 y = a3 (h - zC )dП . 24

Для левой половины верхней полки

F = -			1	(h - z )a2					,
F = -				(h - z )a2					,
2	8						C
	8
а ордината
	y2			= -		a	,
	y2			= -		3	,
						3
так что
S¢¢	=	a3			(h - z			)d		.
S¢¢	=				(h - z			)d	П	.
ω0 y	24						C		П
	24

Аналогично этому для правой и левой половин нижней полки находим

S¢¢¢	= S IV	= -	b3	z d		.
					П
ω0 y	ω0 y	24		C

Полная величина секториально-линейного статического момента равна

Sω y = 2(Sω¢				y	+ Sω¢¢¢	y ) = δП a3 (h - zC ) - b3 zC					=
0		0			0	12
	0,5			3		3						5
=			4		×(8 -	3,51) - 6	×	3,51	= -19,62	см			.
=	12		4		×(8 -	3,51) - 6	×	3,51	= -19,62	см			.
	12

260

<<< < Предыдущая 14 15 16 17 18 19 20 21 22 23 24 2526 / 3826 27 28 29 30 31 32 33 34 35 36 37 38 > Следующая >>>

Соседние файлы в предмете Сопротивление материалов

#
01.06.202211.08 Mб5scherbo-sp1.pdf
#
24.01.202312.06 Mб5scherbo-sp2.pdf
#
24.01.2023497.82 Кб5Лекция Внецентренное сжатие.pptx
#
01.06.2022711.68 Кб4Лекция Геометрические характеристики.pptx
#
24.01.2023451.06 Кб7Лекция Косой изгиб.pptx
#
01.06.20221.2 Mб8Лекция Кручение.pptx
#
01.06.2022639.54 Кб6Лекция Напряженное состояние.pptx