4)работа, совершаемая падающим телом, полностью преобразуется
вэнергию деформации конструкции.
В зависимости от направления удара по отношению к оси стержня и характера возникающих деформаций удар может быть: продольным (рас- тягивающим или сжимающим), поперечным (изгибающим) и крутящим.
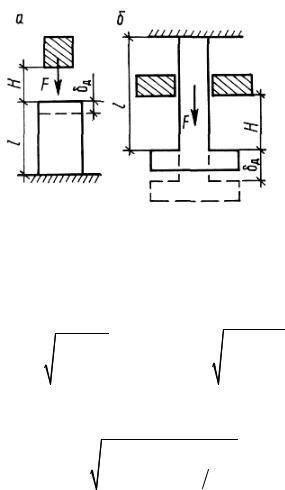
При продольном ударе принимается, что груз падает с высоты Н, ударяется о стержень и вызывает в нем сжатие или растяжение (рис. 21.1). Влияние ударного действия нагрузки на напряжения или деформации стержня оценивается коэффициентом динамичности
k = |
σд |
или k |
|
= |
δд |
, |
(21.1) |
|
|
|
д |
σст |
д |
|
δст |
|
|
|
|
|
|
|
где σст, δст – напряжение и деформация упругого стержня при статическом приложении нагрузки; σд, δд – то же, при ударном приложении нагрузки.
Рис. 21.1
Расчетная схема стержня при продольном ударе: а – сжатие; б – растяжение
Величина динамического коэффициента при продольном ударе равна
|
|
|
|
|
|
|
|
v2 |
|
k |
|
= 1+ 1+ |
2Н |
или k |
|
= 1+ 1 + |
. |
д |
|
д |
|
|
|
|
δст |
|
|
gδст |
|
|
|
|
|
|
|
При значительной массе стержня по сравнению с массой ударяюще- го тела динамический коэффициент
|
kд = 1+ 1 + |
|
2Н |
|
|
|
, |
|
δст (1 |
|
|
|
+ kQ Qг ) |
где Q – |
масса стержня; |
|
|
|
Qг – |
масса ударяющего тела; |
|
|
|
k – |
коэффициент приведения, равный 0,333 при растяжении материала. |
При поперечном ударе, например, по балке (рис. 21.2) динамический коэффициент определяется по аналогичной формуле
Рис. 21.2
где dст – статический прогиб сечения по направлению падающего груза.
Если масса балки велика по сравнению с массой подающего груза, формула для ди- намического коэффициента при падении
груза на середину балки записывается в виде
|
=1+ 1 + |
|
2Н |
kд |
|
|
. |
dст[1 |
|
|
|
+17Q 35Qг ] |
При попадании груза на середину балки или на конец консоли фор- мулы для динамического коэффициента таковы:
kд =1+ |
|
|
|
|
2Н |
|
|
|
|
; |
|
dст ×1+1 105 ×{1+ 2 1+ l 2 |
ab 2 |
|
|
|
|
|
}Q Qг |
kд |
=1+ |
|
|
2Н |
|
|
|
, |
|
|
|
|
|
|
|
|
Fl |
3 3ЕJ ×[1 + 33Q 140Q |
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
г |
|
|
|
|
где a, b – расстояния от силы F соответственно до левой и правой опор балки.
Методику расчета при ударном действии нагрузки рассмотрим на примерах.
Пример 1
Груз F падает на приваренную к стальному стержню жесткую пластинку (рис. 21.3). Площадь поперечного сечения стержня А, высота падения Н. Требуется определить наибольшее динамическое на- пряжение в стержне и насколько оно изменится, если площадь сечения стержня увеличить до А1 , а высоту
падения груза принять равной нулю.
Дано: F = 3 кН; Н = 3 см; А = 6 см2; А1 = 9 см2;
Рис. 21.3 |
|
l = 2 м. |
|
Решение. Вычисляем статическое перемещение Dlст стержня при |
статическом приложении силы F: |
|
Dl |
= |
Fl |
= |
3×103 × 2 |
= 0,5 ×10−4 м = 0,005см. |
|
2 ×1011 ×6 ×10−4 |
ст |
|
EA |
|
|
|
|
Находим значение динамического коэффициента

|
|
|
|
|
|
|
|
2 ×3×10−2 |
|
|
|
kд =1+ 1 + |
2Н |
=1 |
+ 1 |
+ |
= 35,65. |
|
Dlст |
0,5 ×10−4 |
|
|
|
|
|
|
|
|
|
Напряжение в стержне при статическом действии силы
scт |
= |
F |
= |
3 ×103 |
= 5 ×106 Па = 5 МПа. |
|
|
|
|
A 6 ×10−4 |
|
Определяем наибольшее динамическое напряжение в стержне при увеличении его площади до 9 см2. С этой целью вычисляем статическое перемещение
Dl = |
Fl |
= |
|
3×103 × 2 |
|
= 0,33 ×10−4 м = 0,0033 см. |
|
|
×1011 ×9 ×10−4 |
ст |
|
EA |
2 |
|
|
|
|
|
|
|
|
Находим динамический коэффициент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kд |
=1+ 1 + |
|
2 ×3 ×10−2 |
= 43,65. |
|
|
|
|
0,33×10−4 |
|
|
|
|
|
|
|
|
|
|
|
|
Напряжение в стержне при действии статической нагрузки |
|
scт |
= |
F |
= |
3 ×103 |
|
= 3,3 ×106 Па = 3,3 МПа. |
|
A |
9 ×10−4 |
|
|
|
|
|
|
|
|
|
Максимальное напряжение в стержне при динамической нагрузке sд = sстkд = 3,3×106 × 43,65 =1, 4405 ×108 Па =144,05 МПа.
Следовательно, при увеличении площади стержня с А до А1 , т. е. на 50 %, динамическое напряжение снизилось только на
178,25 −144,05100 =19,2 %.
178,25
Если сила приложена мгновенно (Н = 0),
kд =1+ 1+ 0 × 2 =1 +1 = 2.
Dlст
В этом случае динамическое напряжение в два раза больше, чем при статической нагрузке, т. е.
σд = σстkд = 2σст.
Пример 2
Груз падает с высоты Н на конец консоли двутавровой балки № 20 (рис. 21.4). Проверить прочность материала балки, определить перемеще- ние точки С от динамической нагрузки. Массу балки не учитывать.
Дано: F = 1,2 кН; Н = 6 см; Е = 2×105 МПа; R = 210 МПа; l = 2 м; a = 1 м.
Рис. 21.4. Расчетная схема балки
Решение. Балка подвергается действию поперечного (изгибающего) удара. Перемещение точки С при действии статической силы F может быть вычислено, например, на основе способа Верещагина или как
v = |
Fa2 |
(l + a) = |
1, 2 ×103 ×1 |
(2 +1) = |
|
3 × 2 ×1011 ×1840 ×10−8 |
ст |
3EI x |
|
|
|
|
|
= 3,26 ×10−4 м = 0,0326 см,
где Ix = 1840 см принят по ГОСТу для двутавра № 20. Динамический коэффициент
|
|
|
|
|
|
|
|
2 ×6 ×10−2 |
|
|
|
kд =1+ 1 + |
2Н |
=1 |
+ 1 + |
= 20, 21. |
|
Dvст |
0,0326 ×10−2 |
|
|
|
|
|
|
|
|
|
Вычисляем наибольшее напряжение от статической силы F. С этой целью строим эпюру изгибающих моментов (рис. 21.5).
Рис. 21.5. Эпюра моментов
Согласно этой эпюре, наибольший момент действует на опоре В. Следовательно, наибольшее напряжение в сечении В при статической на- грузке
sст |
= |
Мmax |
= |
|
1, 2 ×103 |
= 6,52 ×106 Па = 6,52 МПа, |
|
184 ×10−6 |
|
|
Wx |
|
где Wx = 184 см принимается согласно ГОСТу для двутавра № 20. Наибольшее напряжение в сечении В при динамической нагрузке
sд = sстkд = 6,52 × 20, 21 =131,8 МПа < R = 210 МПа.
294

Следовательно, прочность материала балки обеспечена.
Из этого примера можно сделать вывод о том, насколько опасными являются динамические нагрузки по сравнению со статическими. Прогиб балки в точке С
vд = vстkд = 0,0326 × 20,21 = 0,659 см.
Таким образом, при динамическом действии нагрузки прогиб балки в точке С увеличивается в 20,21 раза.
Задания для самостоятельной работы
Самостоятельно решить следующие задачи.
Задача 1
На шарнирно опертый по концам деревянный брус прямоугольного поперечного сечения 12×24 см посредине пролета l = 4 м с высоты 5 см па- дает груз 100 кг. Определить наибольшее нормальное напряжение и наи- больший прогиб бруса при изгибающем ударе в плоскости: а) наибольшей жесткости и б) наименьшей жесткости.
Задача 2
Определить высоту падения груза Р, при которой свободный конец консольной двутавровой балки в результате удара коснется неподвижной плоскости (рис. 21.6).
Рис. 21.6
ТЕМА 22
Расчет простейших статически неопределимых балок
Цель занятия: изучить методику расчета простейших статически не- определимых балок методом уравнения деформаций.
Рассмотрим методику расчета на конкретном примере.
Для балок, изображенных на рис. 22.1, а, построить эпюры изгибаю- щих моментов и поперечных сил.
RAy |
|
4 кН/м |
RB |
|
20 кН |
|
|
|
|
|
a) |
|
|
|
|
|
A |
RAx |
|
В |
3 м |
С |
MA |
10 м |
|
|
|
X=RB |
y |
|
yBx |
|
MA=10x |
|
|
|
|
x |
в) |
|
|
|
B |
|
A |
|
X |
RAy=X |
|
|
RAy=60 |
4 кН/м |
|
20 кН |
г) |
|
|
|
А |
|
В |
C |
МА=460 кНм |
|
|
yBP |
|
|
|
|
RAy=16 кН |
4 кН/м |
|
20 кН |
д) |
|
|
В |
|
|
|
А |
|
|
C |
МА=20 кНм |
|
|
RB=44 кН |
24
60
ж) 20
Эп М(кНм)
12
Рис. 22.1
1. Определим степень статической неопределимости балки.
Всего неизвестных составляющих опорных реакций четыре (RAy, RAx, MA, RB), а уравнений статики для плоской системы сил можно составить только три. Следовательно, система 1 раз статически неопределима. Для определения реакций необходимо составить дополнительное деформаци- онное уравнение.
2. Образуем основную систему из заданной путем удаления «лиш- ней» связи. Ее можно удалить либо в жесткой защемляющей опоре, заме-
нив ее шарнирно неподвижной, либо удалить правую шарнирно подвиж- ную опору, как показано на рис. 22.1, б.
Статическая эквивалентность заданной и основной систем достига- ется приложением реакции X = RB по направлению удаленной опорной связи.
Кинематическая эквивалентность заданной и основной систем дости- гается приравниванием к нулю перемещения в основной системе от совме- стного действия неизвестной реакции опоры RB = X и заданной нагрузки по направлению удаленной связи, так как в заданной системе прогиб на опоре В равен нулю.
yB = 0; yBx + yBp = 0.
Это уравнение совместности деформаций.
3. Прогиб уВх в основной системе от силы Х можно определить мето- дом начальных параметров (рис. 22.1, в).
а) Определим величину опорных реакций от действия неизвестного Х в основной системе.
∑x = 0; RAx = 0; ∑ y = 0; - RAy = x; ∑M A = 0; M A - x ×10 = 0; M A =10x.
б) Запишем формулу прогибов по методу начальных параметров
|
|
∑m (x - a )2 |
|
∑ pi (x - aip )3 |
∑qi (x - aiq )4 |
EJ z y = EJ z y0 |
+ EJ zq0 x + |
i |
im |
+ |
+ |
. |
|
2 |
|
|
|
|
6 |
24 |
В нашем примере начальные параметры EJ z y0 = 0 |
и EJ zq0 = 0, так |
как начало координат совпадает с жесткой заделкой, где прогиб и угол по-
ворота сечения равны нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) Для нашей схемы нагружения |
|
|
|
|
|
|
|
|
|
|
|
10 × x(10 - 0)2 |
|
x(10 - 0)3 |
1000x |
EJ z yBx |
= 0 + 0 + |
|
|
|
|
|
- |
|
|
|
|
= |
|
|
. |
|
|
|
2 |
|
|
|
6 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
yBx = |
1000x |
(вверх). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3EJ z |
|
|
|
|
|
|
|
|
|
4. Для определения прогиба уВР загрузим основную систему заданной |
нагрузкой (рис. 22.1, г). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) Определим величину опорных реакций |
|
|
|
|
|
∑x = 0. RAx = 0; ∑ y = 0. |
RAy - 4 ×10 - 20 = 0; |
|
RAy = 60кН. |
∑M A = 0. |
- M A + 4 ×10 ×5 + 20 ×130 = 0; |
M A = 460кНм. |
б) Определим прогиб yBP методом начальных параметров |
EJ z yBP = 0 + 0 - |
460(10 - 0)2 |
+ |
60(10 - 0)3 |
- |
4(10 - 0)4 |
= -14666,667. |
2 |
|
6 |
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yBP = -14666,667 (вниз). |
|
EJ z |
5. Решаем уравнение совместности деформаций и определяем вели- |
чину опорной реакции RB = x. |
|
1000x - 14666,667 = 0. |
3EJ z |
EJ z |
|
x = 44 кН. |
6. Строим окончательные эпюры изгибающих моментов, используя эквивалентную систему (рис. 22.1, д).
а) Определим величину опорных реакций.
∑x = 0, RAx = 0; ∑ y = 0, RAy - 4 ×10 + 44 - 20 = 0, RAy =16 кН. ∑M A = 0, - M A + 4 ×10 ×5 - 44 ×10 + 20 ×13 = 0, M A = 20кНм.
б) Запишем выражения для М и Q по участкам балки.
Участок АВ 0 ≤ x ≤ 10м
Q = 16 − 4x.
x = 0, Q = 16 кН;
x = 10 м, Q = −24 кН.
Поперечная сила на этом участке меняет знак. Значит, существует экстремум для изгибающего момента.
Q= 16 − 4x = 0.
x= 4м, M = -20 +16x - 4 x2 = -20 +16x - 2x2 ;
2
x = 0, M = −20кНм; |
|
x = 10м, |
М = −20 +160 − 200 = −60кНм; |
x = 4м, |
M max = -20 +16 × 4 - 2 × 42 =12кНм. |
|
|
|
|
|
Участок СВ |
0 ≤ x ≤ 3м |
|
|
|
20 |
Q = 20кН. |
|
|
|
кН |
|
|
|
|
|
|
M = −20x. |
|
|
|
|
С |
x = 0, |
M = 0; |
|
|
|
|
|
|
|
х |
|
x = 3м, |
М = −60кНм. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) На основании выполненных расчетов строим эпюры Q и М для данной балки (рис. 22.1, е, ж).
7. Для проверки правильности построения эпюр М и Q можно вы- полнить кинетическую проверку, определив величину прогиба над опорой В, который должен быть равен нулю.
EJ z yB |
= 0 + 0 − |
20(10 − 0)2 |
+ |
16(10 − 0)3 |
− |
4(10 − |
0)4 |
= |
2 |
|
6 |
24 |
|
|
|
|
|
|
|
= −1000 + 8000 − 5000 = 0. 3 3
Задания для самостоятельной работы
Решить самостоятельно следующие задачи.
Задача 1
Определить опорные реакции и построить эпюры М и Q для балки, изображенной на рис. 22.2.
20 кН
Рис. 22.2
Задача 2
Построить эпюры М и Q в общем виде для балки, изображенной на рис. 22.3.
q
l
Рис. 22.3
ТЕМА 23
Расчет осесимметричных тонкостенных оболочек по безмоментной теории
Цель занятия: изучить методику расчета осесимметричных тонко- стенных оболочек по безмоментной теории.
В основе расчета осесимметричных тонкостенных оболочек по без-
моментной теории лежит уравнение Лапласа
σm + σt = q , ρm ρt h
где h – толщина оболочки;
q – внутреннее давление (если давление будет снаружи, то в форму- лу оно подставляется со знаком минус);
rm, rt – радиусы кривизны оболочки (меридиональные и окружные), положительные для выпуклого сосуда и отрицательные для вогнутого.
Уравнение Лапласа содержит два неизвестных sm и st (меридиональ- ное и окружное нормальные напряжения).
Меридиональное напряжение sm определяется с использованием ме- тода сечений, а окружное st – по формуле Лапласа.
Рассекающая плоскость обычно выбирается нормальной к оси вра- щения оболочки, но стенки оболочки пересекаются по нормали к меридиану.
Рассмотрим методику расчета осесимметричных оболочек по безмо- ментной теории на конкретном примере.
Пример 1
Рассчитать по безмоментной теории стальную осесимметричную оболочку вращения (материал – Ст. 3, [s] = 100 МПа) (рис. 23.1).
Дано: q = 0, 4 МПа; a =1,8м; g =1×10−2 МН/м3 – объемный вес жид- кости.
Эпюра внутреннего давления, МПа
q = 0,4
1
a
q + γa=0,418
Рис. 23.1
Решение
1.Разбиваем оболочку вдоль ее оси на отдельные элементы (на ци- линдрическую и коническую части).
2.Находим закон распределения меридиональных sm и тангенциаль- ных (окружных) st напряжений вдоль цилиндрической и конической час- тей оболочки.










