
scherbo-sp2
.pdf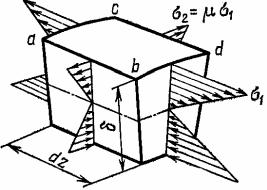
k= δE .
R2
Таким образом, дифференциальное уравнение изгиба полоски, выде- ленной из цилиндрического сосуда, можно написать как для балки, лежа- щей на сплошном упругом основании, рассмотренной ранее. Это уравнение в нашем случае примет вид
vIV + 4β4v = |
q |
. |
(18.14) |
|
E1J
Здесь величина J – момент инерции поперечного сечения полоски; при s = 1 J = δ3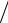 12.
12.
В выражении изгибной жесткости полоски E1J применен не обычный модуль упругости Е, а некоторая другая величина модуля E1, так как про- дольные деформации волокон полоски εl, вызванные ее изгибом, из-за взаи- модействия с соседними полосками развиваются таким образом, что соот- ветствующие поперечные деформации ε2 отсутствуют. Например, при уд- линении волокон ab и cd элемента полоски, показанного на рис. 18.13, дли- на сторон ас и bd должна остаться неизменной.
Рис. 18.13
Полагая в формулах закона Гука для плоского напряженного состоя- ния ε2 = 0, найдем, что и в этом случае связь между напряжением σ1 и удли- нением ε1 следующая:
σ1 |
= |
|
ε1E |
= ε1E1. |
|
− μ2 |
|||
|
1 |
|
||
При этом σ2 = μσ1 и распределение изгибных напряжений по граням эле- мента полоски будет таким, как оно показано на рис. 18.13. Таким образом, вместо модуля Е в этом случае надо пользоваться модулем E1 = E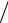 (1− μ2 ). С учетом сказанного изгибная жесткость полоски E1J составит
(1− μ2 ). С учетом сказанного изгибная жесткость полоски E1J составит
E1J = |
|
δ3E |
||
|
|
|
. |
|
12(1 |
|
|||
|
− μ2 ) |
|||
231

Величина коэффициента β в уравнении (18.14) с учетом найденных выражений для k и EJl
β = 4 |
|
k |
|
= 4 |
3(1− μ2 ) |
. |
(18.15) |
|
4E1J |
R2δ2 |
|||||||
|
|
|
|
|
|
Предположим теперь, что в поперечных сечениях трубы действуют продольные усилия, характеризуемые равномерно распределенными на- пряжениями σm. Относительное удлинение в окружном направлении в этом случае определяется равенством
et = v = σt - m σm .
R E E
Отсюда найдем st, а после этого выразим Т:
T = st d ×1 = δE v + mdsm.
R
По формуле (18.12) определим
r= δE v + μδσm .
R2 R
Последнее слагаемое здесь можно рассматривать как равномерно рас- пределенную нагрузку на балку-полоску, которую надо добавить со знаком минус к внешней нагрузке q. Появление ее легко понять, если учесть, что растяжение трубы в продольном направлении с напряжениями sm сопрово- ждается ее сужением. Это, как видим, эквивалентно приложению отрица- тельного давления (μδσm )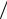 R . Следовательно, с учетом продольных напря-
R . Следовательно, с учетом продольных напря-
жений sm уравнение изгиба полоски получит вид
|
1 |
|
μδσ |
|
|
vIV + 4β4v = |
|
q − |
|
m . |
(18.16) |
|
|
||||
|
E1J |
R |
|
|
|
Заметим, что уравнения (18.14) и (18.16) справедливы для произвольной осесимметричной нагрузки q. Вернемся к решению нашей задачи для случая q = const и σm = 0. Общий интеграл уравнения (20.14) запишется в виде
v = e−βz (C sin bz + C |
2 |
cosbz) + |
|
||
|
1 |
|
(18.17) |
||
+eβz (C sin bz + C cosbz) + q (4b4 E J ). |
|||||
|
|||||
3 |
4 |
|
1 |
|
|
По физическому смыслу задачи с возрастанием z величина v должна стремиться к определенному значению. В решении (18.17) этому противоре- чит то обстоятельство, что при z ® ¥ величина еβz также стремится к беско- нечности. Поэтому полагаем С3 = С4 = 0. Две другие постоянные С1 и С2 най-
дем из условия, что у фланца, т. е. при z = 0 |
|
dv |
= 0 и v = 0. Это дает |
|||||
|
|
|||||||
|
|
|
|
|
dz |
|||
C = C |
|
= − |
q |
= − |
qR2 |
|
||
2 |
|
δE |
||||||
1 |
|
4β4 E1J |
|
|
|
|||
|
|
|
|
|
|
|||
232
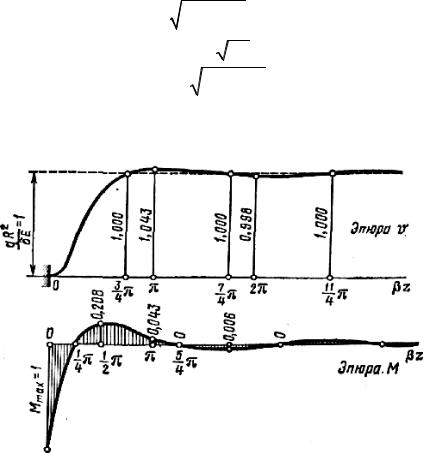
и
v = |
qR2 |
1− e−βz |
(sin βz + cosβz) . |
(18.18) |
|
δE |
|||||
|
|
|
|
Теперь легко найдем изгибающий момент М и поперечную силу Q для полоски шириной s = 1:
M = E J |
d 2v |
= |
|
|
|
qRδ |
e−βz (cosβz − sin βz); |
(18.19) |
|||||||
|
|
|
|
|
|
|
|
|
|||||||
1 |
dz2 |
2 3(1 − μ2 ) |
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
q |
|
|
|
|
|
||||||
Q = |
dM |
= − |
Rδ |
|
|
e−βz cosβz. |
(18.20) |
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
dz |
|
|
4 3(1 − μ2 ) |
|
|||||||||
Эпюры v и М, построенные по (18.18) и (18.19), показаны на рис. 18.14, где по оси абсцисс отложена безразмерная координата βz.
Рис. 18.14
Путем сопоставления можно заметить, что величины v, M и Q в нашем случае выражаются через функции η, η1 и η2, с помощью которых в М-9, п. 9.6 определялись прогибы, моменты и поперечные силы бесконечно длин- ной балки на упругом основании при действии одной сосредоточенной си- лы. Это совпадение не случайно. Нетрудно видеть, что нашу задачу можно трактовать как задачу об изгибе полоски, выделенной из трубы, как балки на упругом основании под действием сосредоточенной силы. Этой силой, очевидно, является реакция фланцев.
Из эпюр на рис. 18.14 можно видеть, что ординаты изгибной дефор- мации стенок трубы с удалением от фланца быстро уменьшаются. Так, при βz = π величина прогиба v лишь на 4,3 % отличается от значения
233

(qR2 )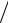 (δE), представляющего собой увеличение радиуса трубы при ее сво-
(δE), представляющего собой увеличение радиуса трубы при ее сво-
бодном расширении и при отсутствии фланца. В этом же сечении изгибаю- щий момент составляет также 4,3 % от наибольшего момента у фланца. Значению βz = π соответствует (при μ = 0,3 )
z = |
π |
= |
|
π |
Rδ |
|
|
≈ 2, 4 |
|
. |
|
|
|
|
Rδ |
||||||||
β |
|
|
|
|
|
||||||
4 3(1− μ2 ) |
|||||||||||
|
|
|
|
|
|
||||||
Например, при δ = 0,1R z ≈ 0,76R. Таким образом, в этом случае с точностью до 5 % можно считать, что краевой эффект распространяется от фланца лишь на длину, меньшую радиуса трубы. Вследствие резко выра- женного местного проявления изгиба стенок это явление и называют крае-
вым эффектом.
Максимальное напряжение вследствие краевого эффекта может достигать весьма больших величин. Так, в нашем случае при z = 0 имеем:
|
|
M max = |
|
|
qRδ |
|
; |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
3(1 − μ2 ) |
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|||||
σmax |
= |
6M max |
= |
|
|
|
3qR |
|
≈ 1,82 |
qR |
, |
||
δ2 |
|
|
|
|
|
|
|
δ |
|||||
δ |
3(1 − μ2 ) |
|
|||||||||||
|
|
|
|
|
|
||||||||
что (при μ = 0,3) в 1,82 раза больше максимального напряжения, опреде- ляемого безмоментной теорией по формуле (18.4).
Если материал оболочки пластичный, например, пластичная сталь, то повышение напряжений из-за краевого эффекта не снижает общей прочно- сти сосуда, а может привести лишь к местным пластическим деформациям.
Значительно более опасными являются напряжения от краевого эф- фекта для хрупких материалов, например, для железобетонных резервуаров, где указанные напряжения могут привести к появлению трещин и, как след- ствие, к нарушению непроницаемости резервуара. В этом случае с напряже- ниями краевого эффекта борются с помощью различных конструктивных мер. Одна из них – создание предварительных напряжений сжатия в стенках железобетонного резервуара. Иногда применяют такую конструкцию со- единения стенок резервуара и днища, которая допускает полностью или частично свободное расширение стенок. Это резко снижает или совсем уст- раняет напряжения краевого эффекта.
234
РУКОВОДСТВО К ПРАКТИЧЕСКИМ
ЗАНЯТИЯМ
235

ТЕМА 10
Косой изгиб
Цель занятия: изучить методику расчета брусьев на косой изгиб.
Напряжение в любой точке поперечного сечения определяется по формуле
s = |
M |
z |
y + |
M y |
z |
|
|
|
|||
|
J z |
Je |
|
||
В поперечных сечениях с двумя осями симметрии и угловыми точ- ками всегда найдется точка, где будут действовать максимальные нор- мальные напряжения, и условие прочности при расчете по допускаемым напряжениям имеет вид
M z + M y ≤ [σ].
Wz Wy
При расчете по предельным состояниям вместо допускаемого на- пряжения будет расчетное сопротивление R, только Mz и Му вызываются действием расчетных нагрузок.
Для произвольных поперечных сечений необходимо определить по- ложение нейтральной оси. Опасными будут точки, находящиеся на наи- большем удалении от нейтральной оси.
Положение нейтральной оси определяется углом наклона b ней- тральной оси к главной центральной оси z.
tgb = tga × J z ,
J y
где a – угол наклона между вертикальной главной центральной осью и следом плоскости действия суммарного изгибающего момента.
След плоскости действия суммарного изгибающего момента проходит через квадранты, где находятся точки с максимальными нормальными на- пряжениями, а нейтральная ось никогда не проходит через эти квадранты.
Рассмотрим пример расчета стержней на косой изгиб.
Пример 1
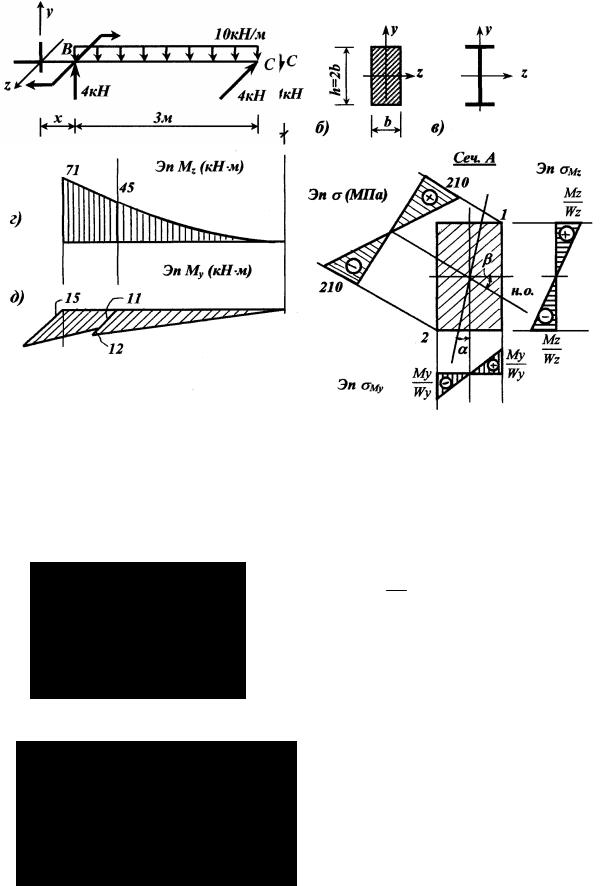
Определить размеры поперечных сечений стальной балки, найти по- ложение нейтральной оси и построить эпюру нормальных напряжений в опасном прямоугольном сечении для балки, изображенной на рис. 10.1, принять R = 210 МПа , а нагрузки – расчетными.
236
е)
Рис. 10.1
Запишем выражения для Mz и My по участкам балки и вычислим их значения для характерных сечений
Участок СВ 0 ≤ х ≤ 3 м
Мz = −10 x2 = −5x2. 2
x = 0, M z = 0; x = 3 м, Мz = -45 кНм
М у = -4х.
х = 0, М у = 0; х = 3 м, М у = -12 кНм
Участок ВА 0 ≤ х ≤ 1 м
Мz = -10 ×3(1,5 + х) + 4х = -45 - 26х. x = 0, M z = −45 кНм;
х = 1 м, M z = −71 кНм.
М у = -4(3 + х) +1 = -11 - 4х; х = 0, М у = −11 кНм; х = 1 м, М у = −15 кНм.
237
1.На основании выполненных расчетов строим эпюры Мz и Mу
(рис. 10.1, г, д).
2.Анализируем эпюры Мz и Mу и устанавливаем, что наиболее опас- ным сечением является сечение А у жесткой заделки, где Мz и Mу имеют максимальные по абсолютной величине значения, а опасными точками (см. рис. 10.1, е) являются точки 1 и 2. В точке 1 будут наибольшие растя- гивающие, а в точке 2 – наибольшие сжимающие напряжения. На сечение смотрим по направлению оси х.
3.Определим положение нейтральной оси. След плоскости действия
результирующего изгибающего момента определяется углом α и проходит через 1-й и 3-й квадранты.
|
|
|
M y |
|
|
15 |
|
|
||
|
|
|
|
|
|
|||||
tga |
= |
|
|
|
= |
|
|
= 0,2113; |
a = arctg0,2113 »12 . |
|
M z |
71 |
|||||||||
|
|
|
|
|
|
|
||||
Положение нейтральной оси определяется
|
|
|
|
|
|
tgb |
|
= |
|
tga |
|
|
J z |
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
J z |
= |
bh3 |
= |
b(2b)3 |
= |
2 |
b4 ; J y |
|
= |
hb3 |
= |
2b ×b3 |
= |
1 |
b4 ; |
|||||||
|
|
|
|
|
|
|
||||||||||||||||
|
12 |
12 |
|
3 |
|
|
|
|
|
12 |
12 |
6 |
|
|||||||||
tgb = 0,2113 × 2b4 ×6 = 0,2113 × 4 = 0,8452 ; 3×b4
b = arctg0,8452 » 39 .
4. Определим из условия прочности по предельным состояниям ве- личину размеров прямоугольного поперечного сечения.
Наиболее опасные точки 1 и 2, но для материалов, одинаково сопротив- ляющихся растяжению и сжатию, они равноопасны. Остановимся на точке 1.
smax = s1 = M z + M y £ R.
Wz Wy
Для прямоугольного поперечного сечения моменты сопротивления будут равны:
Wz |
= |
bh2 |
= |
b(2b)2 |
= |
2 |
b3; Wy = |
hb2 |
= |
2b ×b2 |
= |
1 |
b3. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
6 |
|
|
6 |
|
3 |
|
|
6 |
|
|
6 |
3 |
|||||||||||||
|
|
|
3M |
z |
|
3M y |
|
|
|
|
1,5M |
z |
|
|
|
|
3M y |
|
|
|
|
|||||
|
|
|
|
|
+ |
|
|
£ R; |
|
+ |
|
|
|
|
|
£ R. |
|
|
|
|||||||
|
|
|
|
|
|
b3 |
b3 |
|
|
|
b3 |
|
|
|
||||||||||||
|
|
|
2b3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
b = |
3 |
1,5M z + 3M y |
; |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мz |
= 71 кН×м = 7100 кН×см. |
|
|
|
|||||||||||||||||
|
|
|
|
|
M y =15 кН×м =1500 кН×см . |
|
|
|
||||||||||||||||||
238

R = 210 МПа = 21 кНсм2 ;
b = 3 1,5 ×7100 + 3 ×1500 = 8,98 см » 9 см.
1,5 ×7100 + 3 ×1500 = 8,98 см » 9 см.
21
h = 2b = 18 см .
5. Определим требуемый номер двутавровой балки.
Предварительно необходимо задаться соотношением
Для средних номеров двутавра Wy »10.
|
|
|
|
|
Wz |
|
|
|
|
|
M |
z |
+ |
M y |
£ R; |
|
M |
z |
+ |
M y |
£ R; |
|
|
|
|
|
|
0,1Wz |
||||
Wz |
Wy |
|
|
Wz |
|
|||||
Wy . Wz
Wz ³ M z +10M y = 7100 +10 ×1500 =1052,4 см3. R 21
Обращаемся к сортаменту прокатной стали и выбираем номер дву- тавра с близким к требуемому моменту сопротивления. Наиболее близко
подходит двутавр № 45 с Wz |
=1231 |
см3 и Wy =101 cм3. |
|
|
|
|||||||||||
Проверим подобранный двутавр |
|
|
|
|
||||||||||||
smax = |
M |
z |
+ |
M y |
= |
7100 |
+ |
1500 |
= 5,768 |
+14,851 = 20,619 |
кН |
|
2 = |
|||
W |
|
W |
y |
1231 |
|
101 |
|
см |
||||||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|||
= 206,19 МПа £ R = 210 МПа.
Прочность обеспечена. Окончательно выбираем к установке двутавр № 45.
Задания для самостоятельной работы
Решить самостоятельно следующие задачи.
Задача 1
Шарнирно опертая по концам балка длиной 4 м несет равномерно распределен- ную нагрузку интенсивностью q = 5 кН/м.
Поперечное сечение балки – швеллер № 18. |
|
Стенка швеллера наклонена к плоскости дей- |
|
ствия нагрузки под углом j = 5 (рис. 10.2). |
|
Определить нормальные напряжения в точ- |
|
ках А, В, С и D опасного сечения балки и |
|
построить эпюру нормальных напряжений. |
Рис. 10.2 |
239
Задача 2
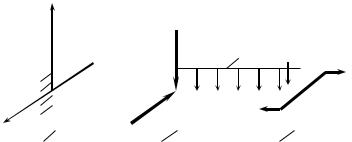
Двутавровая стальная балка нагружена нагрузкой в вертикальной и горизонтальной плоскостях, как показано на рис. 10.3.
Подобрать необходимый номер двутавровой балки. Нагрузки счи- тать расчетными, а расчетное сопротивление принять равным
R = 210 МПа.
y
4 кН
2 кН/м 2 кН×м
z |
|
|
|
|
|
4 кН |
|
|
|
|
|
|
||
|
|
|
||
|
|
|
|
|
|
|
2 м |
|
2 м |
|
|
|||
|
|
|
|
|
|
|
|
|
|
Рис. 10.3
ТЕМА 11
Внецентренное растяжение (сжатие)
Цель занятия: изучить методику расчета брусьев на внецентренное растяжение (сжатие).
Напряжение в любой точке поперечного сечения при внецентренном сжатии
s = |
F |
+ |
z |
F |
× z |
+ |
y |
F |
× y |
||
|
1 |
|
|
|
|
, |
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|
2 |
||
|
A |
|
|
iy |
|
|
iz |
|
|
||
где zF, yF – координаты приложения нагрузки в системе главных цен- тральных осей поперечного сечения;
z, y – координаты рассматриваемой точки в системе главных центральных осей поперечного сечения;
А – площадь поперечного сечения;
iz2 , iy2 – квадраты радиусов инерции сечения относительно главных
центральных осей.
При растягивающей нагрузке значение F берется с плюсом, а при сжимающей – с минусом.
Для определения опасных точек находят положение нейтральной оси. Отрезки, отсекаемые нейтральной осью на главных центральных осях, равны:
240
